 微分積分学(大学)
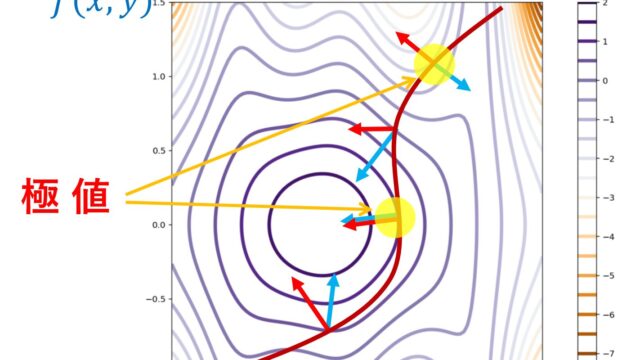
微分積分学(大学) ラグランジュの未定乗数法とは~意味と証明~
ラグランジュの未定乗数法 (Lagrange multiplier) は,多変数関数における,条件付き極値問題を解く方法を指します。これについて,その内容とイメージ,証明を解説しましょう。
 微分積分学(大学)
微分積分学(大学) 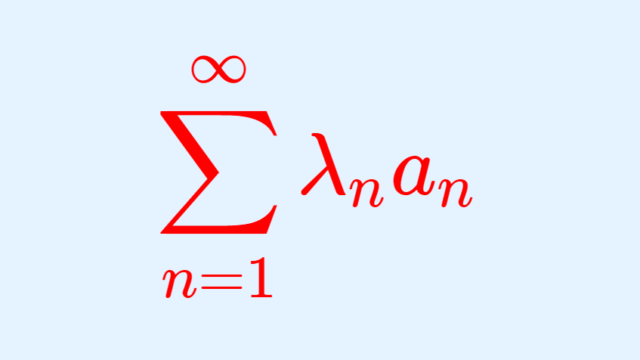 微分積分学(大学)
微分積分学(大学) 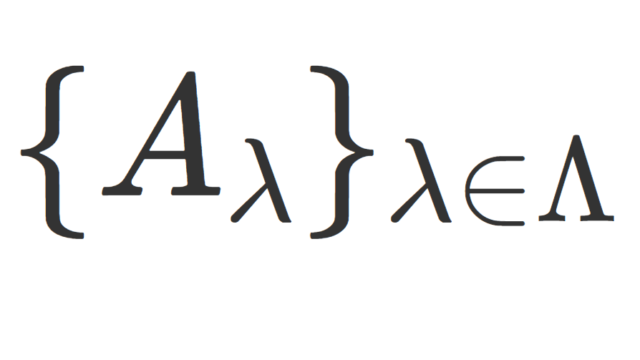 集合と位相
集合と位相 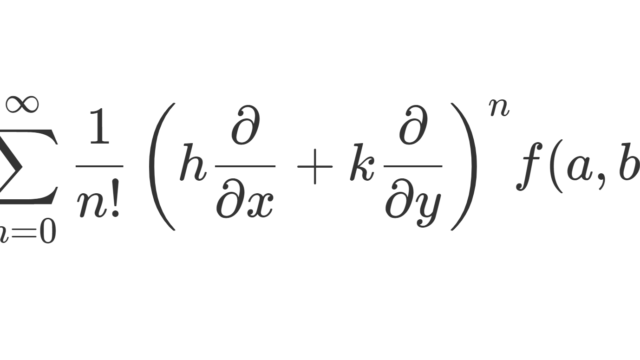 微分積分学(大学)
微分積分学(大学) 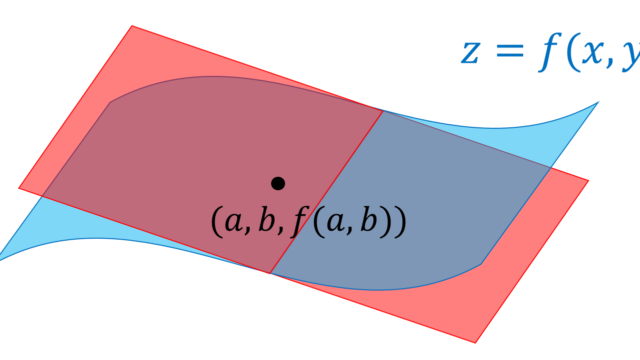 微分積分学(大学)
微分積分学(大学)  集合と位相
集合と位相  集合と位相
集合と位相  解析学(大学)その他
解析学(大学)その他  集合と位相
集合と位相  微分積分学(大学)
微分積分学(大学)