確率論 負の二項分布の積率母関数(モーメント母関数)・特性関数とその導出
負の二項分布NB(r, p)における，積率母関数(モーメント母関数)・特性関数をそれぞれ提示し，それの導出ついての証明をおこないましょう。
解析学(大学)
確率論 
確率論 負の二項分布の定義と例と性質まとめ
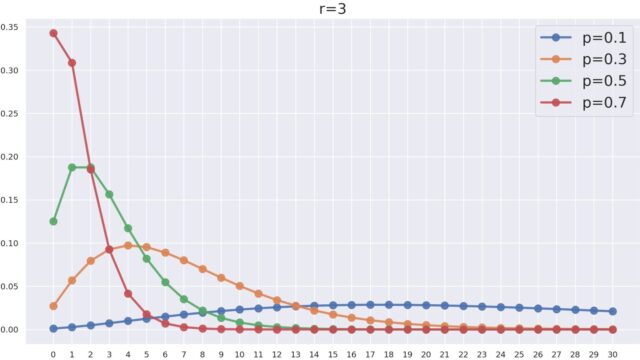
コイン投げをしたときの失敗回数を固定し，その失敗回数に到達するまでの成功回数を数える負の二項分布NB(r, p) (negative binomial distribution) について，その定義と例と性質をまとめましょう。
確率論 マルコフの不等式とその証明をわかりやすく厳密に
確率変数に対する不等式P(|X|≧a) ≦ E[|X|]/aをマルコフの不等式 (Markov's inequality) といいます。これについて，分かりやすくかつ厳密に証明しましょう。最後には，一般の測度論に関するマルコフの不等式を紹介します。
確率論 正規分布の標準化とその証明
X ~ N(μ, σ^2)のとき，Z = (X-μ)/σ とスケール変換すると，Z ~ N(0,1)になります。これを，正規分布の標準化 (standardization) といいます。これについて，詳しく述べ，証明しましょう。
確率論 正規分布の歪度・尖度とその導出証明
正規分布の歪度(わいど, skewness)・尖度(せんど, kurtosis)は，両方とも0になります。これについて，その導出の証明を行いましょう。
確率論 正規分布の再生性とその詳しい証明
正規分布の再生性 (reproductive property) について，和の再生性と定数倍の再生性に分けて，それぞれを確率密度関数や特性関数を用いて証明しましょう。
確率論 正規分布の期待値(平均)・分散・標準偏差とその導出証明
正規分布の期待値(平均)・分散・標準偏差について，その導出の証明を行います。「定義から直接証明する方法」と「特性関数の微分を用いた方法」の2通りで証明しましょう。
確率論 正規分布の積率母関数(モーメント母関数)・特性関数とその導出証明
正規分布の積率母関数(モーメント母関数)・特性関数について，その導出の証明を行いましょう。
確率論 正規分布の定義と性質まとめ
正規分布 (normal distribution)，またはガウス分布 (Gaussian distribution) は，確率論や統計学において，最も基本的な連続型の分布だといえます。この分布について，定義と性質を分かりやすくまとめることにしましょう。
確率論 ポアソン分布の再生性とその2通りの証明
ポアソン分布には，「再生性 (reproductive property)」と呼ばれる性質があります。この性質について，その証明を，「定義から直接証明」「特性関数を用いた証明」の2通りで行いましょう。