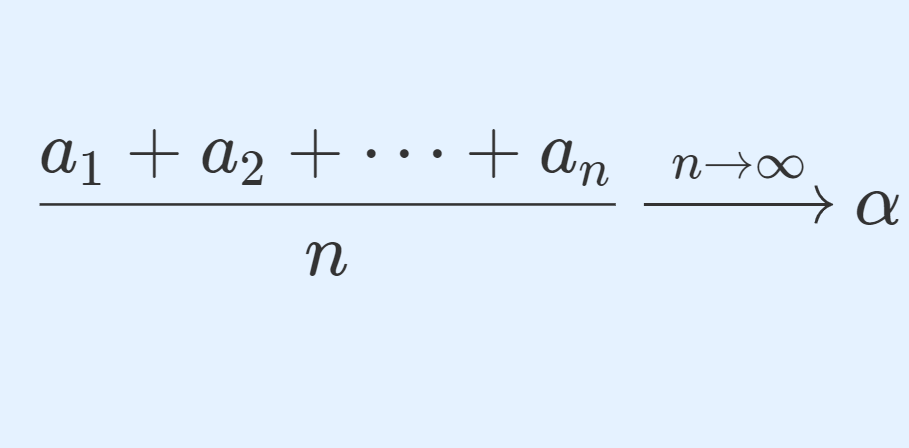PR

【チェザロ平均】数列が収束するとき平均も同じ値に収束する証明

2021.02.27
微分積分学(大学)
大学教養
記事内に広告が含まれています。

数列の極限を定義する，イプシロンエヌ論法を習った後によく出てくる有名な定理の一つとして，「数列が収束すれば平均も同じ値に収束する」というものがあります。これについて紹介します。

【チェザロ平均】数列が収束するとき平均も同じ値に収束する

定理1（数列の平均の収束）

数列 {an} \{a_n\} が an→n→∞α∈[−∞,∞] a_n \xrightarrow{n\to\infty} \alpha \in [-\infty, \infty] をみたすとする。このとき，その平均について

a1+a2+⋯+ann→n→∞α \frac{a_1 + a_2 + \cdots + a_n}{n} \xrightarrow{n\to\infty} \alpha


となる。

ここで，

1n∑k=1nak=a1+a2+⋯+ann \frac{1}{n} \sum_{k=1}^n a_k = \frac{a_1 + a_2 + \cdots + a_n}{n}


をチェザロ平均 (Cesàro mean) といいます。

【チェザロ平均】定理の証明

証明は −∞<α<∞ -\infty < \alpha < \infty のときと，α=±∞ \alpha = \pm \infty のときで分けて行うことにします。

-∞ < α < ∞ のとき

証明；−∞<α<∞ -\infty < \alpha < \infty のとき

ε>0 \varepsilon > 0 とする。
an→α  (n→∞) a_n \to \alpha \,\,(n\to\infty) より，ある N0≥1 N_0 \ge 1 が存在して，

n≥N0  ⟹  ∣an−α∣<ε n\ge N_0 \implies |a_n - \alpha| < \varepsilon


が成立する。また，収束列は有界なので ∣an∣<M  (n≥1) |a_n| < M \,\,(n\ge 1) となる M>0 M>0 が取れる(→ 収束する数列は有界であることの証明)。
ここで，N=max⁡{N0,N0(M+∣α∣)/ε} N = \max\{N_0, N_0(M+|\alpha|) /\varepsilon\} と定めよう。このとき，n≥N n \ge N ならば，

∣1n∑k=1nak−α∣=∣1n∑k=1n(ak−α)∣≤1n∑k=1n∣ak−α∣=1n∑k=1N0∣ak−α∣+1n∑k=N0+1n∣ak−α∣≤N0n(M+∣α∣)+n−N0nε≤ε+ε=2ε \begin{aligned} &\left| \frac{1}{n} \sum_{k=1}^n a_k - \alpha \right| \\ &= \left| \frac{1}{n} \sum_{k=1}^n (a_k - \alpha) \right| \\ &\le \frac{1}{n} \sum_{k=1}^n |a_k - \alpha | \\ &= \frac{1}{n} \sum_{k=1}^{N_0} |a_k - \alpha | + \frac{1}{n} \sum_{k=N_0+1}^n |a_k - \alpha | \\ &\le \frac{N_0}{n}(M + |\alpha|) + \frac{n-N_0}{n} \varepsilon \\ &\le \varepsilon + \varepsilon = 2\varepsilon \end{aligned}


であるから，1n∑k=1nak→n→∞α \frac{1}{n} \sum_{k=1}^n a_k \xrightarrow{n\to\infty}\alpha を得る。

証明終

V = ±∞ のとき

証明；α=±∞ \alpha = \pm\infty のとき

α=∞ \alpha = \infty として証明する。

M>0 M > 0 とする。
an→∞  (n→∞) a_n \to \infty \,\,(n\to\infty) より，ある N0≥1 N_0 \ge 1 が存在して，

n≥N0  ⟹  an>M n\ge N_0 \implies a_n > M


が成立する。また，下に有界なので an>−L  (n≥1) a_n > -L\,\,(n\ge 1) となる L>0 L > 0 が取れる。
ここで，N=max⁡{2N0,4N0L/M} N = \max\{2N_0,4N_0L/M\} と定めよう。このとき，n≥N n \ge N ならば，

1n∑k=1nak=1n∑k=1N0ak+1n∑k=N0+1nak≥−N0nL+n−N0nM≥−14M+12M=14M \begin{aligned} &\frac{1}{n} \sum_{k=1}^n a_k \\ &= \frac{1}{n} \sum_{k=1}^{N_0} a_k + \frac{1}{n} \sum_{k=N_0+1}^n a_k \\ &\ge -\frac{N_0}{n}L + \frac{n-N_0}{n}M \\ &\ge -\frac{1}{4} M + \frac{1}{2} M = \frac{1}{4}M \end{aligned}


であるから，1n∑k=1nak→n→∞∞ \frac{1}{n} \sum_{k=1}^n a_k \xrightarrow{n\to\infty}\infty を得る

証明終

類似の定理～相乗平均の収束～

上の定理は特に「相加平均」(あるいは「算術平均」)と呼ばれる平均に関するものでした。これは「相乗平均」(あるいは「幾何平均」)に関しても同じ事が成立します。

定理2（数列の相乗平均の収束）

数列 {an} \{a_n\} が an>0,≥an→n→∞α∈[0,∞] a_n >0 , \ge a_n \xrightarrow{n\to\infty} \alpha \in [0, \infty] をみたすとする。このとき，その相乗平均について

a1a2a3⋯ann→n→∞α\sqrt[n]{a_1a_2a_3\cdots a_n} \xrightarrow{n\to\infty} \alpha


となる。

証明については，対数 (log⁡ \log ) をとって相加平均に帰着させることで，同様です。

逆は成り立たない

an→α  ⟹  a1+a2+⋯+ann→α a_n \to \alpha \implies \dfrac{a_1+a_2+\cdots + a_n}{n} \to \alpha は成立しますが，その逆は一般には成立しません。たとえば，

{(−1)n+1} \{(-1)^{n+1}\}


は振動しますが，その平均は 0 0 に収束します。

「収束の基本的なこと」に関する他の話題