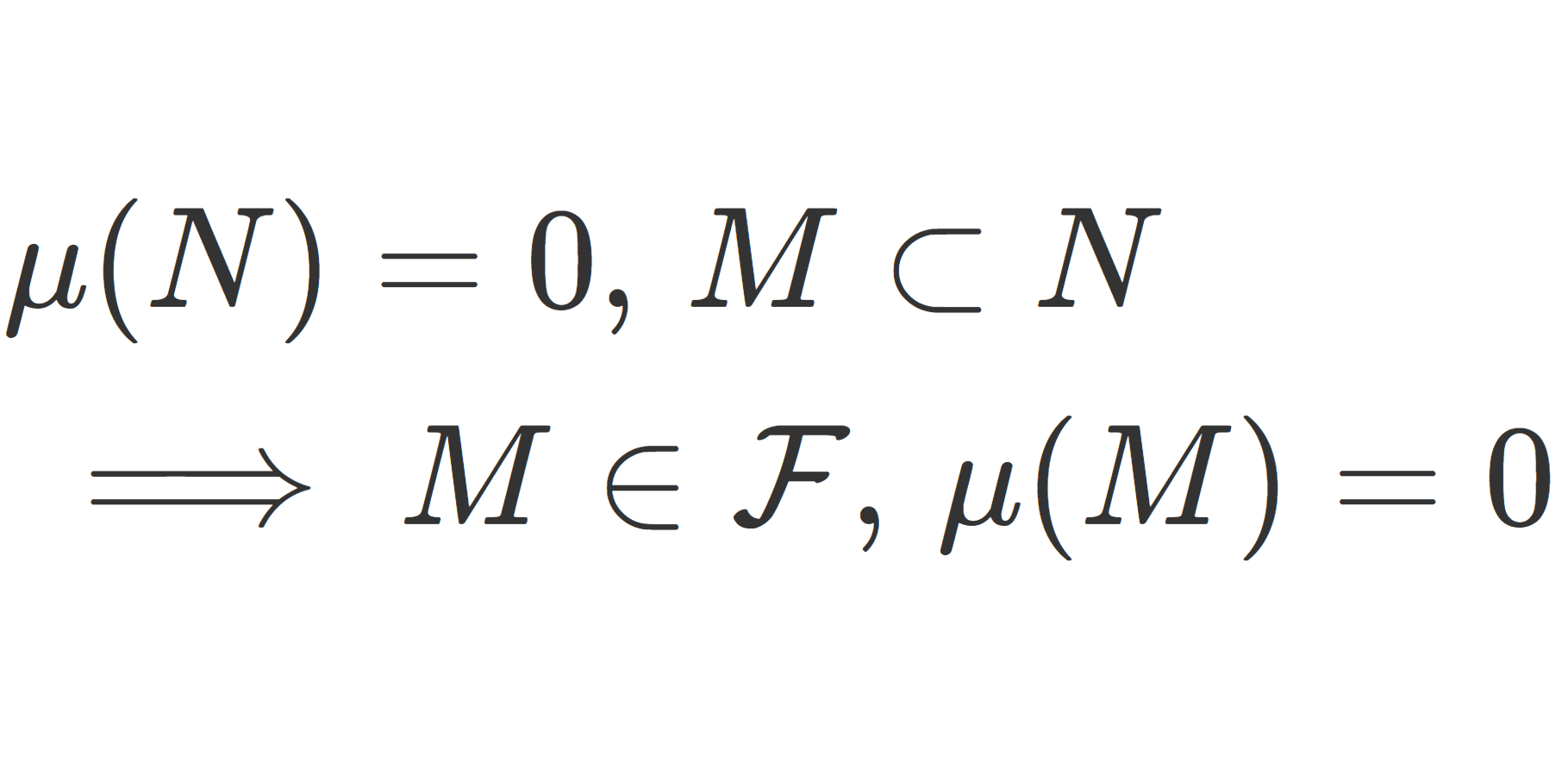完備な測度空間とは,零集合の任意の部分集合が可測,従って零集合になる測度空間のことをいいます。任意の測度空間は完備な拡張を持つことが知られています。
完備な測度と,任意の測度空間の完備化について紹介しましょう。
完備測度空間
定義(完備測度空間)
測度空間 (X, \mathcal{F},\mu) が完備 (complete) であるとは, N\in\mathcal{F} が \mu(N)=0 をみたすとき, N の任意の部分集合が \mathcal{F} に属することをいう。
N\in\mathcal{F},\, \mu(N)=0 かつ M\subset N なら M\in \mathcal{F} ということです。このとき,当然 \mu(M)=0 ですから, 完備測度空間とは,任意の零集合の部分集合が零集合になる測度空間といっても構いません。 A が零集合とは, A\in \mathcal{F} かつ \mu(A)=0 となることを指します。
(X, \mathcal{F},\mu) が完備であることを,単に \mu が完備 (complete) であるということもあります。
具体例を挙げましょう。
例1.
X を,要素を2つ以上持つ集合とし,測度空間 (X, \{\emptyset, X\}, \mu) に対し,
- \mu(X)>0 とすると,これは完備である。
- \mu(X)=0 とすると,これは完備でない。
\mu(X)=0 とすると, X の部分集合も可測集合にならなければならないので,完備ではありません。
例2.
任意の測度空間 (X,2^X, \mu) は完備である。ただし, 2^X はべき集合を意味する。
X の全ての部分集合が可測になる空間は,当然完備です。
測度空間の完備化
2つの測度空間 (X, \mathcal{F}_1, \mu_1) と (X,\mathcal{F}_2,\mu_2) について, \mathcal{F}_1\subset \mathcal{F}_2 かつ, \mu_2|_{\mathcal{F}_1}=\mu_1 となるとき,測度空間 (X,\mathcal{F}_2, \mu_2) は (X, \mathcal{F}_1, \mu_1) の拡張 (extension) であるといいます。
今から考えたいのは,測度空間 (X, \mathcal{F}, \mu) の完備拡張です。
定理(測度空間の完備化)
測度空間 (X,\mathcal{F},\mu) の最小の完備拡張 (X,\mathcal{F}^*,\mu^*) が一意に存在する。すなわち,
- (X,\mathcal{F}^*,\mu^*) は完備であり,かつ元の空間の拡張である。
- (X,\mathcal{F}',\mu') を別の完備拡張とするとき, (X,\mathcal{F}^*,\mu^*) の拡張にもなっている
このとき, (X,\mathcal{F}^*,\mu^*) を,元の測度空間の完備化 (completion) という。
単に測度 \mu^* を \mu の完備化 (completion) ともいいます。
ちょっと手抜きですが,軽く証明しておきましょう。
証明
\begin{aligned}\mathcal{N}&=\{ N\in\mathcal{F}\mid \mu(N)=0\}, \\ \mathcal{N}^* &= \{ N^*\subset N\mid N\in\mathcal{F}\}, \\ \mathcal{F}^* &= \{ A\cup N^* \mid A\in\mathcal{F}, N^* \in \mathcal{N}^*\}\end{aligned}
と定める。 \mathcal{F}^* がσ加法族であることは簡単な演習である。 A^*= A\cup N^* \in \mathcal{F}^* に対し,
と定める。もし, A^*=A_1\cup N_1^*=A_2\cup N_2^* と2通りの表現があったとすると, N_1^*\cup N_2^* \subset N となる N\in\mathcal{N} を取ることで,
となるから, (1) 式はwell-definedである。 \mu^* が \mathcal{F}^* 上の測度になることは,簡単な演習である。
最小性について示そう。 (X,\mathcal{F}',\mu') を別の完備拡張とする。完備の定義より, N^*\subset \mathcal{F}' であるから, \mathcal{F}^*\subset \mathcal{F}' である。また,A^*=A\cup N^* \in\mathcal{F}^* のとき,
\begin{aligned} \mu'(A^*)&=\mu'(A) +\mu'(N^*\setminus A) \\&= \mu(A)=\mu^*(A^*) \end{aligned}
であるから, (X,\mathcal{F}',\mu') は (X,\mathcal{F}^*,\mu^*) の拡張でもある。一意性は最小性よりよい。
証明終
対称差を A\triangle A^* = (A\setminus A^*)\cup (A^*\setminus A) と定めると,上式の \mathcal{F}^* は
\mathcal{F}^*= \{A^*\subset X\mid \exists A\in \mathcal{F}, A\triangle A^*\in \mathcal{N}\}
ともかけます。
測度の完備化の例1.
(\R, 2^{\mathbb{Q}\cup \{\R\setminus \mathbb{Q}\}} , \#_\mathbb{Q}) を,有理数の数を数える数え上げ測度 (counting measure) が定まった空間とする。ただし,
2^{\mathbb{Q}\cup \{\R\setminus \mathbb{Q}\}}=\left\{A\cup B\middle|\begin{gathered} A\subset\mathbb{Q}, \\ B=\emptyset \text{ or } \R\setminus \mathbb{Q}\end{gathered}\right\}
の意味とする。 \#_\mathbb{Q} の例としては,たとえば
である。このとき,この測度空間の完備化は (\R, 2^\R, \#_{\mathbb{Q}}) である。
\#_\mathbb{Q}(\R\setminus\mathbb{Q})=0 ですから,無理数の集合 \R\setminus\mathbb{Q} の任意の部分集合が零集合になるように,測度空間が拡張されます。
測度の完備化の例2.
\R 上のボレル測度 (Borel measure) を完備化したものが,ルベーグ測度 (Lebesgue measure) である。
測度空間を完備化することで,可測集合が増えるわけですから,「常に測度空間は完備化しておけばよいじゃん」と思うかもしれませんが,そんなことはありません。完備化という概念は測度に依存するため,たとえば一つの可測空間 (X,\mathcal{F}) の上に異なる複数の測度を考えたい場合は,適さない場合もあるのです。