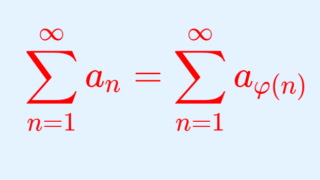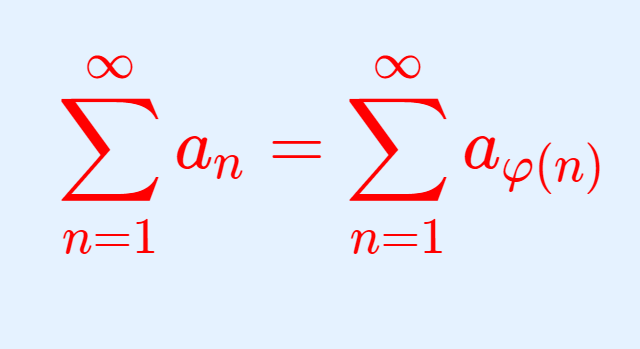PR

条件収束級数は和の順序交換により任意の値に収束できることの証明

2021.02.26
微分積分学(大学)
大学教養
記事内に広告が含まれています。

有限和においては，a1+a2+a3=a3+a1+a2 a_1 + a_2 + a_3 = a_3 + a_1 + a_2 のように，和の順序を交換しても同じ値に収束します。一方でこれは無限和では成立しません。単に成立しないどころか，「和の順序を変えることで任意の値に収束できる」ことがあります。今回はこのような定理を紹介・証明します。

リーマンの再配列定理

定理 (リーマン; Riemann)

実数列 {an} \{a_n\} の和が条件収束する，すなわち ∑n=1∞an \sum_{n=1}^\infty a_n は収束するが，∑n=1∞∣an∣=∞ \sum_{n=1}^\infty |a_n| = \infty (絶対収束しない)とする。
このとき，この数列の和は順序を交換することで，任意の実数または ±∞ \pm \infty に収束させることができる。

すなわち，任意の V∈[−∞,∞] V \in [-\infty, \infty] に対して，正の整数の間のある全単射 φ ⁣:Z≥1→Z≥1 \varphi \colon \mathbb{Z}_{\ge 1} \to \mathbb{Z}_{\ge 1} が存在して，

∑n=1∞aφ(n)=V \textcolor{red}{\sum_{n=1}^\infty a_{\varphi(n)} = V}

とできる。

条件収束する級数は，たとえば，

∑n=1∞(−1)n+1n=1−12+13−14+⋯\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} = 1 - \frac{1}{2}+ \frac{1}{3} - \frac{1}{4} + \cdots

のようなものが挙げられます(この収束値は log⁡2 \log 2 になります)。

証明に入る前に準備として，以下の条件収束に関する性質を挙げ，それを証明したいと思います。

証明の準備

定理を証明するために使う，以下の補題を証明しましょう。補題とは，定理を支えるための定理(命題)です（→ 定義・公理・定理・命題・補題・系を完全理解しよう）。

補題の主張

補題

実数列 {an} \{a_n\} が条件収束するとする。
このとき，

an+=max⁡{0,an}an−=max⁡{0,−an} \begin{gathered} a_n^{+} = \max\{0, a_n\} \\ a_n^{-} = \max\{0, -a_n\} \\ \end{gathered}

として，{an} \{a_n\} を正の部分と負の部分に分けると，

∑n=1∞an+=∑n=1∞an−=∞ \sum_{n=1}^\infty a_n^{+} = \sum_{n=1}^\infty a_n^{-} =\infty

が成立する。

教科書では自明といって証明を省略されることもあるかもしれませんが，きちんと証明しておきましょう。

補題の証明

補題の証明

Pn={1≤k≤n∣ak≥0}Qn={1≤k≤n∣ak<0}P={1≤k∣ak≥0}Q={1≤k∣ak<0} \begin{gathered} P_n = \{ 1 \le k \le n \mid a_k \ge 0\} \\ Q_n = \{ 1 \le k \le n \mid a_k < 0\} \\ P = \{ 1 \le k \mid a_k \ge 0\} \\ Q = \{ 1 \le k \mid a_k < 0\} \end{gathered}

と定める。示すべきことは

∑k∈Pak=−∑k∈Qak=∞ \sum_{k \in P} a_k = - \sum_{k\in Q} a_k = \infty

である。ただし，∑k∈P \sum_{k \in P} のように書いたとき，この無限和は k k が小さい順に計算することにする。いま，

∑k=1n∣ak∣=∑k∈Pnak−∑k∈Qnak \sum_{k=1}^n |a_k| = \sum_{k \in P_n} a_k - \sum_{k \in Q_n} a_k

であり，n→∞ n\to\infty としたとき，左辺は ∞ \infty となるから，

∑k∈Pak=∞ or −∑k∈Qak=∞ \sum_{k \in P} a_k =\infty \text { or } - \sum_{k \in Q} a_k =\infty

である。加えて，

∑k=1nak=∑k∈Pnak+∑k∈Qnak \sum_{k=1}^n a_k = \sum_{k \in P_n} a_k + \sum_{k \in Q_n} a_k

であり，n→∞ n\to\infty としたとき左辺が収束することから，結局

∑k∈Pak=∞ and −∑k∈Qak=∞ \sum_{k \in P} a_k =\infty \text { and } - \sum_{k \in Q} a_k =\infty

でなければならない。

証明終

リーマンの再配列定理の証明

準備が整いましたので，定理の証明をしましょう。

-∞ < V < ∞ のとき

定理の証明；−∞<V<∞ -\infty < V < \infty のとき

P={1≤k∣ak≥0}Q={1≤k∣ak<0} \begin{gathered} P = \{ 1 \le k \mid a_k \ge 0\} \\ Q = \{ 1 \le k \mid a_k < 0\} \end{gathered}

とし，P P に属する正の整数を小さい順に p1<p2<p3<⋯ p_1 < p_2 < p_3 < \cdots ，Q Q に属する正の整数を小さい順に q1<q2<q3<⋯ q_1 < q_2 < q_3 < \cdots とかくことにする。

このとき補題より，

∑kapk=−∑kaqk=∞(1) \sum_k a_{p_k} = - \sum_k a_{q_k} = \infty\tag{1}

である。

全単射 φ ⁣:Z≥1→Z≥1 \varphi\colon \mathbb{Z}_{\ge 1} \to \mathbb{Z}_{\ge 1} を以下のように順々に定める：

∑k=1n−1aφ(k)≤V \sum_{k=1}^{n-1} a_{\varphi(k)} \le V のとき，

φ(n)=min⁡P∖{φ(k)∣1≤k≤n−1} \varphi(n) = \min P \setminus \{\varphi(k)\mid 1\le k \le n-1\}

∑k=1n−1aφ(k)>V \sum_{k=1}^{n-1} a_{\varphi(k)} > V のとき，

φ(n)=min⁡Q∖{φ(k)∣1≤k≤n−1} \varphi(n) = \min Q \setminus \{\varphi(k)\mid 1\le k \le n-1\}

ただし，∑k=10=0 \sum_{k=1}^0 = 0 と解釈して φ(1) \varphi(1) を定める。

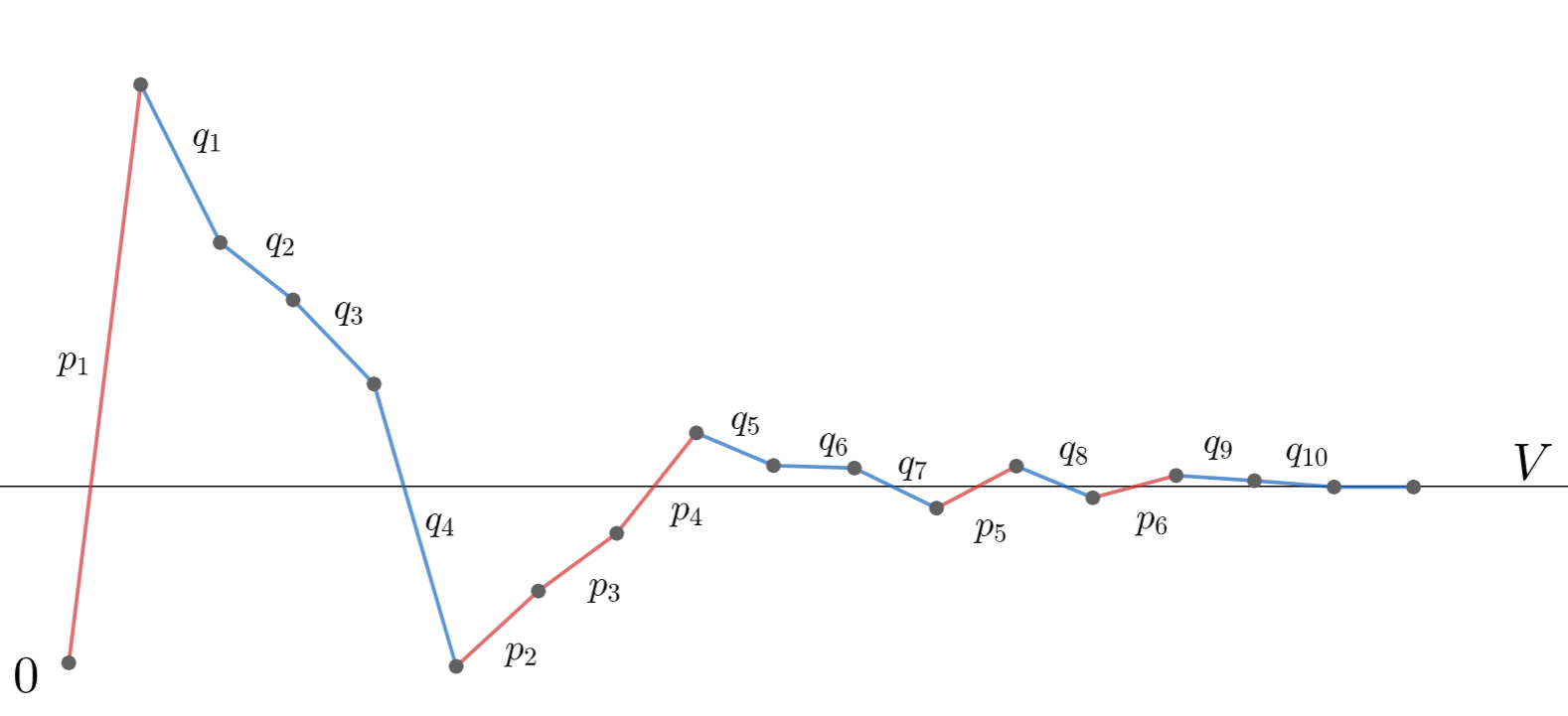
イメージ図を描くと以下のようになる。

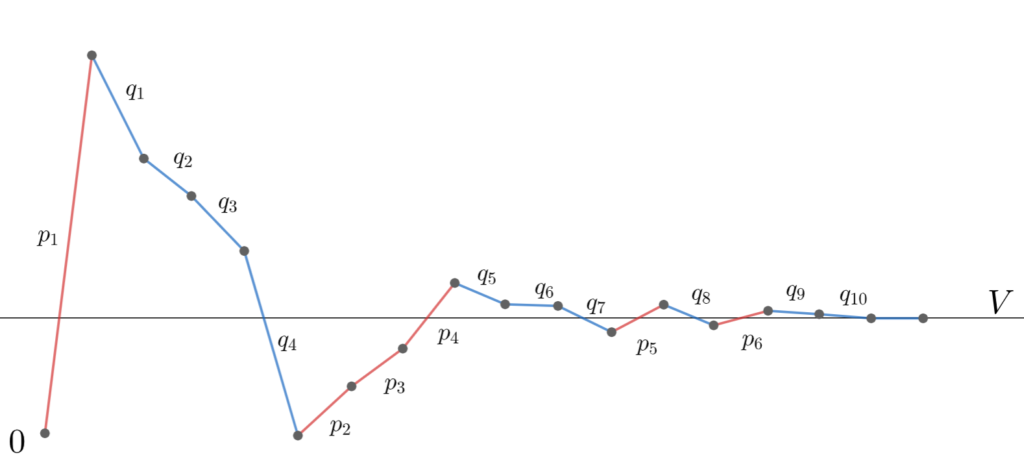
条件収束の項の並び替えのイメージ
条件収束の項の並び替えのイメージ(縦軸はΣの値を表す)

証明すべきは以下の2つである。
1. φ \varphi が確かに全単射であること
2. ∑n=1∞aφ(n)=V \sum_{n=1}^\infty a_{\varphi(n)} = V となること

順番に示そう。

1. φ \varphi が確かに全単射であること

定義の式から，φ(n) \varphi(n) は φ(1),φ(2),…,φ(n−1) \varphi(1), \varphi(2), \ldots ,\varphi(n-1) 以外から定めているため，単射である。

全射でないと仮定しよう。すなわち，ある m≥1 m \ge 1 が存在して，φ(k)=m \varphi(k) = m となる k k が存在しないとしよう。
m∈Q m \in Q とする。このとき，ある j j が存在して，m=qj m = q_j とかける。
φ \varphi の定め方から，任意の n≥1 n \ge 1 に対して

∑k=1napk+∑k=1j−1aqk≤V \sum_{k=1}^n a_{p_k} + \sum_{k=1}^{j-1} a_{q_k} \le V

となるが，これは (1) (1) 式に矛盾している。m∈P m \in P のときも同様である。

よって全単射となる。

2. ∑n=1∞aφ(n)=V \sum_{n=1}^\infty a_{\varphi(n)} = V となること

元の数列 ∑k=1∞an\sum_{k=1}^\infty a_n は収束していたから，特に an→0 a_n\to 0 であることに注意する。すなわち，任意の ε>0 \varepsilon > 0 に対し，ある N≥1 N \ge 1 が存在して，

n≥N  ⟹  ∣an∣≤ε n \ge N \implies | a_n | \le \varepsilon

である。ここで，M≥N M \ge N を

{φ(k)∣1≤k≤M}⊃{1,2,…,N} \{\varphi(k)\mid 1\le k \le M \} \supset \{1,2,\ldots, N\}

となるよう十分に大きくとる。このとき φ \varphi の定め方により，

n≥M  ⟹  ∣aφ(n)−V∣≤ε n \ge M \implies |a_{\varphi(n)} - V | \le \varepsilon

となる。よって，∑n=1∞aφ(n)=V \sum_{n=1}^\infty a_{\varphi(n)} = V である。

証明終

V = ± ∞ のとき

証明の本質は −∞<V<∞ -\infty < V < \infty と変わりませんから，図のみ示して演習問題としたいと思います。

略証；V=±∞ V = \pm \infty のとき

V=∞ V = \infty として一般性を失わない。

全単射 φ ⁣:Z≥1→Z≥1 \varphi\colon \mathbb{Z}_{\ge 1} \to \mathbb{Z}_{\ge 1} を和が図のようになるよう順々に定める。

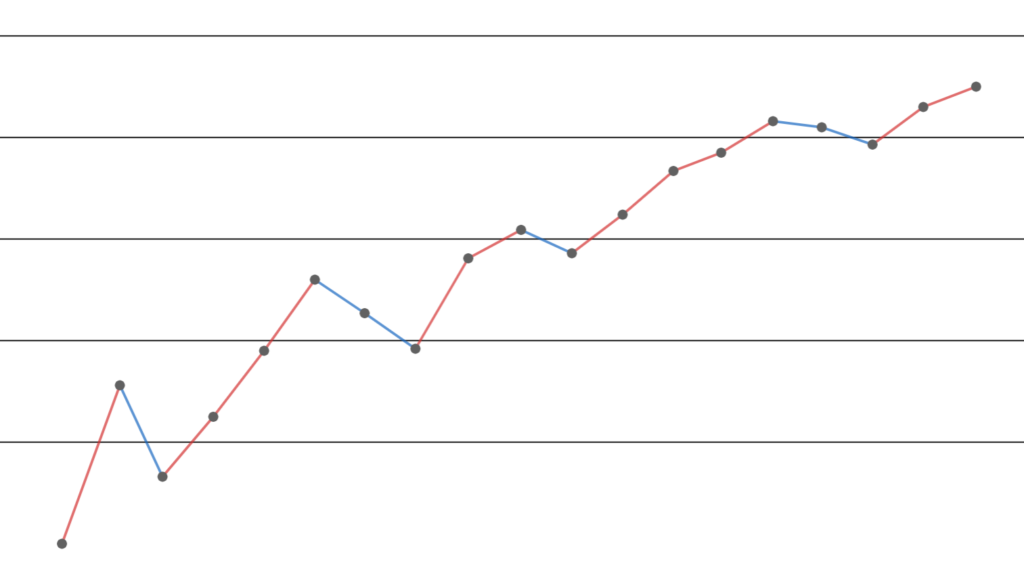
条件収束の項の並び替えのイメージ(∞に発散ver.)
条件収束の項の並び替えのイメージ(∞に発散ver.)

すなわち，「折り返すたびにボーダーを上げていく」ことにする。

あとの証明は −∞<V<∞ -\infty < V < \infty の場合とほぼ同様である。

略証終

絶対収束の場合は全く逆のことが成立する

条件収束ではなく，絶対収束するときは，以下の定理が知られています。

定理

数列 {an} \{a_n\} の和が絶対収束，すなわち ∑n=1∞∣an∣<∞ \sum_{n=1}^\infty |a_n| < \infty をみたすとする。
このとき，数列 {an} \{a_n\} と，正の整数の間の任意の全単射 φ ⁣:Z≥1→Z≥1 \varphi\colon \mathbb{Z}_{\ge 1} \to \mathbb{Z}_{\ge 1} によって項の順番を変えた数列 {aφ(n)} \{a_{\varphi(n)}\} の和は同じ値に収束する。すなわち，

∑n=1∞an=∑n=1∞aφ(n) \sum_{n=1}^\infty a_n = \sum_{n=1}^\infty a_{\varphi(n)}

となる。

項の順番を入れ替えても常に同じ値に収束すると言っているんですね。これは条件収束級数とは真逆だといえます。この証明については以下の記事を参照してください。

絶対収束級数は和の順序によらず同じ値に収束することの証明
有限和のときは，和の順序を入れ替えても値は同じになりますが，無限和のときは，一般にそうとは限りません。しかし，絶対収束級数においては，項の順番を任意に入れ替えても，同じ値に収束することが知られています。この定理を紹介し，証明しましょう。
mathlandscape.com

級数の収束・発散に関する他の話題