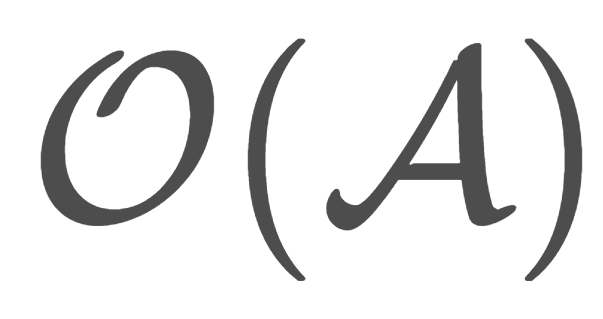PR

ハイネ–ボレルの被覆定理とその証明～有界閉区間のコンパクト性～

集合と位相

2025.01.012025.01.02

集合と位相

記事内に広告が含まれています。

ハイネ–ボレルの被覆（ひふく）定理とは，実数全体の集合に通常の位相を入れた位相空間において，有界閉区間はコンパクトであるという定理です。位相空間論の基本的な定理の一つです。

ハイネ–ボレルの被覆定理について，その内容の解説と，証明を行います。

目次

ハイネ–ボレルの被覆定理～有界閉区間のコンパクト性～
1. ハイネ–ボレルの被覆定理の主張
2. ハイネ–ボレルの被覆定理は有界閉区間じゃないとダメ
ハイネ–ボレルの被覆定理の証明
ハイネ–ボレルの被覆定理の一般化
関連する話題～点列コンパクト性～
関連する記事

ハイネ–ボレルの被覆定理～有界閉区間のコンパクト性～

まずは，ハイネ–ボレルの被覆定理の主張を述べて，その「お気持ち」を掘り下げたいと思います。

ハイネ–ボレルの被覆定理の主張

コンパクトという言葉の説明もしながら，定理の主張を述べましょう。

ハイネ–ボレルの被覆定理 (Heine–Borel theorem)

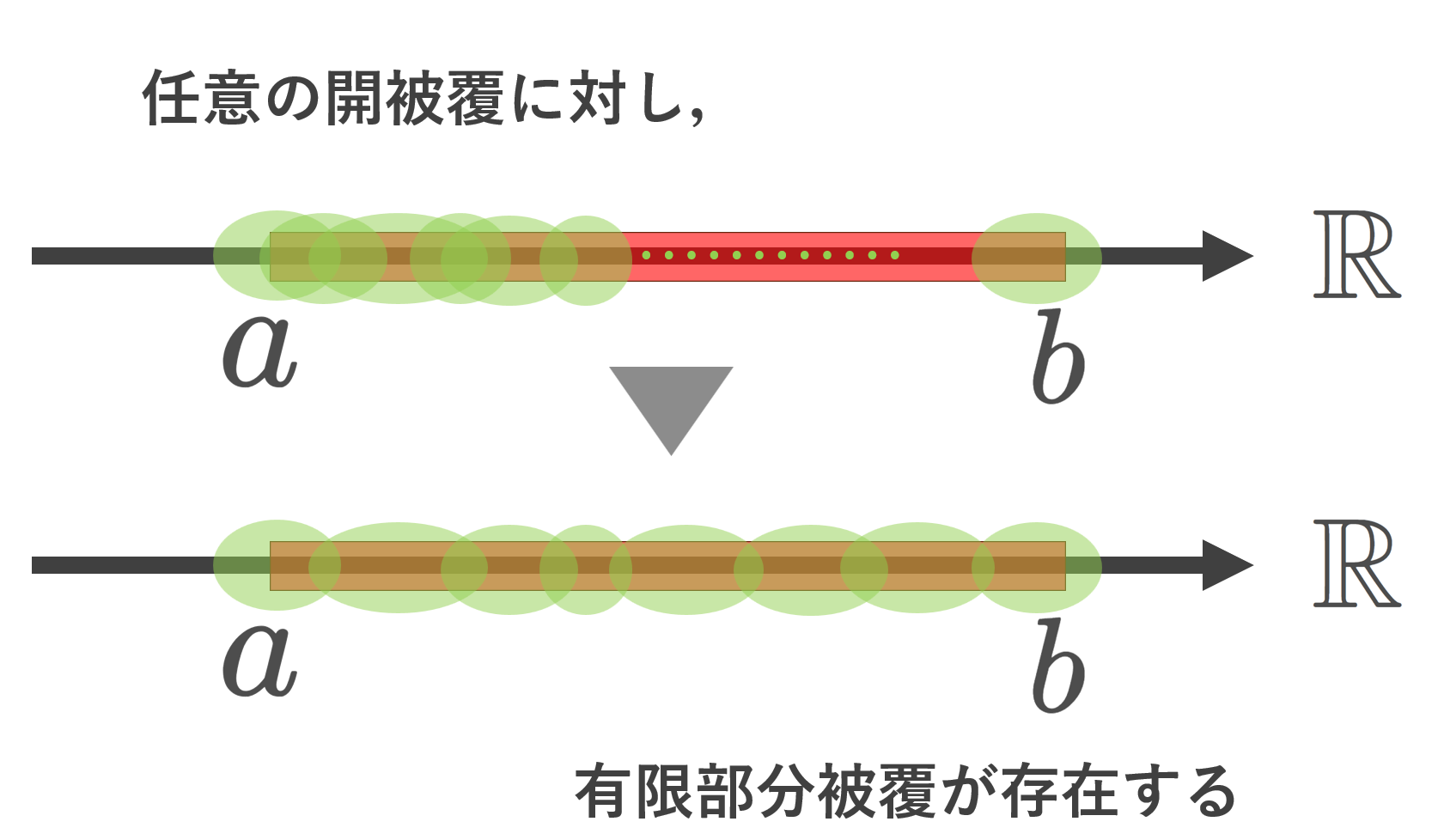
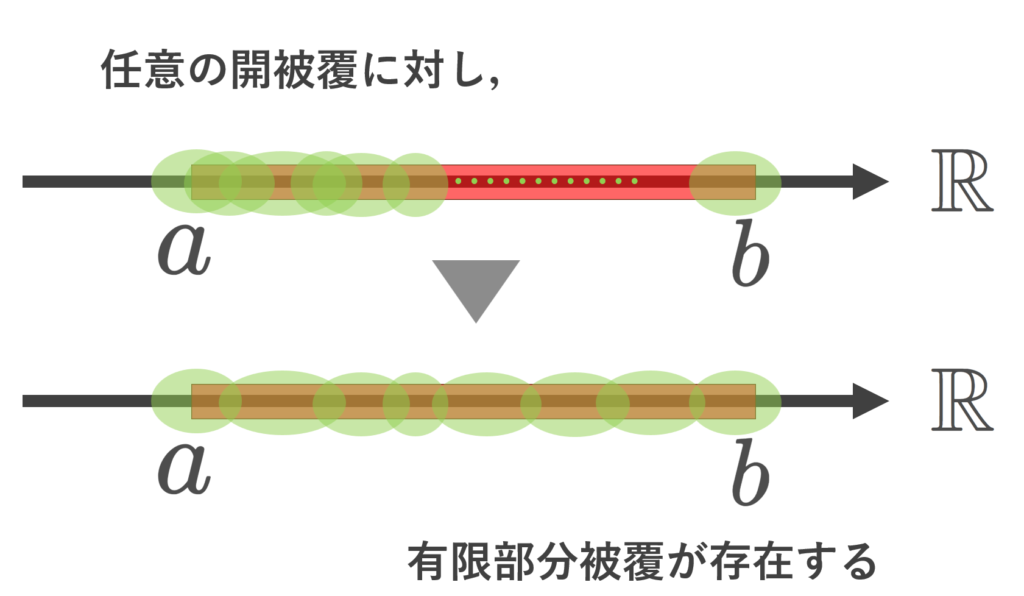
実数 $\R$ に通常の位相を入れた位相空間について，任意の有界閉区間 $[a,b]$ はコンパクトである。

すなわち， $[a,b]$ の任意の開被覆 $\{U_\alpha\}$ に対して，有限部分被覆 $\{ U_k\}_{k=1}^n\subset \{U_\alpha\}$ が存在する。

$\{U_\alpha\}$ が $[a,b]$ の開被覆 (open cover) であるとは，各 $U_\alpha$ が開集合でかつ

[a,b]\subset \bigcup_\alpha U_\alpha

をみたすことをいいます。 $\{ U_k\}_{k=1}^n$ が有限部分被覆であるとは， $\{U_\alpha\}$ の部分集合で，

[a,b]\subset \bigcup_{k=1}^n U_k

のように，有限個の開集合の和集合で覆えることを表します。

要するに，くだけて言うと， $[a,b]$ を開集合の和集合で覆うとき，どんな覆い方をしても，そこから有限個を選び出して，同じように $[a,b]$ を覆えるということです。「どんな覆い方をしてもそこから有限個を選んで」というのが重要で， $[a,b]\subset (a-1, b+1)$ とすれば1個の開集合で覆えるやんけ，ということではありません。

ハイネ–ボレルの被覆定理のイメージ図

ハイネ–ボレルの被覆定理は有界閉区間じゃないとダメ

$[a,b]$ はコンパクトですが， $(a,b)$ はコンパクトではありません。たとえば， $\{(a, b-1/n)\}_{n=1}^\infty$ は，

(a,b) = \bigcup_{n=1}^\infty \left(a, b-\frac{1}{n}\right)

とできるので，開被覆ですが，そこから有限個を選んできても，その和集合が $(a,b)$ を覆えるわけではないです。

また， $[a, \infty)$ もコンパクトではありません。たとえば， $\{(a-2+n, a+n)\}_{n=1}^\infty$ は開被覆ですが，そこから有限個を選んできても， $[a,\infty)$ は覆えません。

ハイネ–ボレルの被覆定理の証明

さて，ハイネ–ボレルの被覆定理，すなわち $[a,b]$ がコンパクトであることを証明していきましょう。 $(a,b)$ ではなぜ言えないのかまで考えながら進めていきましょう。

証明

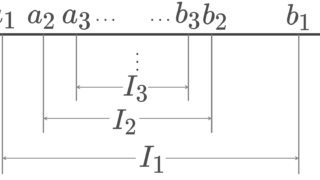
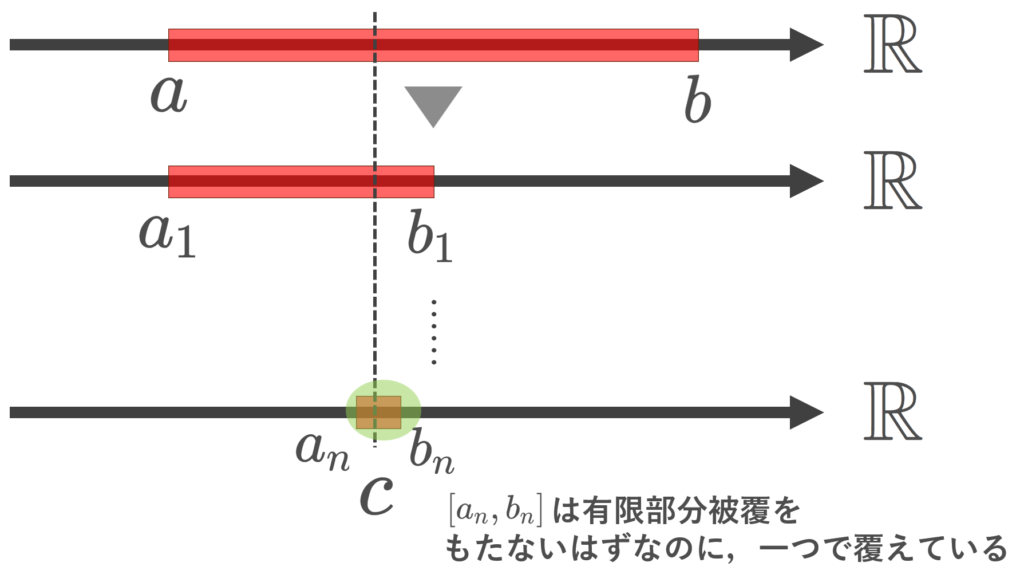
背理法で示す。 $[a,b]$ の開被覆 $\{U_\alpha\}$ が，有限部分被覆をもたないとする。このとき，この閉区間を2等分した

\left[a, \frac{a+b}{2}\right],\quad \left[\frac{a+b}{2}, b\right]

の少なくとも一方は $\{U_\alpha\}$ に属する有限個の開集合で被覆できない。その閉区間を $[a_1, b_1]$ とする。同様に2等分して，

\left[a_1, \frac{a_1+b_1}{2}\right],\quad \left[\frac{a_1+b_1}{2}, b_1\right]

のうち， $\{U_\alpha\}$ に属する有限個の開集合で被覆できない方を $[a_2, b_2]$ とする。以下帰納的に $[a_n, b_n]$ を取ると，閉区間の縮小列

[a,b]\supset [a_1, b_1]\supset [a_2, b_2]\supset [a_3, b_3]\supset\cdots

を得る。 $b_n-a_n = (b-a)/2^n \xrightarrow{n\to\infty} 0$ であるから，区間縮小法の原理により，

\bigcap_{n=1}^\infty [a_n, b_n]=\{c\}

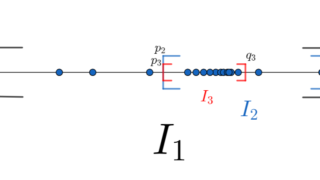
となる $a\le c\le b$ が存在する。 $c\in [a,b]\subset \bigcup_{\alpha} U_\alpha$ より， $c\in U_\alpha$ となるものが存在する。 $U_\alpha$ は開集合なので，ある $\varepsilon >0$ が存在して，

c\in (c-\varepsilon, c+\varepsilon ) \subset U_\alpha

とできる。 $b_n-a_n = (b-a)/2^n<\varepsilon$ となる $n\ge 1$ をとると，

c\in [a_n, b_n]\subset (c-\varepsilon, c+\varepsilon)\subset U_\alpha

となるが，これは， $[a_n, b_n]$ が有限部分被覆をもたないことに矛盾する(実際， $U_\alpha$ の一つで覆えている)。よって示された。

ハイネ–ボレルの被覆定理の証明のイメージ

証明終

途中で区間縮小法の原理を使いましたが，これは実数の連続性に関係しています。詳しくは以下の記事で解説しています。区間縮小法は開区間では成立しません。 $c\in (a,b)$ とは限りません。これが，上記の証明が $[a,b]$ の代わりに $(a,b)$ では成立しない理由です。

ハイネ–ボレルの被覆定理の一般化

ハイネ–ボレルの被覆定理より一般的な定理を述べておきましょう。

まず，ユークリッド空間 $\R^n$ においては以下が成立します。

定理（ $\R^n$ のコンパクト性）

$\R^n$ において， $A\subset \R^n$ が有界閉集合であることと，コンパクトであることは同値である。

より一般に距離空間においては，「有界閉集合」だけだと不十分です。次の定理が知られています。

定理（距離空間のコンパクト性）

距離空間 $(X,d)$ において， $A\subset X$ が全有界かつ完備であることと，コンパクトであることは同値である。

以上の2つの定理については，いずれ別の記事で解説しましょう。

関連する話題～点列コンパクト性～

$\R$ (より一般に距離空間)においては，ある集合がコンパクトであることと，点列コンパクトであることは同値です。ここで， $[a,b]$ が点列コンパクト (sequentially compact) であるとは，任意の点列 $\{x_n\}\subset [a,b]$ が収束する部分列を持つことを言います。

本記事では， $[a,b]$ がコンパクトであることの証明を行いましたが， $[a,b]$ が点列コンパクトであることの証明は，以下の記事で行っています。非常に似ている証明であることが分かると思います。

関連する記事