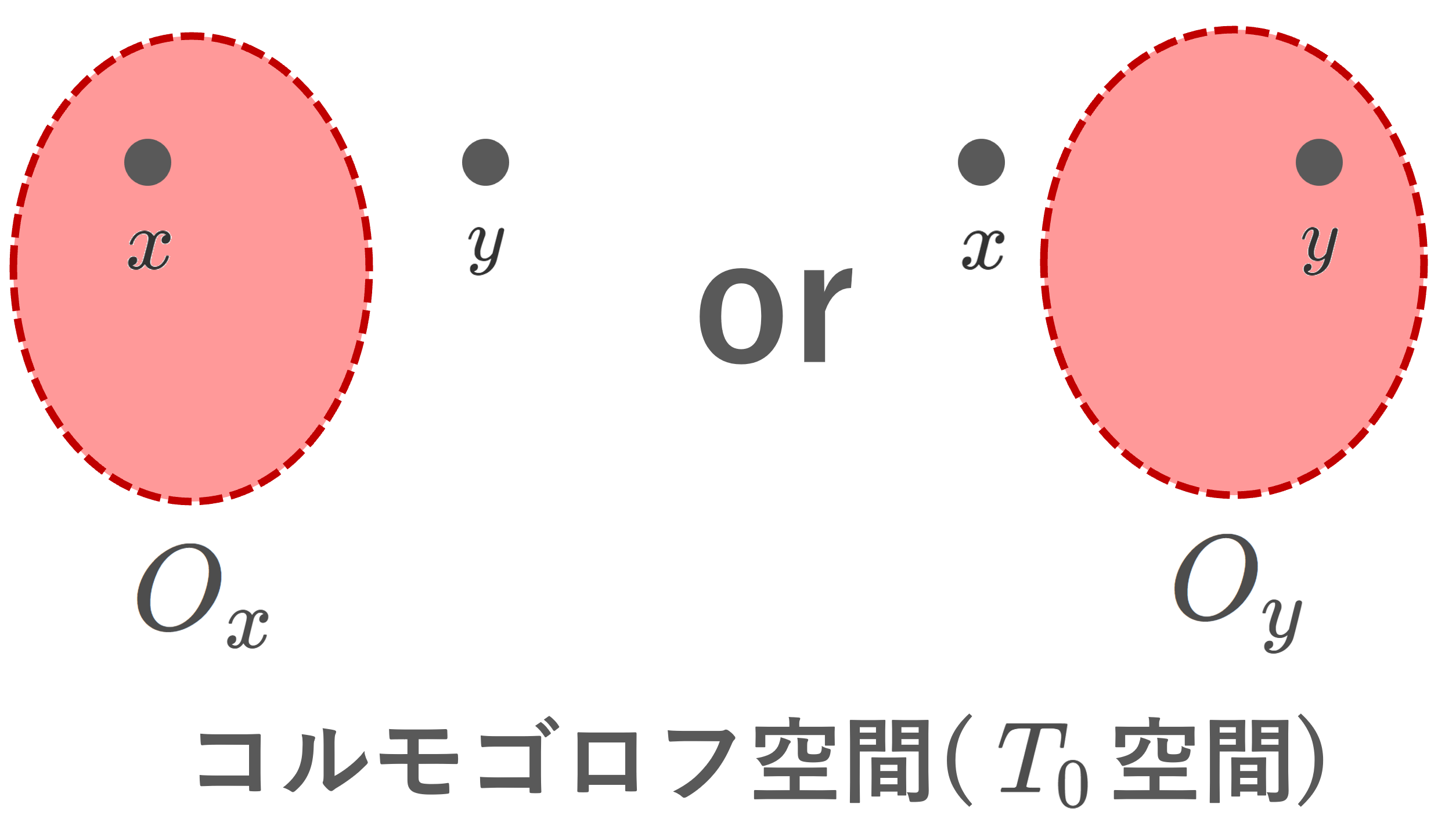
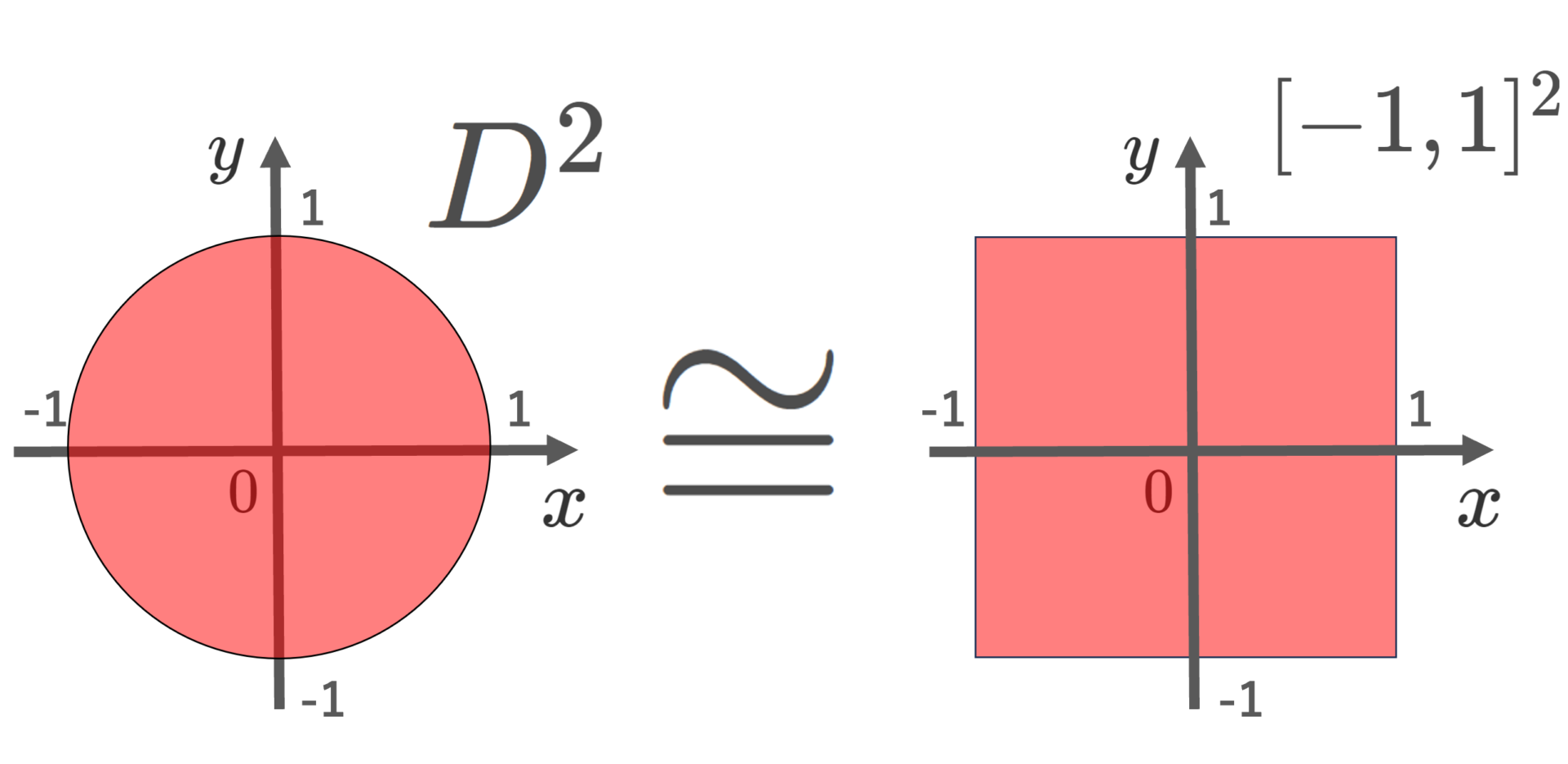同相写像とは，位相的性質を保つ写像のことで，同相写像が存在する2つの位相空間は，位相的性質が全く同じであり，そのような2つの位相空間は，同相(位相同型)であるといいます。これにより，位相空間を分類することが可能です。
同相写像と同相(位相同型)の定義・具体例・性質を紹介し，さらに，全単射かつ連続だけだと，同相写像とは言えないことも解説しましょう。
同相写像と同相(位相同型)
同相写像と同相(位相同型)の定義
定義（同相写像と同相(位相同型)）
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし， f\colon X\to Y とする。 f が
のすべて成り立つとき， f を同型写像 (homeomorphism) という。また，このときの位相空間 X と Y は同相または位相同型 (homeomorphic) であるといい，本サイトでは \large\color{red} (X,\mathcal{O}_X)\simeq (Y,\mathcal{O}_Y) または単に \large\color{red} X\simeq Y とかく。
定義から明らかに，f が全単射なら， f が同相写像 \iff f^{-1} が同相写像です。
同相(位相同型)なら，位相空間として同一視できる
f が連続であることの定義は， O_Y\in \mathcal{O}_Y \implies f^{-1} (O_Y)\in \mathcal{O}_X であり， f^{-1} が連続であることの定義は， O_X\in\mathcal{O}_X\implies f(O_X)\in\mathcal{O}_Y です(→位相空間における連続写像の定義と性質を詳しく)。
ここで， O_X = f^{-1}(O_Y) とおくと，f は全単射より， O_Y=f(O_X) です。よって， f が連続であることの定義は， f(O_X)\in \mathcal{O}_Y \implies O_X\in \mathcal{O}_X とかき直すことができます。これと， f^{-1} が連続であることを組み合わせると， f が同相写像なら
\Large \color{red} O_X\in\mathcal{O}_X\iff f(O_X)\in\mathcal{O}_Y
とかけます。同様に，O_Y\in\mathcal{O}_Y\iff f^{-1}(O_Y)\in\mathcal{O}_X も成り立ちます。同相写像は，開集合族同士も全単射の関係になっています。
これにより， (X,\mathcal{O}_X) と (Y, \mathcal{O}_Y) は全ての開集合が1対1に対応していることになります。したがって，同相(位相同型)なら，点 x\in X と点 f(x)\in Y，開集合 O_X\in\mathcal{O}_X と開集合 f(O_X)\in\mathcal{O}_Y を完全に同一視できることになります。開集合族を同一視できることから，閉集合族や，近傍系も同一視できることがわかります。
2つの空間が同相(位相同型)なら保たれる性質を位相的性質 (topological property) といいます。同相(位相同型)な2つの空間は，開集合族を同一視できるので，開集合族のみを用いて記述できる全ての性質が，位相的性質と言えます。たとえば，
- 分離公理（ハウスドルフ性・正規性・正則性など）
- コンパクト性（局所コンパクト性・点列コンパクト性なども含む）
- 連結性（弧状連結性・完全不連結性・単連結性・可縮性なども含む）
- 第一可算・第二可算性
- 可分性
- 距離化可能性
- ホモトピー群
- ホモロジー群
などは全て位相的性質です。一方で，
などは，位相的性質ではありません。たとえば，ユークリッド空間 \R^n において，ユークリッド距離とマンハッタン距離は距離空間としては別物ですが，入る位相は同じなので，位相空間としては同相(位相同型)です。具体的な距離は，同相(位相同型)でも保たれないことが説明できました。
同相(位相同型)な空間とそうでない例
2つの空間が同相(位相同型)であることを示すには，一つ同相写像を構成すればよいです。逆に，同相でないことを示すには，任意の写像が同相写像にならないことを示さなければならず，これを直接示すのは大変です。そこで，直前で述べたことを利用します。同相でないことを示すには，位相的性質が異なることを言えばよいです。
例1.
a<b に対し， (a,b)\simeq \R
たとえば， \displaystyle f(x)=\tan \frac{\left(x-\frac{a+b}{2}\right)\pi}{b-a} とすれば， f\colon (a,b)\to \R は同相写像です。
\R は完備ですが， (a,b) は完備ではありません。完備性は位相的性質ではありません。
例2.
D^1\simeq [-1,1]^2ただし，D^1=\{(x,y)\in\R^2\mid x^2+y^2\le 1\} を単位閉円板とする。
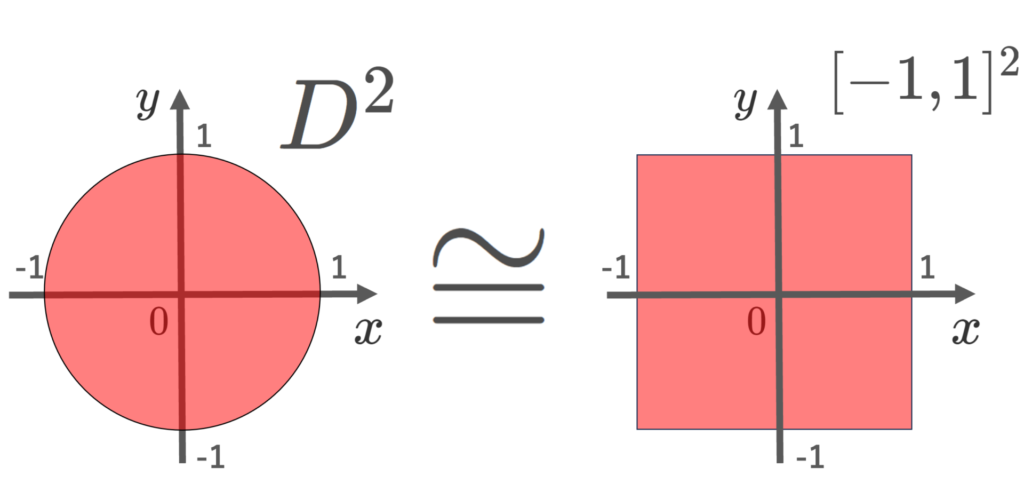
極座標が (r,\theta) である点を \left(1/\max\{|\cos\theta|, |\sin\theta|\}, \theta\right) にうつす写像は同相写像です。
位相空間を粘土だと思うと，同相(位相同型)な2つの位相空間は，粘土を伸び縮みさせて（切断・結合はしない），互いにもう一方に変形させることができる，と言われることがあります。このように図形を粘土だと思って分類し，性質を調べる数学の分野を位相幾何学 (topology) といいます。
例3.
a<b に対し， (a,b)\not\simeq [a,b]
(a,b) はコンパクトではありませんが， [a,b] はコンパクトです(→ハイネ–ボレルの被覆定理とその証明～有界閉区間のコンパクト性～)。位相的性質が違うので，同相(位相同型)ではありません。
例4.
[0,2\pi)\not\simeq S^1ただし，S^1=\{(x,y)\in\R^2\mid x^2+y^2=1\} を単位円とする。
証明には少しテクニックが必要です。 f\colon [0,2\pi)\to S^1 を同相写像とすると，後の定理2より，\pi\in [0,2\pi) と，対応する S^1 上の点 f(\pi) を除いた空間も同相になり， [0,2\pi)\setminus \{\pi\}\simeq S^1\setminus \{f(\pi)\} となるはずです。
しかし， [0,2\pi)\setminus\{\pi\} は連結でないのに対し，S^1\setminus \{f(p)\} は連結なので，これは矛盾しています。よって，[0,2\pi)\not\simeq S^1 が示せました。
「どんな」写像でも同相写像でないと言えなければなりませんから，例えば x\mapsto (\cos x, \sin x) が同相写像でないことを示すだけだと不十分です。
例5.
\R\simeq S^1\setminus\{(1,0)\}ただし，S^1=\{(x,y)\in\R^2\mid x^2+y^2=1\} を単位円とする。
右辺は S^1 から1点を除いた集合であれば，なんでも良いです。
例1.より， \R\simeq (0,2\pi) です。x\mapsto (\cos x, \sin x) により， (0,2\pi)\simeq S^1\setminus\{(1,0)\} が分かるので，後の定理4.により，\R\simeq S^1\setminus\{(1,0)\} を得ます。
例6.
H=\{(x,y)\in \R^2\mid xy=1\} とすると， H\simeq \R\setminus\{0\} である。
H は xy 平面上における双曲線 y=1/x です。 f(x,y)=x とすると， f\colon H\to \R\setminus\{0\} は同相写像です。実際， f^{-1}(x)=(x,1/x) も連続です。
例7.
正の整数 m\ne n に対し，\R^m\not\simeq \R^n
これを一般に示すのは，深い知識が必要です。一部の特別な場合は簡単に示せます。
m> 1 のとき， \R^m\not\simeq \R であることは，例3.の方針と同じです。f\colon \R\to \R^m を同相写像とすると，その制限により \R\setminus\{0\}\simeq \R^m\setminus\{f(0)\} となるはずですが，左辺は連結でなく，右辺は連結なので矛盾しています。よって示せました。
m>2 のとき， \R^m\not\simeq \R^2 であることを示しましょう。f\colon \R^2\to \R^m を同相写像とすると，その制限により \R^2\setminus\{0\}\simeq \R^m\setminus\{f(0)\} となるはずですが，左辺は単連結でなく，右辺は単連結なので，矛盾しています。
一般の m\ne n について，同相でないことの概要を記しておきましょう。もし，\R^m\simeq \R^n ならば，1点コンパクト化して，S^m\simeq S^n も成り立つはずです。ただし， S^m, S^n はそれぞれ m,n 次元超球面です。しかし，一般にホモロジー群について，
H_i(S^j) = \begin{cases} \mathbb{Z} & i=0,j,\\ 0 & i\ne 0,j \end{cases}
ですから，S^m と S^n のホモロジー群は一致せず，これは矛盾です。よって，\R^m\not\simeq \R^n が示せました。
同相写像と同相(位相同型)の性質
同相写像とは，連続全単射で，かつ「 f^{-1} も連続」と定義しましたが，「 f^{-1} も連続」の部分は， f の別の条件で言い換え可能です。
定理1（同相写像と開写像・閉写像）
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし， f\colon X\to Y を全単射かつ連続とする。このとき，以下の3つは同値である。
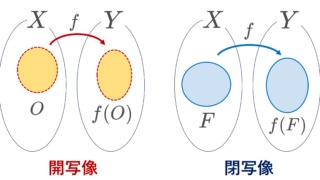
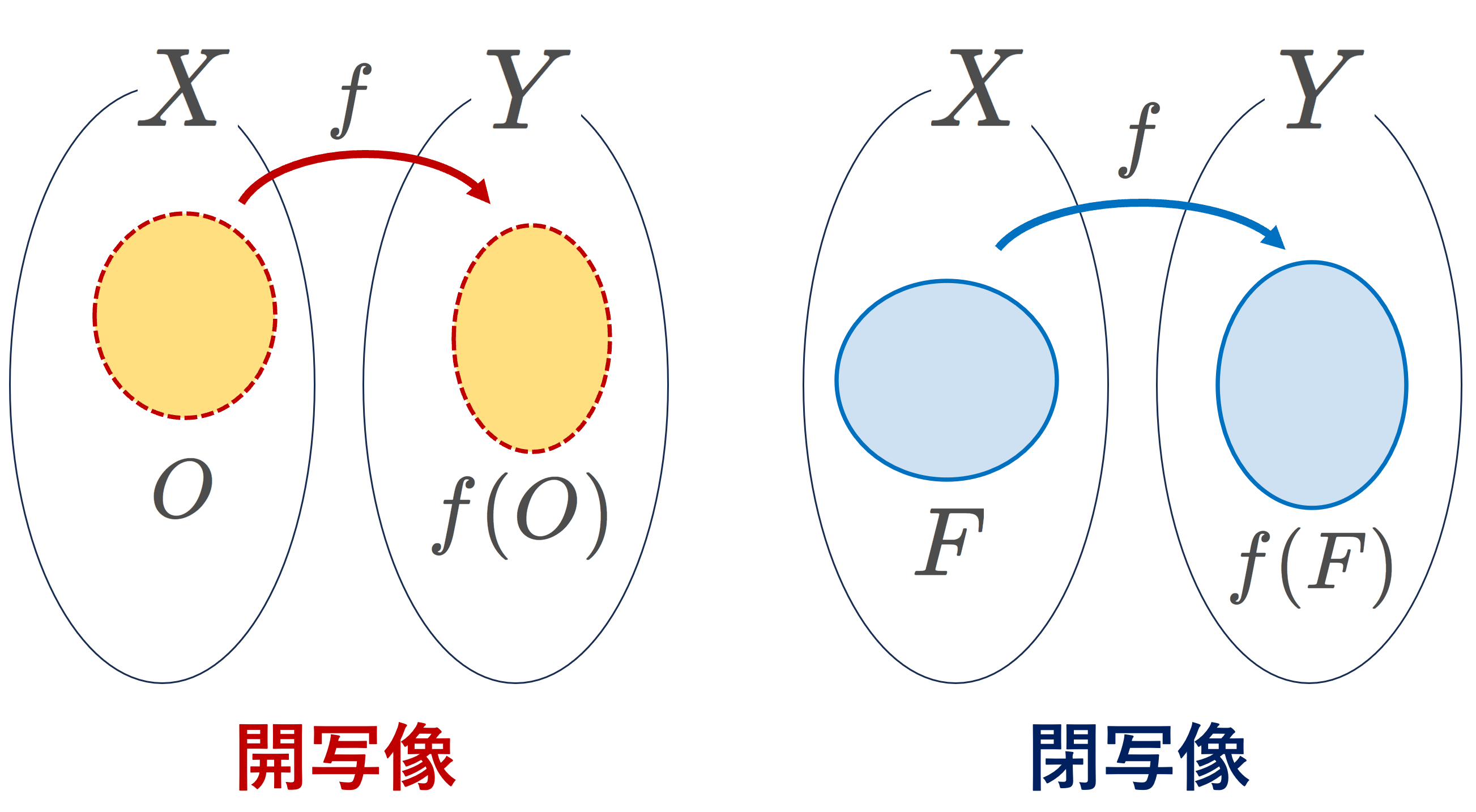
開写像とは，O\in\mathcal{O}_X\implies f(O)\in\mathcal{O}_Y すなわち，開集合を開集合にうつす写像のことで，閉写像とは，閉集合を閉集合にうつす写像のことです(→開写像・閉写像の定義・具体例10個・性質4つ)。
これの証明は，以下の記事で行っています。
定理2（同相写像の制限）
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし， f\colon X\to Y を同相写像とする。
A\subset X に対し， f の A 上への制限 f|_A\colon A\to f(A) を考えると， f|_A も同相写像である。ただし，位相空間 A\subset X,\, f(A)\subset Y は，それぞれ X, Y の部分空間と考える。
証明
f|_A\colon A\to f(A) が全単射であることは良い。また，連続写像の定義域や終域を制限した写像が連続になることは，位相空間における連続写像の定義と性質を詳しくの中で解説している。
また， (f|_A)^{-1}\colon f(A)\to A は， (f|_A)^{-1}=(f^{-1})|_{f(A)} と見れるので，f^{-1} が連続であることと， (f|_A)^{-1} はその制限と見ることで同様に連続だとわかる。
証明終
次は，同相な位相空間が同一視できることから明らかです。
定理3（同相な空間同士の開集合・閉集合）
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし， f\colon X\to Y を同相写像とする。このとき，A\subset X に対し，
- f(\operatorname{Int}(A))=\operatorname{Int}(f(A))
- f(\overline{A})=\overline{f(A)}
左辺と右辺で， X,Y どちらの空間で内部(開核)・閉包を考えているのかが異なりますので，注意が必要です。次も簡単に示せます。
定理4（同相(位相同型)の関係は同値関係）
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y),(Z,\mathcal{O}_Z) を位相空間とし， f\colon X\to Y,\, g\colon Y\to Z を同相写像とする。このとき，
- 恒等写像 \mathrm{id}\colon X\to X は同相写像である
- f^{-1}\colon Y\to X も同相写像である
- g\circ f\colon X\to Z も同相写像である
以上から，
- X\simeq X
- X\simeq Y\implies Y\simeq X
- X\simeq Y, Y\simeq Z\implies X\simeq Z
が成り立つため，同相(位相同型)の関係は同値関係である。
同値関係については，以下の記事を見てください。
全単射かつ連続だけだと同相写像とは言えない
f\colon X\to Y が同相写像であることの定義は，
の3つが必要でした。中には，3つめの条件はなくても自動的に言えるのではと思った人もいるかもしれませんが，そうではありません。ここでは，全単射かつ連続が成り立ちますが，同相写像でない，すなわち逆写像が連続でない例を挙げましょう。
全単射連続写像だが逆写像が連続でない例
[0, \pi)\subset [0,2\pi) は \R の通常の位相の相対位相によって開集合ですが， f([0,\pi)) は開集合ではありません。
逆写像が連続でない例2.
X を空でない集合とし，\mathcal{O}_1,\mathcal{O}_2 をその上の位相とする。 \mathcal{O}_1\supsetneq \mathcal{O}_2 のとき，恒等写像 \mathrm{id}\colon (X,\mathcal{O}_1)\to (X,\mathcal{O}_2) は全単射かつ連続だが，逆写像は連続でない。
もっと初等的な例も挙げておきましょう。
逆写像が連続でない例3.
f\colon (-\infty, 0)\cup [1,\infty)\to \R を，f(x)=\begin{cases}x &x<0, \\ x-1 & x\ge 1 \end{cases} と定めると，f は全単射・単調増加・連続だが，逆写像は連続でない
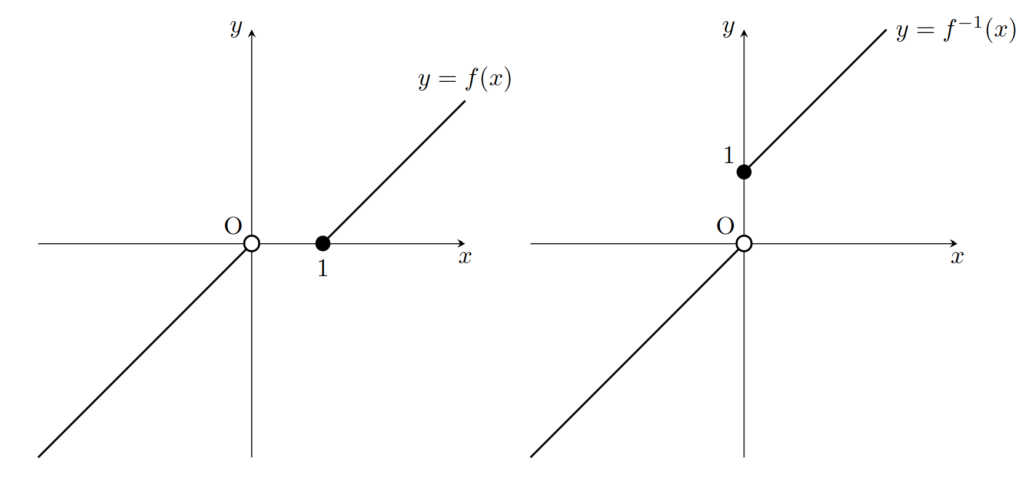
まず， f が連続であることに注意してください。初等的な連続の定義は，全ての定義域内の a に対し， \lim_{x\to a} f(x)=a が成り立つことでした。これはみたしていますので， f は連続です。
f^{-1}(x)=\begin{cases}x & x<0,\\ x+1 & x\ge 0 \end{cases} ですから， f^{-1}\colon \R\to (-\infty, 0)\cup [1,\infty) は連続ではありません。たとえば， [1,2) は (-\infty, 0)\cup [1,\infty) 上開集合ですが， f^{-1} における [1,2) の逆像 f([1,2))=[0,1) は \R 上開集合ではありません。
コンパクト空間からハウスドルフ空間の全単射連続写像は同相写像
さて上の議論により，一般に全単射かつ連続だけだと，逆写像が連続とは言えず，同相写像とは言えないことを確認しました。しかし，条件を付ければ，同相写像にすることができます。述べましょう。
定理5（コンパクトハウスドルフ空間）
(X,\mathcal{O}_X) をコンパクト空間， (Y,\mathcal{O}_Y) をハウスドルフ空間とする。 f\colon X\to Y が全単射で連続であるとき， f は同相写像である。
端的な証明を紹介しましょう。
証明
定理1.より， f が閉写像であることを示せばよい。
F\subset X を \mathcal{O}_X-閉集合とする。コンパクト空間の閉部分集合はコンパクトなので， F はコンパクトである。
コンパクト集合の像はコンパクトなので， f(F) はコンパクトである。
ハウスドルフ空間におけるコンパクト集合は閉集合なので， f(F) は \mathcal{O}_Y 閉集合である。よって題意は示された。
証明終
