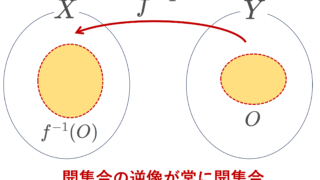
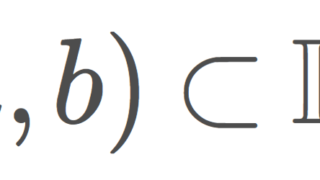「位相空間の間の写像が連続写像になる」という話を転換して,「間の写像が連続になるよう位相空間を定める」という議論を行うのが,誘導位相の考え方です。定義域側に定まる位相を始位相,終域側に定まる位相を終位相といいます。
本記事では,始位相・終位相の定義と具体例,普遍性と呼ばれる性質を紹介します。
始位相・終位相の定義

まずは始位相の定義・終位相の定義を一気に述べましょう。
始位相の定義
定義(始位相)
X を空でない集合とし, \{(Y_\lambda, \mathcal{O}_\lambda)\}_{\lambda\in \Lambda} を位相空間の族とする。さらに \{ f_\lambda\colon X\to Y_\lambda\}_{\lambda\in\Lambda} を写像の族とする。
全ての \lambda\in \Lambda について, f_\lambda \colon X\to Y_\lambda が連続写像となる X の最小の位相(最弱の位相) \mathcal{O}_Xを, \{f_\lambda\}_{\lambda\in\Lambda} によって誘導される始位相 (initial topology) という。 \mathcal{O}_X は
\{ {f_\lambda}^{-1}(O_\lambda)\mid \lambda\in\Lambda,\, O_\lambda \in\mathcal{O}_\lambda\}
を準開基とする位相である。
言い換えると,
\left\{ \bigcap_{k=1}^n {f_{\lambda_k}}^{-1}(O_{\lambda_k})\middle| \begin{aligned} &n\ge 1, \, \lambda_k \in\Lambda_k, \\ &O_{\lambda_k} \in\mathcal{O}_{\lambda_k} , k= 1,\ldots, n \end{aligned}\right\}
を開基とする位相です。
また, \Lambda が1点集合のとき,すなわち, (Y, \mathcal{O}_Y) を位相空間, f\colon X\to Y を写像としたとき, f によって誘導される始位相 \mathcal{O}_X は
\mathcal{O}_X = \{ f^{-1}(O)\mid O\in\mathcal{O}_Y\}
です。定義に従えば右辺を準開基とする位相ですが,右辺自体が位相空間の定義をみたしているので,右辺が \mathcal{O}_X そのものとなっています。
X に離散位相を入れると,全ての f_\lambda は明らかに連続になります。連続性は,定義域の位相が大きい(強い)ほど成り立ちやすくなりますから(→位相空間における連続写像の定義と性質を詳しく), X に入る最小の位相(最弱の位相)を求めていることに意味があります。
比較のため,すぐ終位相の定義を述べましょう。
終位相の定義
定義(終位相)
\{(X_\lambda,\mathcal{O}_\lambda)\}_{\lambda\in\Lambda} を位相空間の族とし, Y を空でない集合とする。さらに \{f_\lambda \colon X_\lambda\to Y\}_{\lambda\in\Lambda} を写像の族とする。
全ての \lambda\in \Lambda について, f_\lambda \colon X_\lambda \to Y が連続写像となる X の最大の位相(最強の位相) \mathcal{O}_Yを, \{f_\lambda\}_{\lambda\in\Lambda} によって誘導される終位相 (final topology) という。 \mathcal{O}_Y は
\mathcal{O}_Y=\{ O\subset Y\mid \forall \lambda\in\Lambda,\, {f_\lambda}^{-1}(O)\in\mathcal{O}_\lambda\}
と表せる。
右辺が位相空間であることは,写像の像・逆像と集合との演算証明からわかります。
Y を密着位相とすると,全ての f_\lambda は明らかに連続になります。連続性は,終域の位相が小さい(弱い)ほど成り立ちやすくなりますから(→位相空間における連続写像の定義と性質を詳しく),今度は Y に入る最大の位相(最強の位相)を求めていることに意味があります。
始位相・終位相の具体例
例1(恒等写像).
(X,\mathcal{O}) を位相空間とする。恒等写像 f\colon X\to (X,\mathcal{O}) によって誘導される始位相は \mathcal{O} であり,恒等写像 f\colon (X,\mathcal{O})\to X によって誘導される終位相も \mathcal{O} である。
例2(相対位相).
(X,\mathcal{O}) を位相空間とし, A\subset X とする。このとき,包含写像 \iota\colon A\to X によって誘導される, A 上の始位相 \mathcal{O}_A を相対位相 (relative topology) という(→相対位相と部分位相空間の定義・具体例5つ・性質5つ)。
となります。
例3(直積位相).
\{ (X_\lambda,\mathcal{O}_\lambda)\}_{\lambda\in\Lambda} を位相空間の族とする。このとき,直積からの射影
p_\lambda \colon \prod_{\lambda\in\Lambda} X_\lambda \to X_\lambda, \quad \lambda\in \Lambda
の族 \{p_\lambda\} によって誘導される,直積集合 \prod_{\lambda\in\Lambda} X_\lambda に入る始位相を直積位相 (積位相,product topology) という。
直積位相については,以下で解説しています。
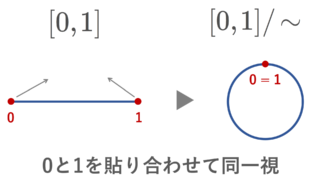
例4(商位相).
(X,\mathcal{O}) を位相空間とし, X 上の同値関係 \sim による商集合 X/\sim を考える。このとき,自然な射影
p\colon X\to X/\sim
によって誘導される, X/\sim に入る終位相を商位相 (quotient topology) という。
商位相については,以下で解説しています。
例5(直和位相).
\{ (X_\lambda,\mathcal{O}_\lambda)\}_{\lambda\in\Lambda} を位相空間の族とする。このとき,
\coprod_{\lambda\in\Lambda} X_\lambda = \{ (x_\lambda, \lambda) \mid x_\lambda\in X_\lambda, \, \lambda\in \Lambda\}
を直和とすると,自然な包含写像
が定まる。この族 \{\varphi_\lambda\} によって誘導される, \coprod_{\lambda\in\Lambda} X_\lambda 上の終位相を直和位相 (disjoint union topology) という。
もう少し具体的な例も挙げましょう。
例6(下限位相).
通常の意味で右連続である関数 f \colon \R\to \R 全体の集合を \mathcal{F} とする。 \mathcal{F} によって \R に誘導される始位相は,
\mathcal{O}_l=\{ [a,b)\mid a<b,\, a,b\in\R\}
を開基とする位相である。この位相を下限位相 (lower limit topology) といい, (\R,\mathcal{O}_l) をゾルゲンフライ直線 (Sorgenfrey line) という。ただし,終域には通常の位相が入っているものとする。
下限位相は, (a,b) も開集合に持ち, \R の通常の位相より真に大きい(細かい)位相です。以下で解説しています。
始位相・終位相の普遍性
普遍性と呼ばれる概念を紹介しておきましょう。圏論からくる概念です。
始位相の普遍性
定理1(始位相の普遍性)
X を空でない集合とし, \{(Y_\lambda, \mathcal{O}_\lambda)\}_{\lambda\in \Lambda} を位相空間の族とし,さらに \{ f_\lambda\colon X\to Y_\lambda\}_{\lambda\in\Lambda} を写像の族とする。
\{f_\lambda\} によって誘導される始位相を \mathcal{O}_X とする。さらに (W,\mathcal{O}_W) を位相空間とし, g\colon W\to X とする。このとき,次の2つは同値
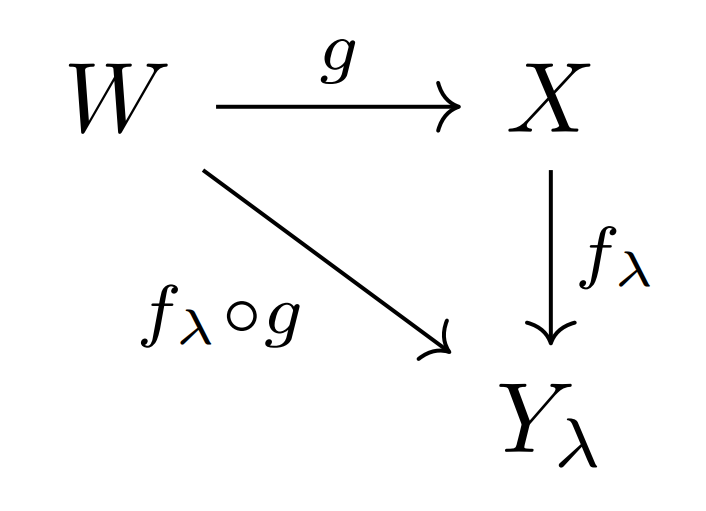
証明
1.\implies 2.は連続写像の合成は連続なので明らか(→位相空間における連続写像の定義と性質を詳しく)。
2. \implies 1.について
O_\lambda \in \mathcal{O}_\lambda とすると, {f_\lambda}^{-1} (O_\lambda)\in \mathcal{O}_X である。また, (f_\lambda\circ g)^{-1}=g^{-1}\circ {f_\lambda}^{-1} であり, f_\lambda\circ g は連続であるから, g^{-1}({f_\lambda}^{-1} (O_\lambda))\in\mathcal{O}_W である。
\mathcal{O}_X は \{ {f_\lambda}^{-1}(O_\lambda)\mid \lambda\in\Lambda,\, O_\lambda \in\mathcal{O}_\lambda\} を準開基とするため,\mathcal{O}_X–準開基の g による逆像が常に \mathcal{O}_W-開集合になると言えたので, g は連続である。
証明終
終位相の普遍性
定理2(終位相の普遍性)
\{(X_\lambda,\mathcal{O}_\lambda)\}_{\lambda\in\Lambda} を位相空間の族とし, Y を空でない集合とする。さらに \{f_\lambda \colon X_\lambda\to Y\}_{\lambda\in\Lambda} を写像の族とする。
\{f_\lambda\} によって誘導される終位相を \mathcal{O}_Y とする。さらに (Z,\mathcal{O}_Z) を位相空間とし, g\colon Y\to Z とする。このとき,次の2つは同値
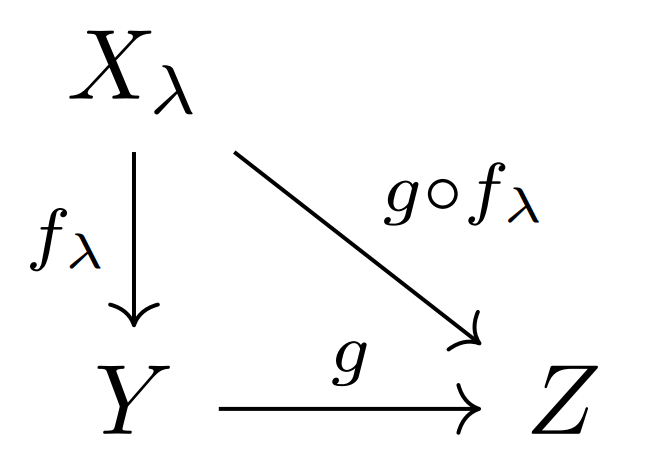
証明
1.\implies 2.は連続写像の合成は連続なので明らか(→位相空間における連続写像の定義と性質を詳しく)。
2. \implies 1.について
(g\circ f_\lambda)^{-1}= {f_{\lambda}}^{-1}\circ g^{-1} に注意する。 O\in\mathcal{O}_Z とすると, g\circ f_\lambda は連続より, {f_{\lambda}}^{-1}(g^{-1}(O))\in\mathcal{O}_\lambda である。
終位相の定義より, g^{-1}(O)\in\mathcal{O}_Y となるから, g は連続である。
証明終