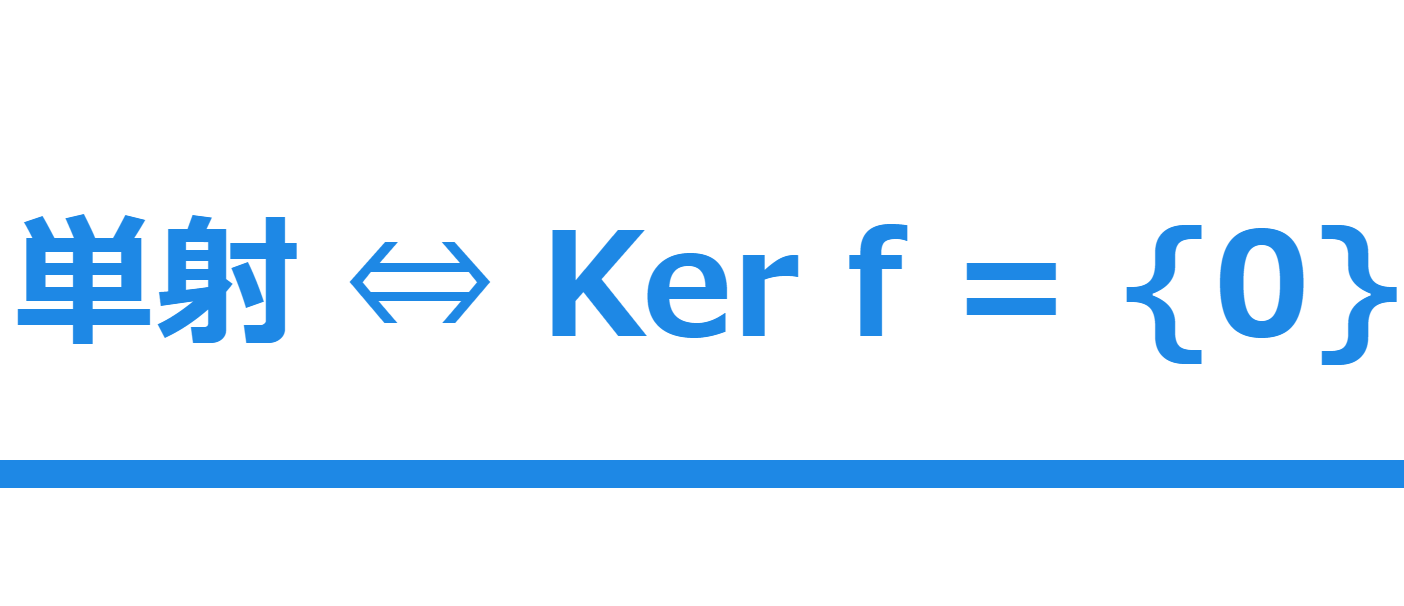今回のテーマは,いつ線形写像が全射・単射になるか,特にいつ単射になるかについては非常に大事なので,これについて証明します。
線形写像が全射・単射になる必要十分条件
定理(線形写像の全射・単射性)
V, W をベクトル空間, f\colon V\to W を線形写像とする。
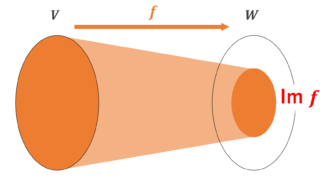
このとき,これが全射になる必要十分条件は
となることで,単射になる必要十分条件は
となることである。
\operatorname{Im}, \operatorname{Ker} の定義は上のカッコの中に書いた通りですが,これについてもっと詳しく知りたい場合は以下を参照してください。
全射の方は,定義から明らかというか定義そのままなので,これ以上述べません。
単に,「単射と \operatorname{Ker} のような関係が全射と \operatorname{Im} にもある」ということを比較したくて書きました。
単射 ⇔ Ker f = {0} の証明
それでは,単射の方の証明をしましょう。線形性が非常に重要な意味を持ちます。
証明
単射 \implies \operatorname{Ker} f = \{\boldsymbol{0}\} について
\boldsymbol{a} \in \operatorname{ker} f すなわち f(\boldsymbol{a}) = \boldsymbol{0} とする。線形写像なので f(\boldsymbol{0}) = \boldsymbol{0} であり(→線形写像の定義・性質と具体例8つ),これと単射性から, f(\boldsymbol{a}) = \boldsymbol{0} \implies \boldsymbol{a} = \boldsymbol{0} が従う。よって \operatorname{Ker} f = \{\boldsymbol{0}\}.
\operatorname{Ker} f = \{\boldsymbol{0}\} \implies 単射について
f(\boldsymbol{a}) = f(\boldsymbol{b}) としよう。このとき線形性より,
f(\boldsymbol{a} - \boldsymbol{b}) = f(\boldsymbol{a}) - f(\boldsymbol{b}) = \boldsymbol{0}
となるため, \boldsymbol{a} - \boldsymbol{b} \in \operatorname{Ker} f が分かる。 \operatorname{Ker} f = \{\boldsymbol{0}\} であったから, \boldsymbol{a} = \boldsymbol{b} であり,これは単射を意味する。
証明終
丁寧に証明しましたが,前半は明らかで,後半が大切です。線形写像が単射であるかを確認したければ, \operatorname{Ker} f を見るだけでよいということがポイントです。
より発展的な定理
本定理に関連して,以下のことが成り立ちます。
定理(線形写像の次元等式)
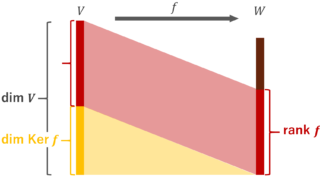
V, W をベクトル空間, f\colon V\to W を線形写像とする。このとき,
\color{red} \dim V = \operatorname{rank} f + \dim \operatorname{Ker} f
となる。
ここで \operatorname{rank} とは,日本語では階数と呼ばれ, \color{red} \operatorname{rank} f = \dim \operatorname{Im} f と定義されます。
これの証明は,以下を参照してください。