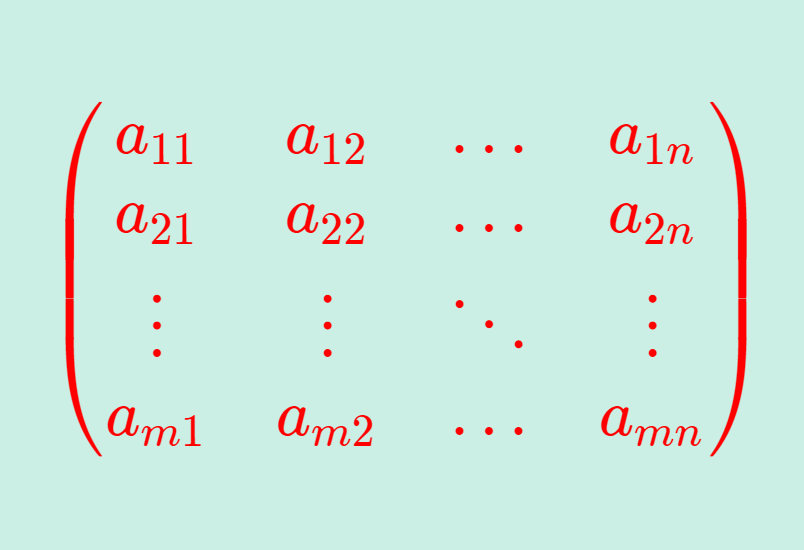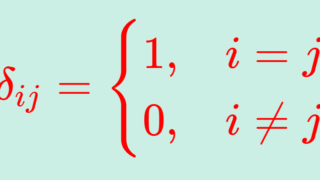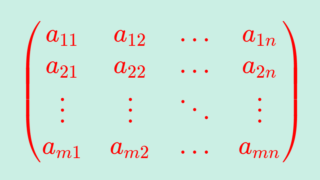線形代数学における最も基本的な概念の一つである,行列の基本的な定義について説明します。
行列とは
行列の定義
定義(行列)
a_{ij} \in \mathbb{R} とする。このとき,この要素を縦に m 個,横に n 個並べた
\color{red}\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix}の形のものを m \times n 行列 (matrix) または m 行 n 列の行列という。
行列は \ A, B, C のような大文字であらわされることが多く,A = (a_{ij}) のように略して書かれることが多い。
このとき, a_{ij} をその行列の (i, j) 成分という。
なお,簡単のため a_{ij} \in \mathbb{R} としましたが,実際には \mathbb{C} でも \mathbb{Q} でも構いません。
今回,行列の表記には丸括弧「()」を採用しましたが,四角括弧「[]」を採用して,
\color{red}\begin{bmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \\ \end{bmatrix}のように書くこともあります。まれに
\color{red}\begin{Bmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \\ \end{Bmatrix}のように書くこともあります。
ここで注意ですが, a_{ij} の添え字は,あくまで a_{i,j} と書くのが少々面倒でコンマを省いているだけのため, i \times j の意味ではありません。
なお,各成分が a_{ij} \in \mathbb{R} である m \times n 行列全体の集合を \color{red}M_{m,n}(\mathbb{R} ) と書くことがあります。別に今は覚えなくて良いです。
補足~どっちが行でどっちが列か~
\color{red} m \times n 行列,または \color{red}m 行 \color{red} n 列の行列と言ったときに,どっちが行でどっちが列か分からなくなることがあるかもしれません。これについては,以下の図のようになっています。
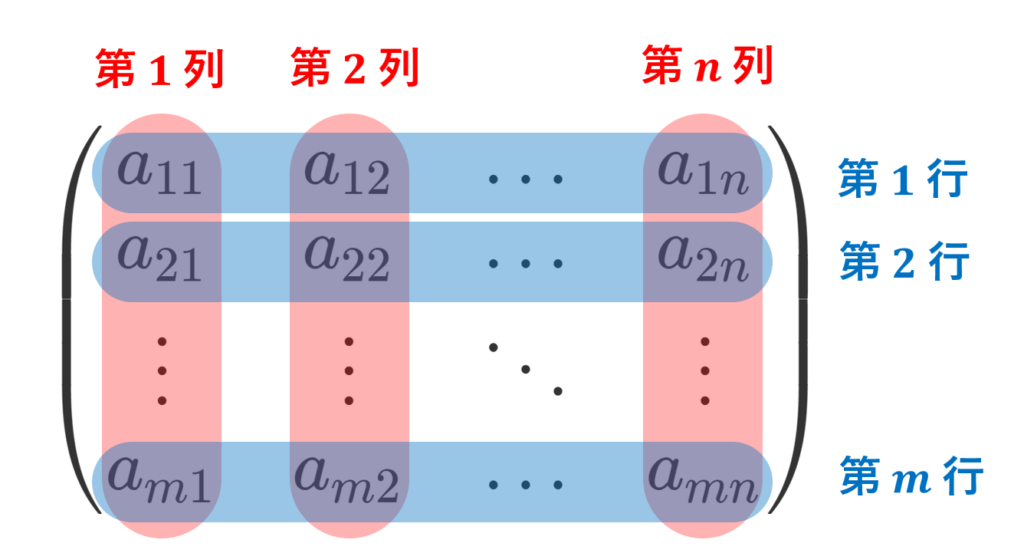
覚えておきましょう。
行列の例
簡単な例を挙げましょう。
行列の例
- \begin{pmatrix} 2 & 4 & 1 \\ 3 & 1 & 1 \end{pmatrix} は 2 \times 3 行列
- \begin{pmatrix} 1 & 3 \\ 2 & 3 \\ 0 & 0 \\ 0 & 4 \end{pmatrix} は 4 \times 2 行列
- \begin{pmatrix} 1 & 2 & 3 & 4 \end{pmatrix} は 1 \times 4 行列
- \begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix} は 3 \times 1 行列
正方行列とは
続いて正方行列を定義します。
正方行列の定義
定義(正方行列)
行列のうち,縦と横の成分の個数が同じ n 個のもの,すなわち \color{red} n \times n 行列を n 次正方行列 (square matrix) という。
n 次正方行列は
\color{red}\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \\ \end{pmatrix}の形である。
m \times n 行列において, m=n となるものを正方行列というんですね。
各成分が a_{ij} \in \mathbb{R} である n z次正方行列全体の集合を \color{red}M_{n}(\mathbb{R} ) と書くことがあります。これも今は覚えなくて良いです。
正方行列の例
正方行列の例
- \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix} は 2 次正方行列
- \begin{pmatrix} 3 & 1 & 4 \\ 2 & 5 & 5 \\ 12 & 0 & 1 \end{pmatrix} は 3 次正方行列
零行列とは
続いて零行列を定義しましょう。
零行列の定義
定義(零行列)
すべての成分が 0 である行列を零行列 (zero matrix, null matrix) という。
零行列は
\color{red}\begin{pmatrix} 0 & 0 & \ldots & 0 \\ 0 & 0 & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 0 \end{pmatrix}の形である。零行列は \boldsymbol{ 0} や O と書かれることが多い。
零行列の例
零行列の例
- \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} は 2 \times 3 の零行列
単位行列とは
最後に,単位行列の定義を確認しましょう。
単位行列の定義
定義(単位行列)
n 次正方行列において,(左上から右下への)対角成分のみ 1 でそれ以外は 0 である行列,すなわち
\color{red} a_{ij} = \begin{cases} 1 & i=j, \\ 0 & i \ne j \end{cases}となる行列を n 次単位行列 (identity matrix) という。
n 次単位行列は
\color{red}\begin{pmatrix} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 \end{pmatrix}の形である。 n 次単位行列は I, E や I_n, E_n と書かれることが多い。
単位行列は正方行列のみで定義されることに注意しましょう。
なお,単位行列における a_{ij} の定義は,クロネッカーのデルタの定義そのものです。クロネッカーのデルタを用いると, n 次正方行列は I_n = (\delta_{ij} ) と書けます。
単位行列の例
単位行列の例
- I_1 = \begin{pmatrix} 1 \\ \end{pmatrix} は 1 次の単位行列
- I_3 = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} は 3 次の単位行列
さらなる発展
行列の基本的な定義が分かったと思います。この先は,基本的な行列の演算を確認するとよいでしょう。これについては,以下の記事を参照してください。