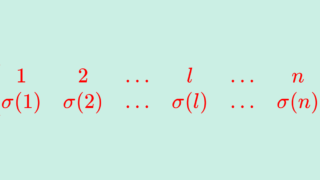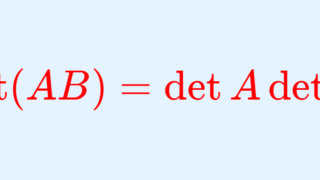正方行列に対して定義される「行列式」というスカラー量について,その定義と計算方法について解説します。
置換を用いた行列式(det)の定義
定義(行列式)
n 次正方行列 A =(a_{ij}) に対し,
\color{red} \det A = \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}
を行列式 (determinant) という。 A の行列式は,\color{red} \det A や \color{red} |A| などとかく。
ここで, S_n は置換全体を集めた対称群であり, \sum_{\sigma\in S_n} は,それら全部を足し合わせることを指します。
また, \operatorname{sgn} \sigma は置換の符号を指します。
行列式の具体例
2次正方行列の行列式
2次正方行列の行列式
\color{red}\begin{aligned} \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11} a_{22} - a_{12}a_{21}. \end{aligned}第1項・第2項の置換はそれぞれ \begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix} , \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} であり,置換の符号は 1, -1 となります。
3次正方行列の行列式
3次正方行列の行列式
\color{red}\begin{aligned} &\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \\ ={}& a_{11} a_{22}a_{33} - a_{11} a_{23}a_{32} \\ &+ a_{12}a_{23}a_{31} - a_{12}a_{21}a_{33} \\ &+ a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}. \end{aligned}各項の置換は順に
\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3\end{pmatrix},\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2\end{pmatrix}, \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1\end{pmatrix}, \\ \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3\end{pmatrix}, \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}, \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1\end{pmatrix}
に対応しています。3次の行列式は覚えなくてもよいですが,サラスの方法という暗記法があります。以下の記事を参照してください。
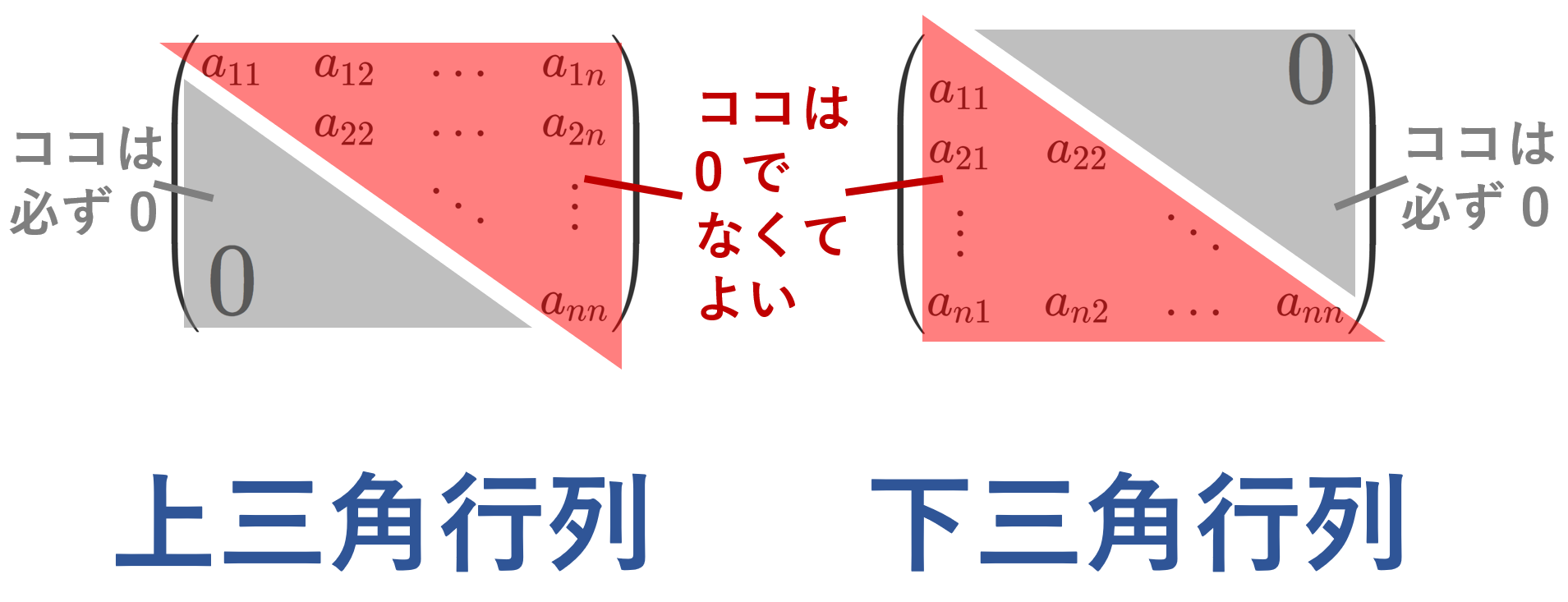
三角行列の行列式
三角行列の行列式
A = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ & a_{22} & \dots & a_{2n} \\ &&\ddots&\vdots \\ \huge{0}&&& a_{nn} \end{pmatrix}
の行列式は \color{red} \det A = a_{11}a_{22} \dots a_{nn} である。
下三角行列も同じである。
a_{11} a_{22} \dots a_{nn} 以外の項は積の中に必ず 0 が含まれるため,消えるわけです。
行列式の計算手順
行列式の計算は,もちろん定義通り計算しても構いません。しかし,たとえば 4 \times 4 行列の場合,足し算の数は 4! =24 個にもなってしまうため,あまり現実的ではありません。そこで,現実的な計算手順について,順を追って解説します。
行列式の現実的な計算手順
現実的な計算手順は,順に
- 行列の基本変形を用いて0を増やす(特に1行目or1列目)
- 1行目or1列目に注目して展開する
- 得られた小さな行列式に対して手順1-2を繰り返す
- 2次・3次または三角行列の行列式に帰着させ,計算する
です。それぞれ解説していきましょう。
1. 行列の基本変形を用いて0を増やす(特に1行目or1列目)
まずは行列の基本変形を用いて,1行目 or 1列目の成分がある程度 0 になるようにしましょう。行列の基本変形とは,次の3つの変形です。
- ある行(列)の \boldsymbol{c} 倍を他の行(列)に加えること
- 2つの行(列)を入れ替えること
- ある行(列)を \boldsymbol{ c \ne 0 } 倍すること
詳しくは,行列の基本変形についてわかりやすく図解するで解説しています。
基本変形をしたときの行列式は,以下のように変化します。
| 基本変形 | 行列式 |
|---|---|
| ある行(列)の {c} 倍を他の行(列)に加える | 変化なし |
| 2つの行(列)を入れ替える | \boldsymbol{-1} 倍 |
| ある行(列)を { c \ne 0 } 倍する | \boldsymbol{ c} 倍 |
このことを留意して,係数を調整しながら,ある程度計算しやすいところまで基本変形していきましょう。
注意ですが,このステップでは無理に計算しすぎなくて良いです。頑張って計算すれば三角行列にできるため,行列式が求まりますが,たとえば各成分に変数が含まれている場合,複雑な計算をすることになってしまうため,そこまでする必要はありません。ある程度同じ行・列に 0 が集まればOKと思い,次のステップに進みましょう。
2. 1行目or1列目に注目して展開する
行列式には,以下のような性質があります。
定理(行列式に関する等式)
A を n 次正方行列とする。
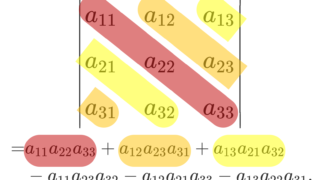
A_{ij} を A から i 行と j 列を取り除いた n-1 次正方行列の行列式とすると,
(-1)^{i+j} A_{ij} を余因子と言います。これを図にすると,以下のようになります。
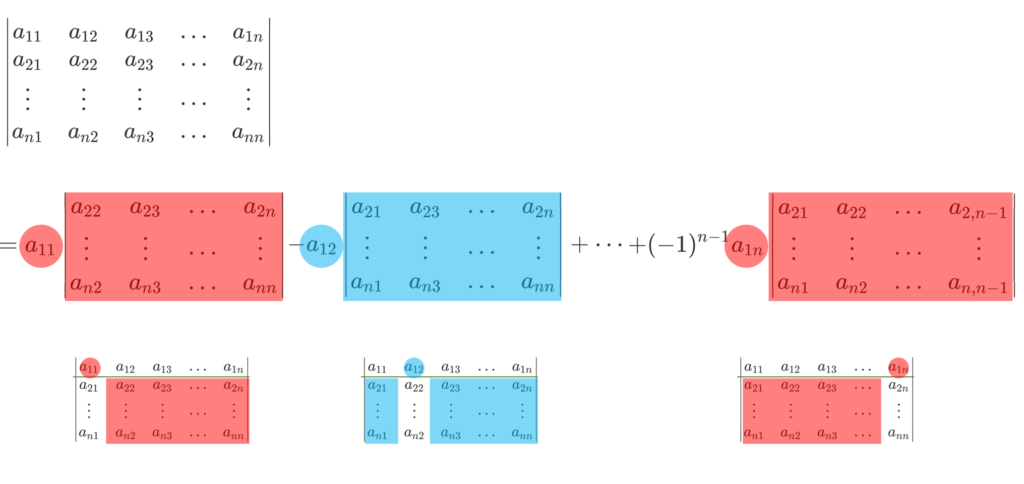
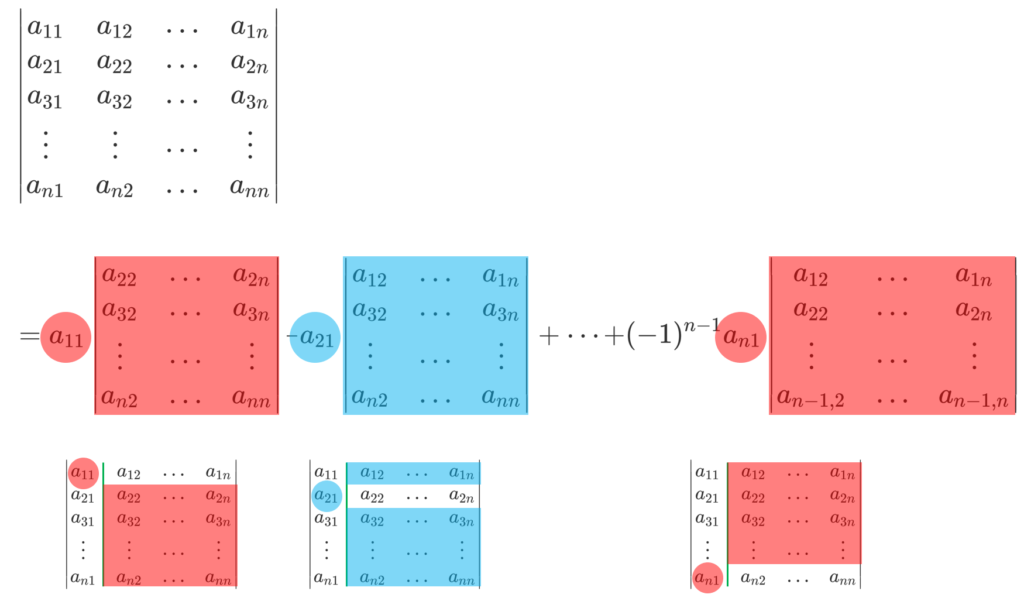
これ自身の証明は,余因子行列の定義と余因子展開~逆行列になる証明~で行っています。これを用いて,行列式を展開しましょう。
このとき,手順1の効果で, a_{1j} = 0 (または a_{i1} = 0 ) の項は消えますね。
なお,一般に1行目or1列目以外の行・列に注目して展開することも可能ですが,手順1で「2つの行(列)を入れ替えること」を行って,1行目or1列目に移動させてから展開すると考えればよいでしょう。
3. 得られた小さな行列式に対して手順1-2を繰り返す
手順2を行うと,小さな行列式がたくさん出てくると思います。これについて,再び手順1-2を繰り返しましょう。
4. 2次・3次または三角行列の行列式に帰着させ,計算する
2次・3次・三角行列の行列式にしてしまえば,具体例のところで挙げたとおり,計算できますね。
長いステップですが,実際に手計算するのは3次から5次程度の行列式だと思うので,「何度も手順1-2を繰り返さねばならない」ということはないでしょう。
行列式の計算の例題
実際に,以下の問題に取り組んでみましょう。
例題
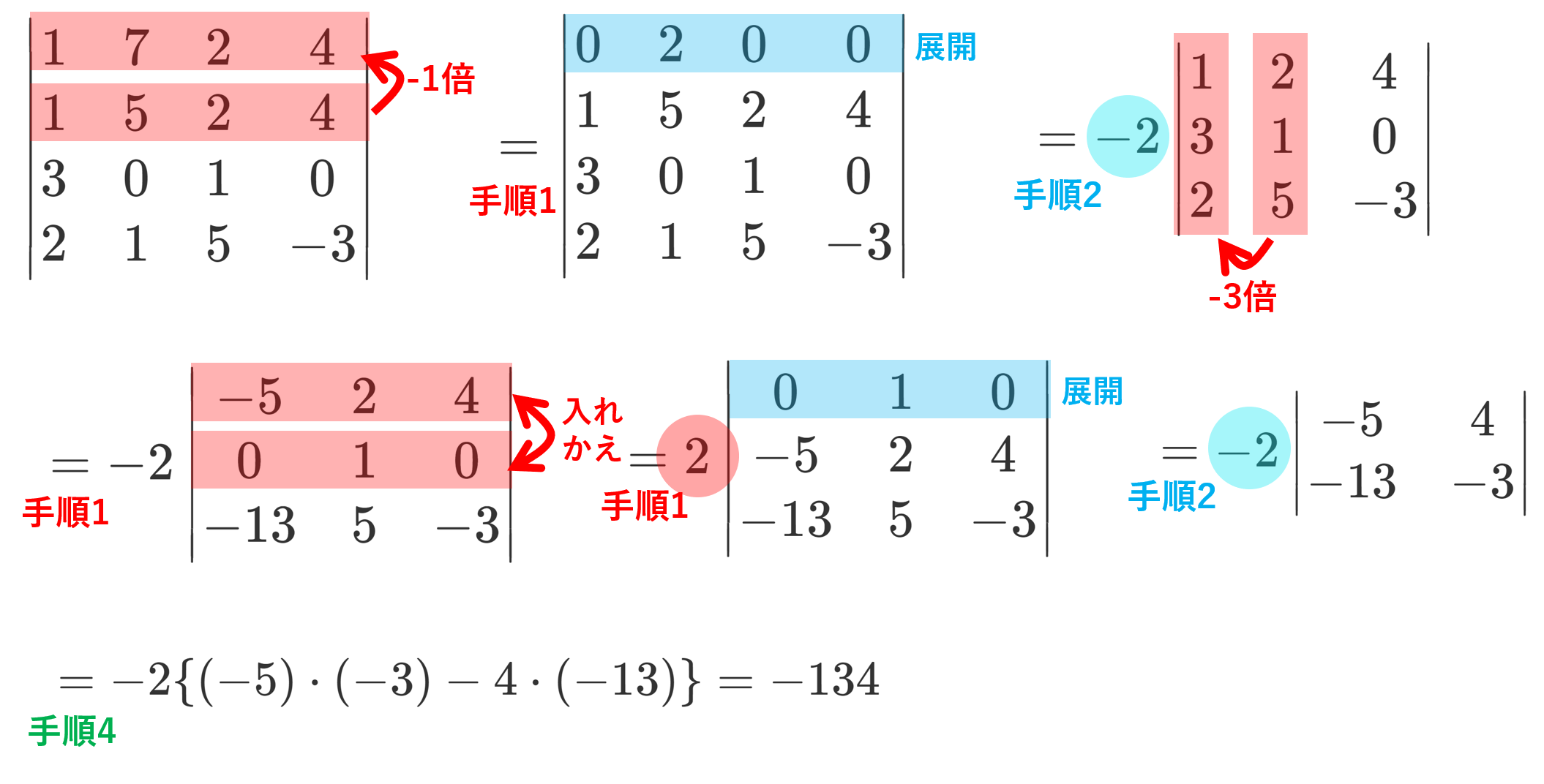
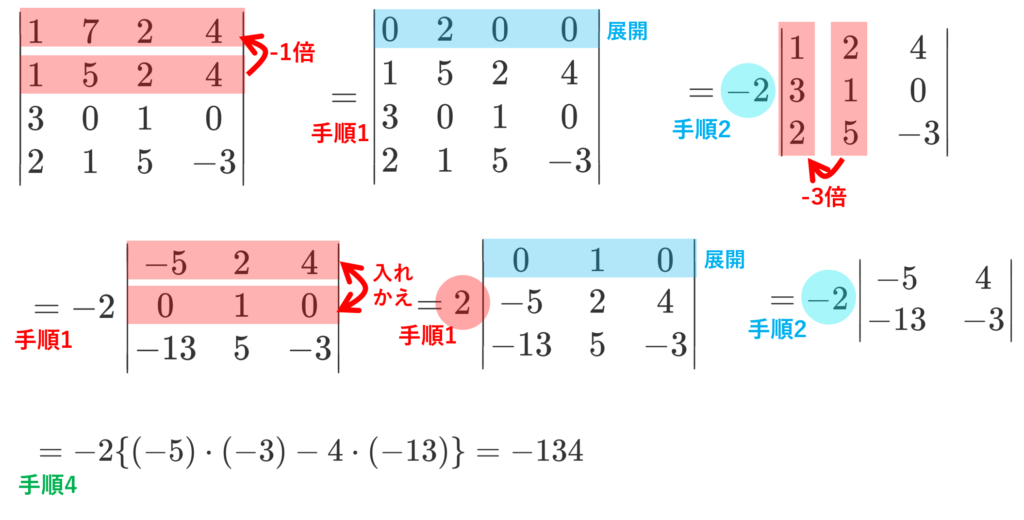
\color{red} \begin{vmatrix} 1 & 7 & 2 &4 \\ 1 & 5 & 2 & 4 \\ 3 & 0 & 1 & 0 \\ 2 & 1 & 5 & -3 \\ \end{vmatrix} を計算せよ。
計算手順を復習すると,
- 行列の基本変形を用いて0を増やす(特に1行目or1列目)
- 1行目or1列目に注目して展開する
- 得られた小さな行列式に対して手順1-2を繰り返す
- 2次・3次または三角行列の行列式に帰着させ,計算する
でした。これを用いて手順通りに計算すると,解答例は以下のようになります。最短手順とは限らず,別の変形をしても構いません。係数に気を付けましょう。
本記事では,例は一つしか紹介しませんが,もっと多くの例を知りたい場合は,たとえば固有値の定義と求め方をていねいに~計算の手順~の例題も見てみてください。
「固有値」の概念は,現時点で分かる必要はないですが,計算例題は,結局「変数を含む行列式の計算」ですから,そこは理解できるでしょう。
計算機やコンピューターを利用するのもアリ
数学科の学生が行列式を手計算するのは,線形代数のテストや院試のときくらいです(もちろん,計算機で計算できない抽象的な行列を研究する場合はその限りでないです)。
応用数学の研究などでは,計算機を用いて計算するのが一般的です。たとえば,WolframAlphaを用いれば,インターネット上でも計算することができます。本格的に計算するためには,MathematicaやPython, Julia, R, Fortran, Mapleなどのプログラミング言語を利用すればよいでしょう。
行列式の性質
行列式の性質は,以下が有名です。
以下で,複素数 \mathbb{C} は実数 \mathbb{R} に変えても成立します。
定理(行列式の性質)
1. 行列式は,各列に関して線形性がある。すなわち, \boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n を n 次元列ベクトル, s,t\in \mathbb{C} とすると,
\small \begin{aligned} &\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{s\boldsymbol{a_k}+t\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\ ={}&\textcolor{red}{s} \det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{a_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\ &+ \textcolor{red}{t}\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}). \end{aligned}
また同様に,行列式は各行に関して線形性がある。すなわち, \boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n を n 次元行ベクトル, s,t\in \mathbb{C} とすると,
2. 転置行列の行列式は元のそれと同じ。すなわち, \color{red}\det A = \det A^\top.
3. (列・行の入れ替え) \sigma\in S_n を置換とする。このとき,太字を列ベクトルとすると,
\begin{aligned}& \det(\boldsymbol{a_{\textcolor{red}{\sigma(1)}}}, \dots ,\boldsymbol{a_{\textcolor{red}{\sigma(n)}}})\\ & =\textcolor{red}{( \operatorname{sgn} \sigma )}\det(\boldsymbol{a_1}, \dots,\boldsymbol{a_n}).\end{aligned}
太字を行ベクトルとすると,
特に, 2つの列(または行)を入れ替えると,行列式は \color{red} -1 倍になる。
4. 2つの列(または行)が等しい行列式の値は \color{red} 0 である。
5. 行列式と積は可換である。すなわち, A,B を n 次正方行列とするとき,
\color{red} \det (AB) = \det A \det B.
6. A が正則のとき, \color{red}\det (A^{-1}) = (\det A)^{-1} .
これらの証明については,以下の記事を参照してください。
おわりに
行列式の計算は,線形代数学のテストで頻出です。しっかりと演習を積んで,テストに臨みましょう。