n 次正方行列 A, B が相似であるとは,ある n 次正則行列(すなわち逆行列が存在する行列) P が存在して, B=P^{-1}AP となることを指します。
これについて,その定義と線形写像の表現行列との関係性,性質とその証明を解説します。
行列の相似の定義
定義(行列の相似)
A,B を n 次正方行列とする。 A と B が相似 (similar) であるとは,ある正則行列(可逆行列) P が存在して,
\color{red} \large B=P^{-1} AP
と表せることである。本記事では,これを \color{red} A\sim B とかくことにする。
行列の相似は「行列の対角化」など,さまざまなところに出てくる基本的概念の1つです。定義は覚えましょう。
なお,2つの行列があったときに,それが相似であるか判定するには,どちらもジョルダン標準形と呼ばれる形に変形してあげるとよいです。
行列の相似の線形代数的意味
ここで,「なんで相似なんか考えるの」という疑問を持ったかもしれません。そこで,相似のベクトル空間的意味を考えましょう。
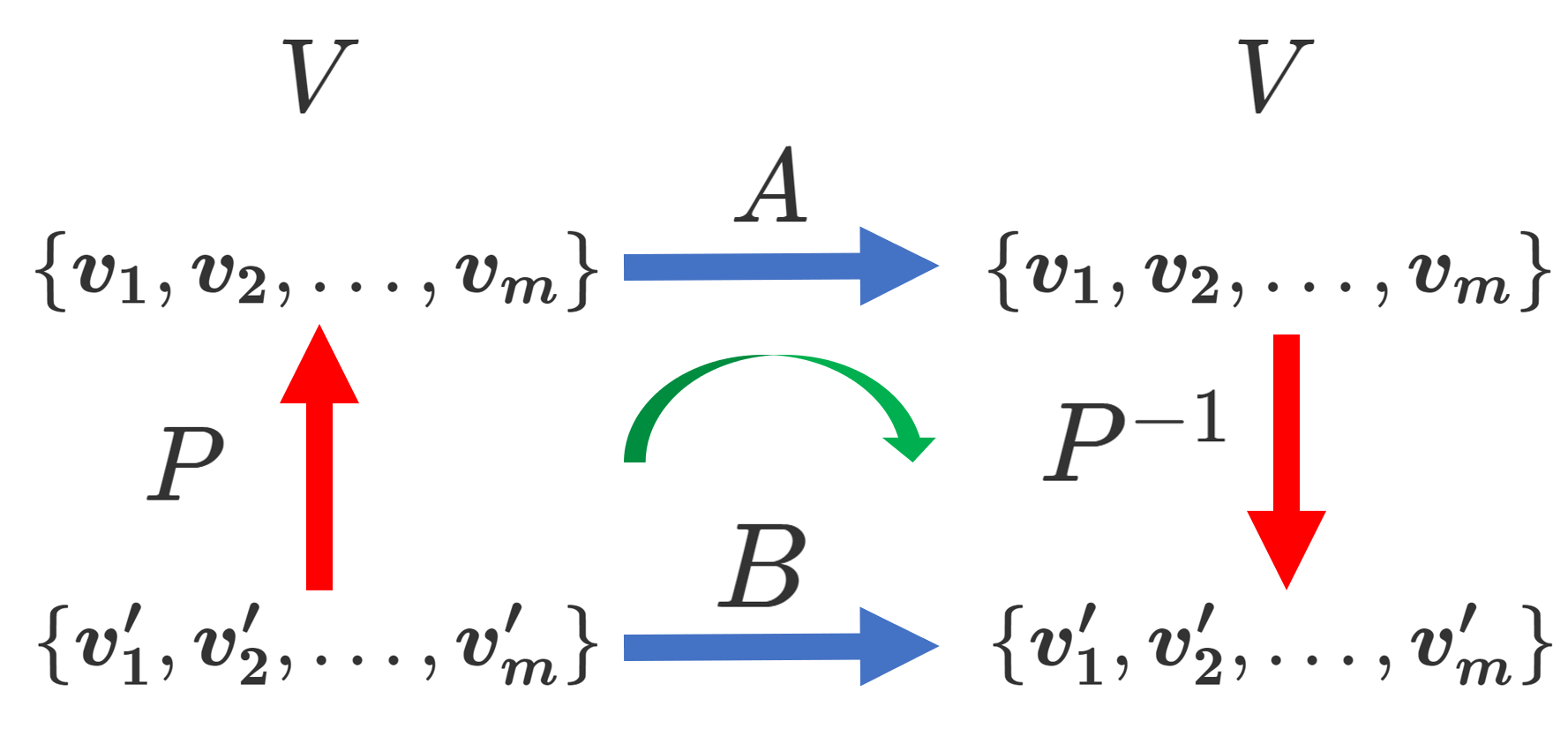
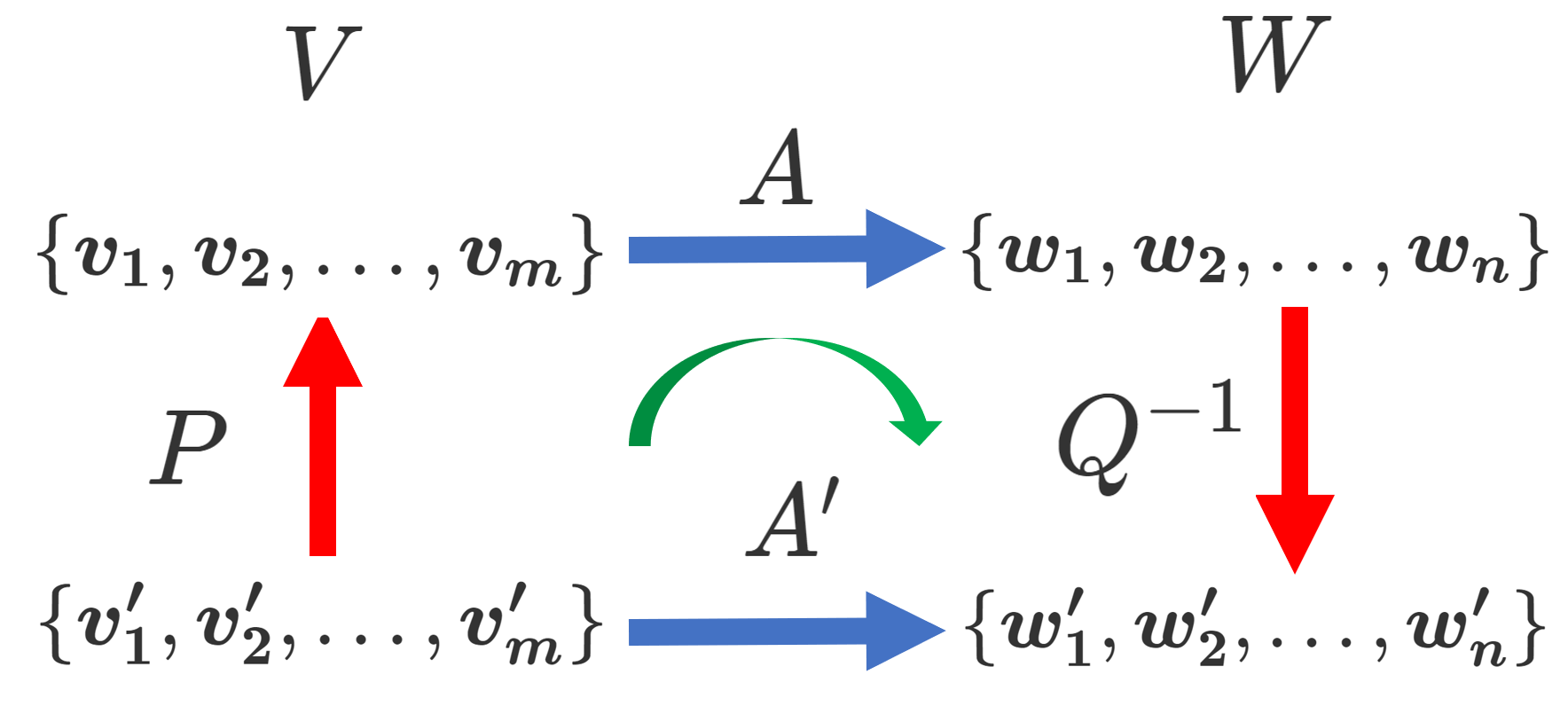
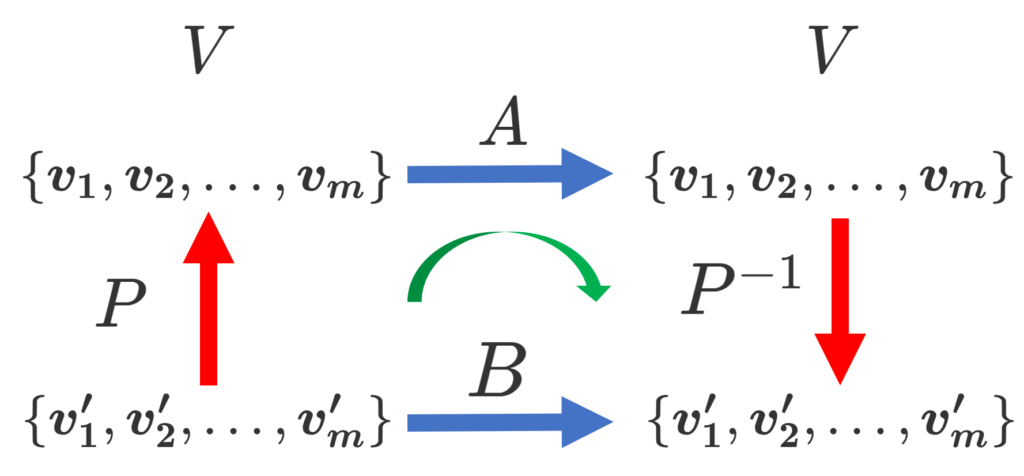
行列は,線形写像の表現とみることができます。特に, A は正方行列ですから, n 次元ベクトル空間 V 上の線形写像 f\colon V\to V の,ある基底 \{ \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_n}\} に関する表現行列と見ることができます(→【表現行列】線形写像の行列表示を詳しく)。
一方で,\{ \boldsymbol{v'_1}, \boldsymbol{v'_2},\dots, \boldsymbol{v'_n}\} を別の基底とし, P を
(\boldsymbol{v'_1}, \boldsymbol{v'_2},\dots, \boldsymbol{v'_n}) = (\boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_n})P
となる基底の変換行列としましょう。
このとき, B = P^{-1} AP は f の, 基底 \{ \boldsymbol{v'_1}, \boldsymbol{v'_2},\dots, \boldsymbol{v'_n}\} に関する表現行列に相当します。
この証明含め,詳しくは以下の記事を参照してください。
基底の取り方を工夫すれば,同じ線形写像から,簡易な行列表示を得ることができます。相似な行列を考えて,簡易な行列と相似にさせることで,できるだけ線形写像を簡便に捉えようという試みに繋がるわけです。
行列の相似の性質
行列の相似には,覚えるべき良い性質がたくさんあります。紹介しましょう。本記事では相似を A\sim B とかき表すことを思い出してください。
定理(行列の相似の性質)
相似は不変量が多く,良い性質をもちますね。ひとつずつ証明していきましょう。
1. 同値関係について
証明
1-1. A = I^{-1}AI ( I は単位行列) より, A\sim A である。
1-2. B = P^{-1}AP と仮定する。このとき, Q=P^{-1} とすると, B = QAQ^{-1} であり,両辺の左から Q^{-1},右から Q をかけることで,
Q^{-1}BQ = A.
これは, B\sim A を意味する。
1-3. B= P^{-1}AP,\; C = Q^{-1}B Q とすると,
\begin{aligned}C&= Q^{-1}B Q \\ &= Q^{-1} P^{-1}AP Q = (PQ)^{-1} A (PQ)\end{aligned}
これは, A\sim C を意味する。
証明終
2-1. det A = det B について
証明
\det (AB) = \det A \det B,\; \det (A^{-1}) = (\det A)^{-1} である(→行列式の性質6つの証明(列,行の線形性,置換,積,転置など))。これを用いると,
\begin{aligned}\det B &= \det (P^{-1}AP) \\&= \det (P^{-1}) \det A \det P \\ &= (\det P)^{-1} \det A \det P\\ &= \det A. \end{aligned}証明終
2-2. rank A = rank B について
証明
正則行列をかけても,元の行列のランクは変わらないから, \operatorname{rank} A=\operatorname{rank}B である。
証明終
2-3. tr A = tr B について
証明
トレースは,その行列の固有値の和になる(→行列のトレース(tr)とは~定義と性質とその証明~)。よって,2-4.より, \operatorname{tr} A =\operatorname{tr} B である。
証明終
2-4. 固有値の一致について
証明
B の固有値は \det (B-\lambda I) の解 \lambda である(→固有値の定義と求め方をていねいに~計算の手順~)。ここで,
\begin{aligned} \det (B-\lambda I) &= \det (P^{-1}AP - \lambda I) \\ &= \det (P^{-1} (A-\lambda I ) P) \\ &= (\det P)^{-1} \det (A-\lambda I) \det P \\ &= \det (A-\lambda I)\end{aligned}
であるから, この解 \lambda は A の固有値でもある。よって,両者の固有値は一致する。
証明終
2-5. A^n ~ B^n について
証明
B = P^{-1} AP とする。このとき,
\begin{aligned} B^n &= ( P^{-1} AP )^n \\ &= (P^{-1} AP )( P^{-1} AP )\dots ( P^{-1} AP ) \\ &= P^{-1} A(P P^{-1}) A(PP^{-1}) \dots (P P^{-1} )AP \\ &= P^{-1} A^n P\end{aligned}
であるから, B^n = P^{-1}A^n P より, A^n と B^n は相似である。
証明終
無事に証明できましたね。