「上に有界な単調増加数列」あるいは「下に有界な単調減少数列」は収束するという定理は,高校数学で証明なしに用いた定理の1つでしょう。これは,実数の連続性と数列の極限を厳密に定義する \varepsilon \text{-} N 論法を用いて証明されます。これについて紹介しましょう。
定理の主張~有界な単調増加列の収束~
定理(上に有界な単調増加数列は収束する)
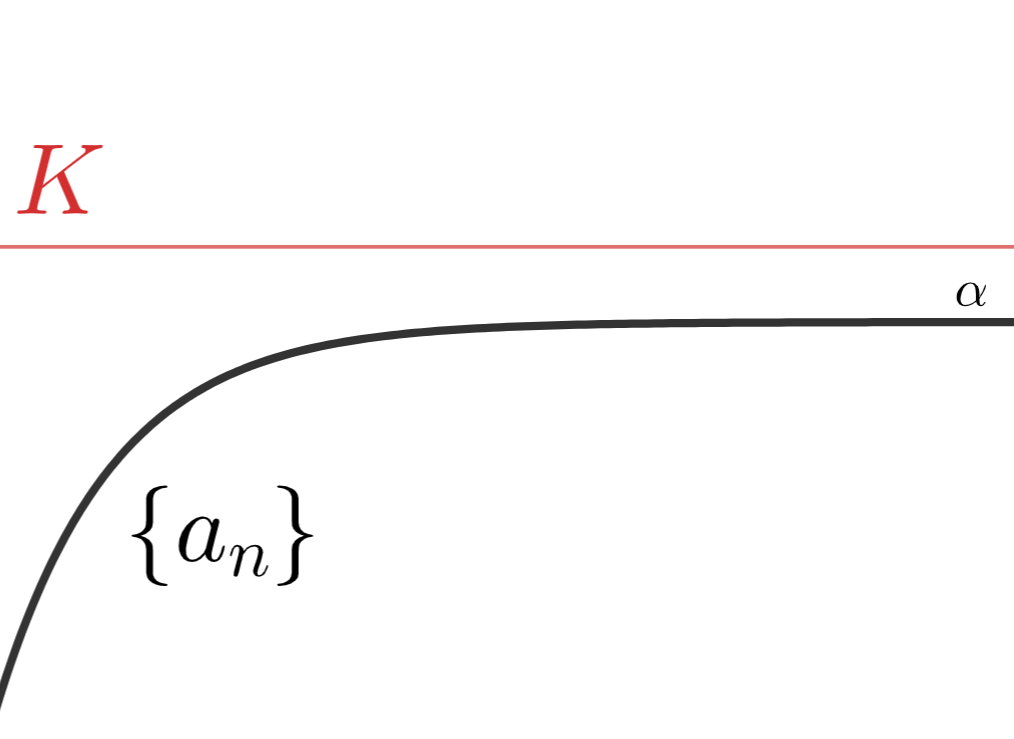
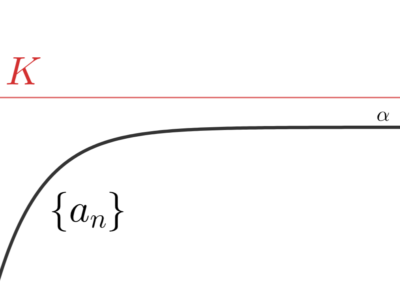
実数の数列 \{a_n\} は(広義)単調増加(すなわち \color{red} a_n \le a_{n+1} )とし,かつ上に有界(すなわち \color{red} a_n < K ) とする。
このとき,この数列は収束する。
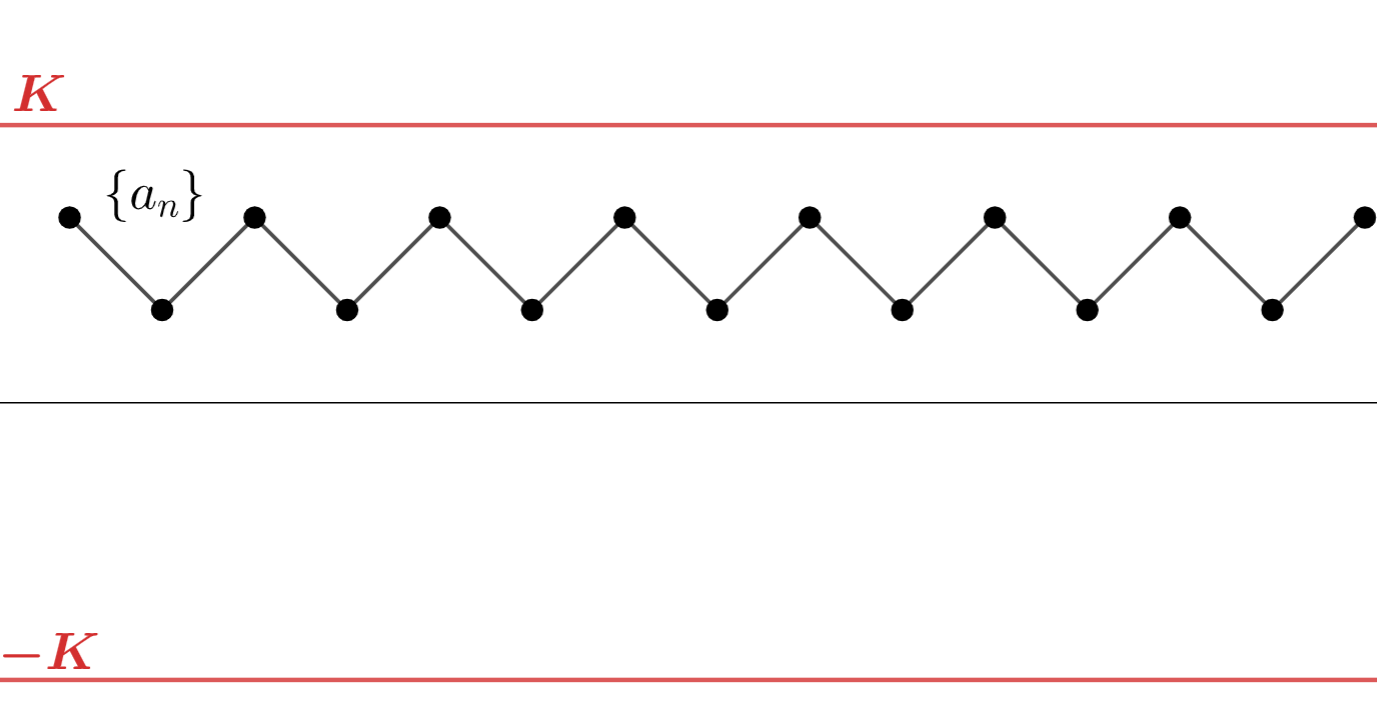
なお, \{-a_n\} を考えることで,下に有界な単調減少数列が収束することもわかります。
早速証明しましょう。
証明
証明
上に有界なので,\alpha = \sup\{a_n \mid n \ge 1\} <\infty と定める。
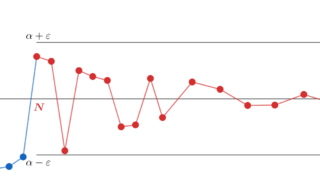
\sup の定義より,任意の \varepsilon > 0 に対して,ある N \ge 1 が存在して,
a_N > \alpha-\varepsilon
が成り立つ(→上限,下限(sup,inf)の定義と最大,最小(max,min)との違い)。式変形して, 0\le \alpha- a_N < \varepsilon となる。
\{a_n \} は単調増加であったから,
である。これは, \lim_{n\to\infty} a_n = \alpha を意味する。
証明終
最初の, \sup の存在は実数の連続性により保証されますから,実数の連続性が深く関係していることが分かります(→デデキント切断による実数の構成を解説)。
最後は,数列の極限の定義を使っています。これについては以下の記事で詳細に解説していますから,参照してください。
「収束の基本的なこと」に関する他の話題
- イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~
- イプシロンデルタ論法をわかりやすく丁寧に~関数の極限の定義~
- 極限の性質6つの証明(一意性,和,積,商,大小関係)
- 収束する数列は有界であることの証明
- はさみうちの原理とその厳密な証明~数列版・関数版~
- 追い出しの原理とその厳密な証明~数列版・関数版~
- 実数上関数の収束と数列の収束の同値性とその証明
- ボルツァノ–ワイエルシュトラスの定理とその証明
- 【チェザロ平均】数列が収束するとき平均も同じ値に収束する証明
- 【微分積分学】コーシー列とは~定義と収束性の証明~