 記号・記法
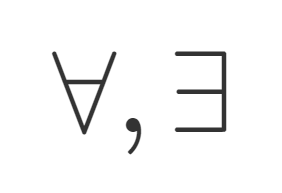
記号・記法 ∀(全称記号,任意の)と∃(存在記号,存在する)の使い方
大学数学の授業やセミナー,ときどき論文や教科書でも使われる記号である,∀(任意の)と∃(存在する)は,それぞれ「全称記号」「存在記号」といわれます。これについて,その使い方を,具体例を交えて解説します。
 記号・記法
記号・記法 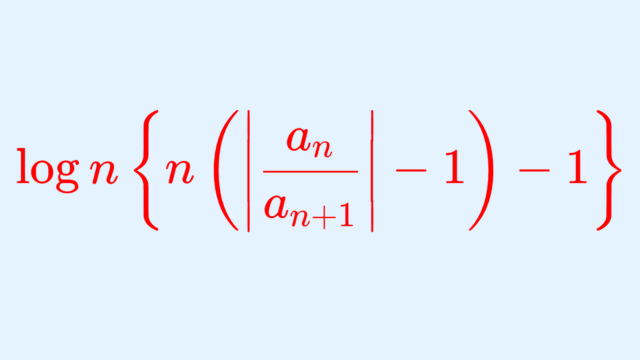 微分積分学(大学)
微分積分学(大学) 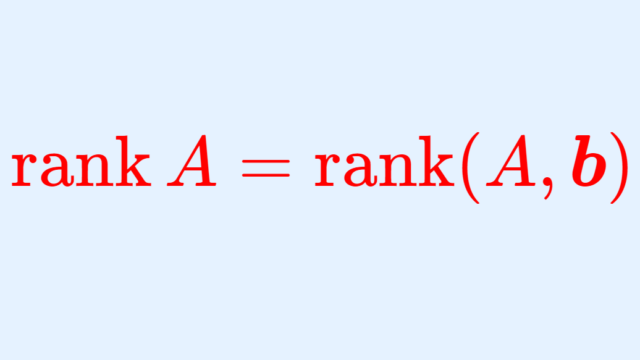 線形代数学
線形代数学 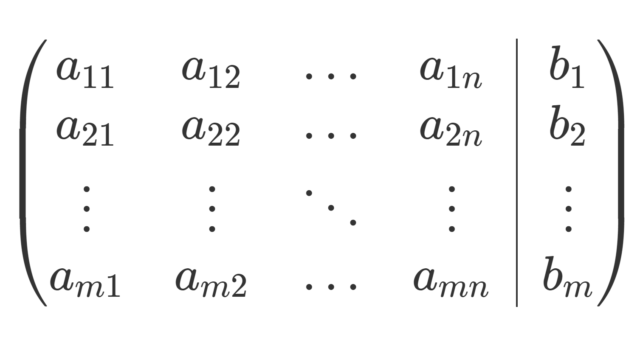 線形代数学
線形代数学 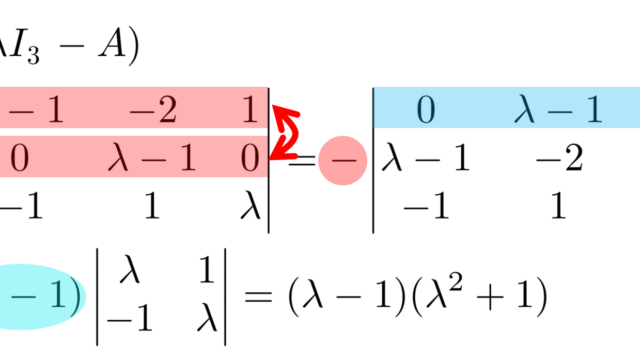 線形代数学
線形代数学 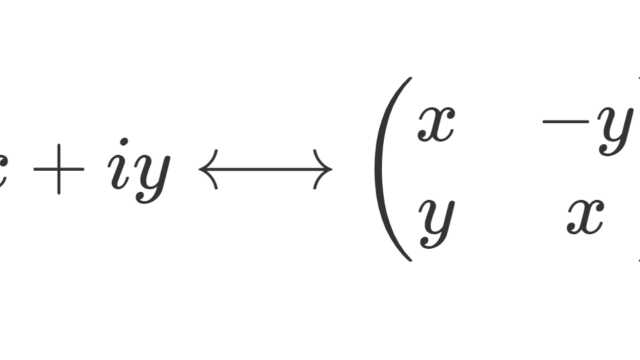 線形代数学
線形代数学 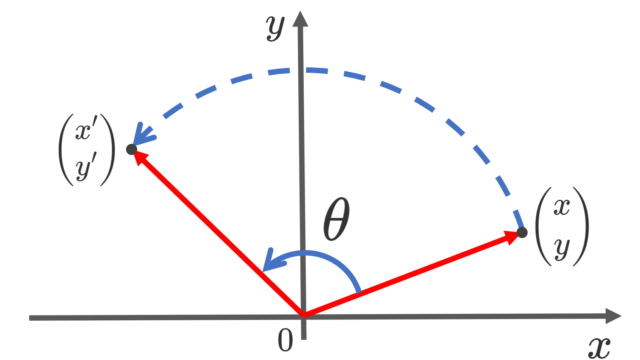 線形代数学
線形代数学 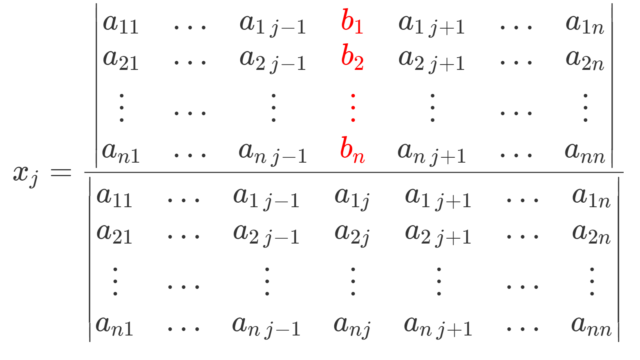 線形代数学
線形代数学 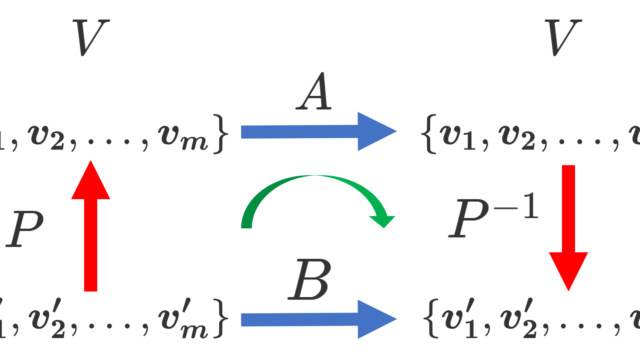 線形代数学
線形代数学 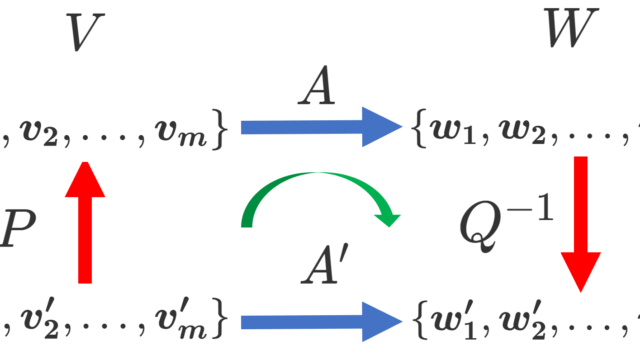 線形代数学
線形代数学