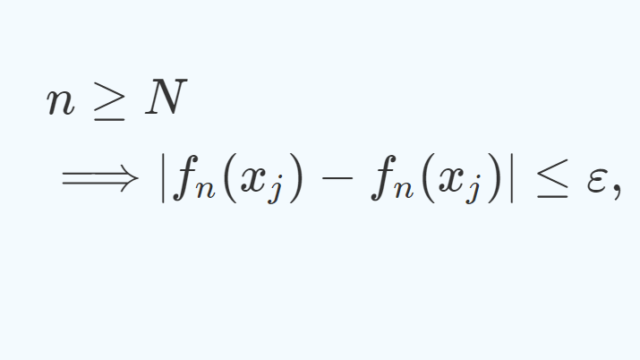 微分積分学(大学)
微分積分学(大学) 閉区間上各点収束列が同程度連続ならば一様収束することの証明
関数列が各点収束するとき,同程度連続であれば,それが一様収束であるという定理を紹介し,証明します。 \{f_n\colon [0, 1] \to \mathbb{R} を同程度連続な関数列とし,f \colon [0, 1] \to \mathbb{R}に各点収束するなら,この収束は一様収束である。
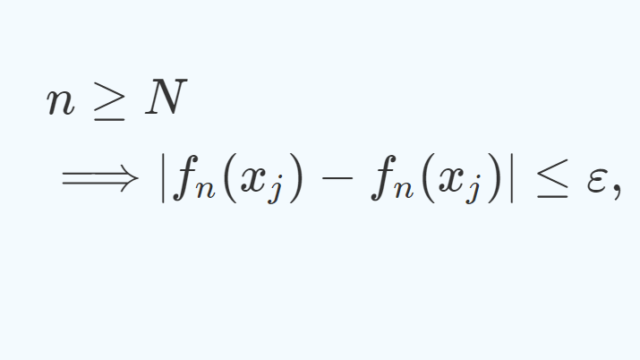 微分積分学(大学)
微分積分学(大学)  LaTeX
LaTeX 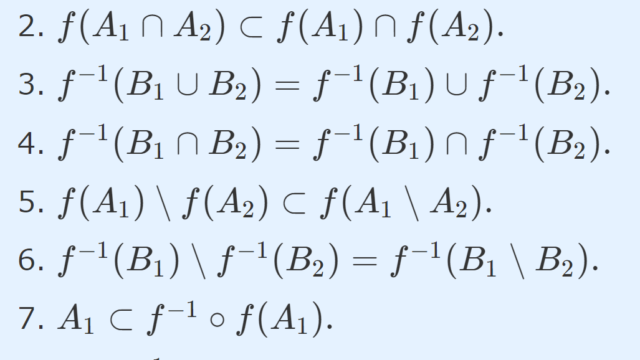 集合と位相
集合と位相 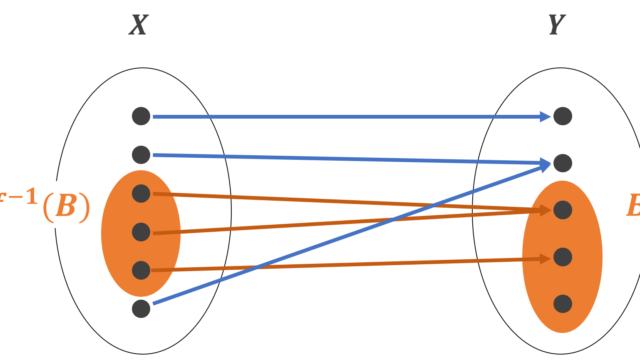 記号・記法
記号・記法 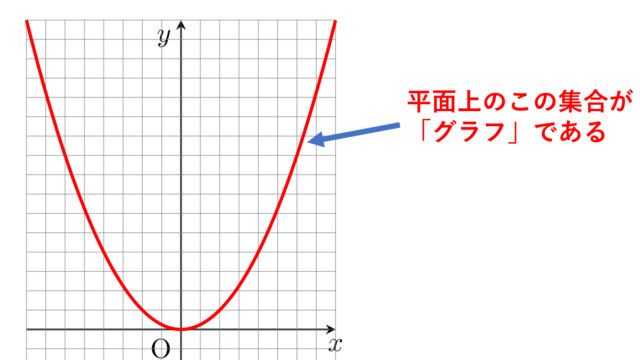 記号・記法
記号・記法 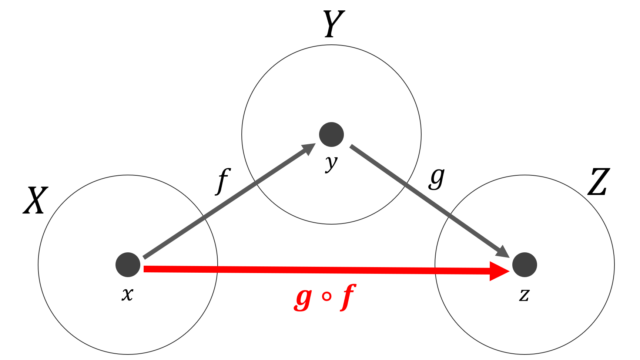 記号・記法
記号・記法 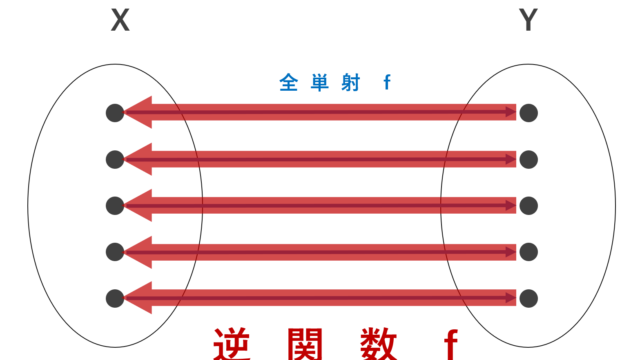 記号・記法
記号・記法 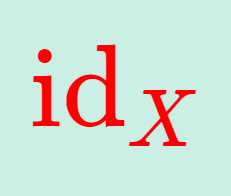 記号・記法
記号・記法  記号・記法
記号・記法  記号・記法
記号・記法