 English
English 【数学英語】略語まとめ
授業やセミナーといった「ラフ」な場面でよく用いられる,数学英語における共通の「略語」を紹介します。なお,自身の身の回りのものを反映しているため,人によって流儀が違う可能性があります。変なものがありましたらお知らせください。
 English
English 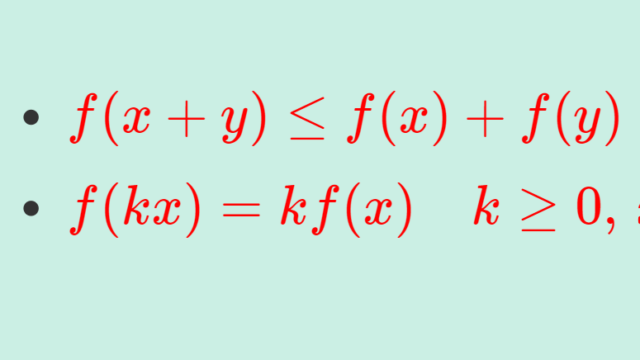 解析学(大学)その他
解析学(大学)その他 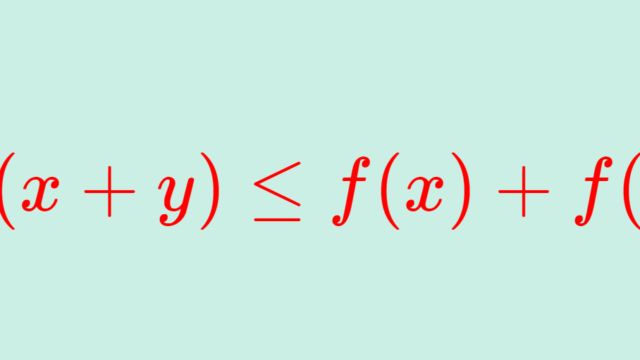 解析学(大学)その他
解析学(大学)その他 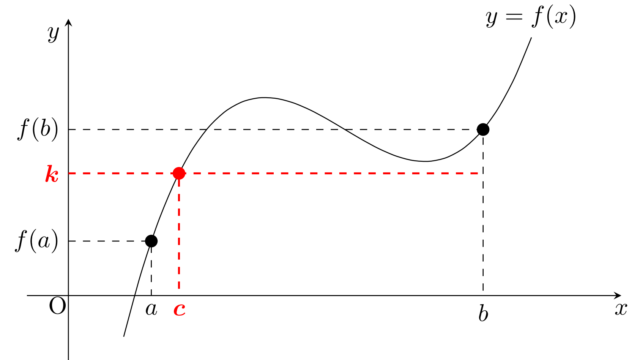 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  記号・記法
記号・記法 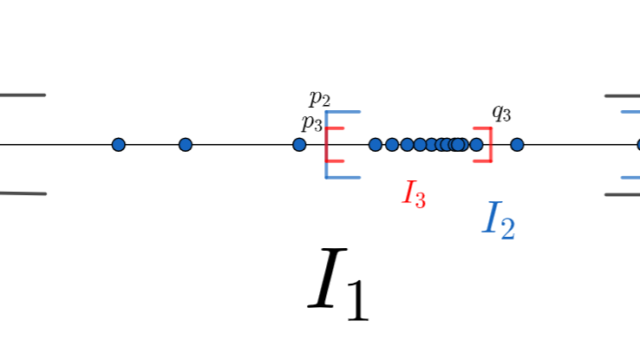 微分積分学(大学)
微分積分学(大学) 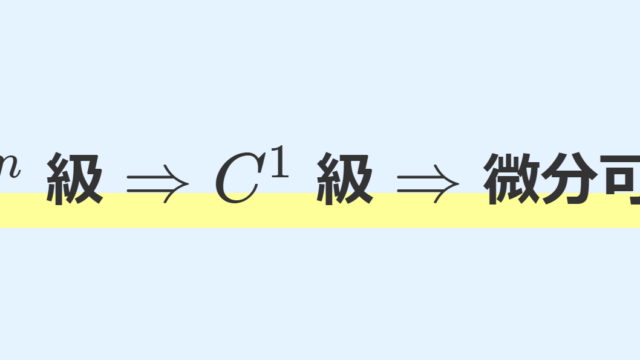 微分積分学(大学)
微分積分学(大学) 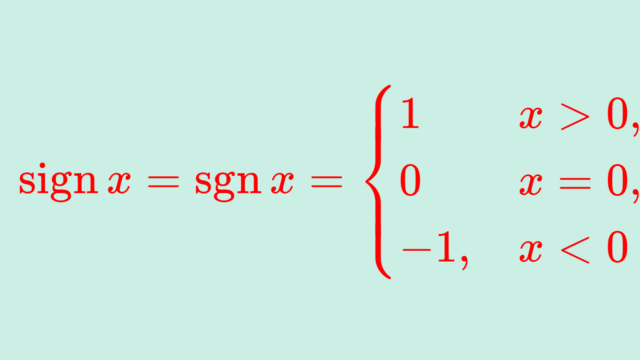 記号・記法
記号・記法 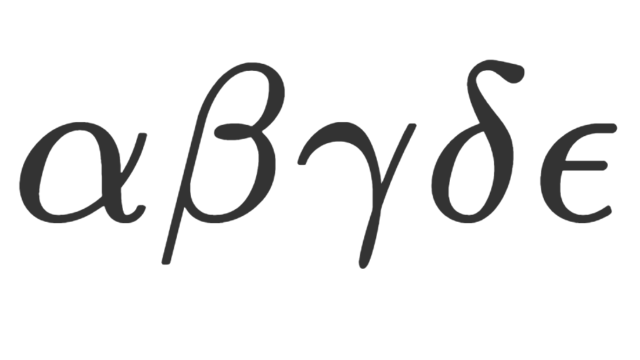 LaTeX
LaTeX