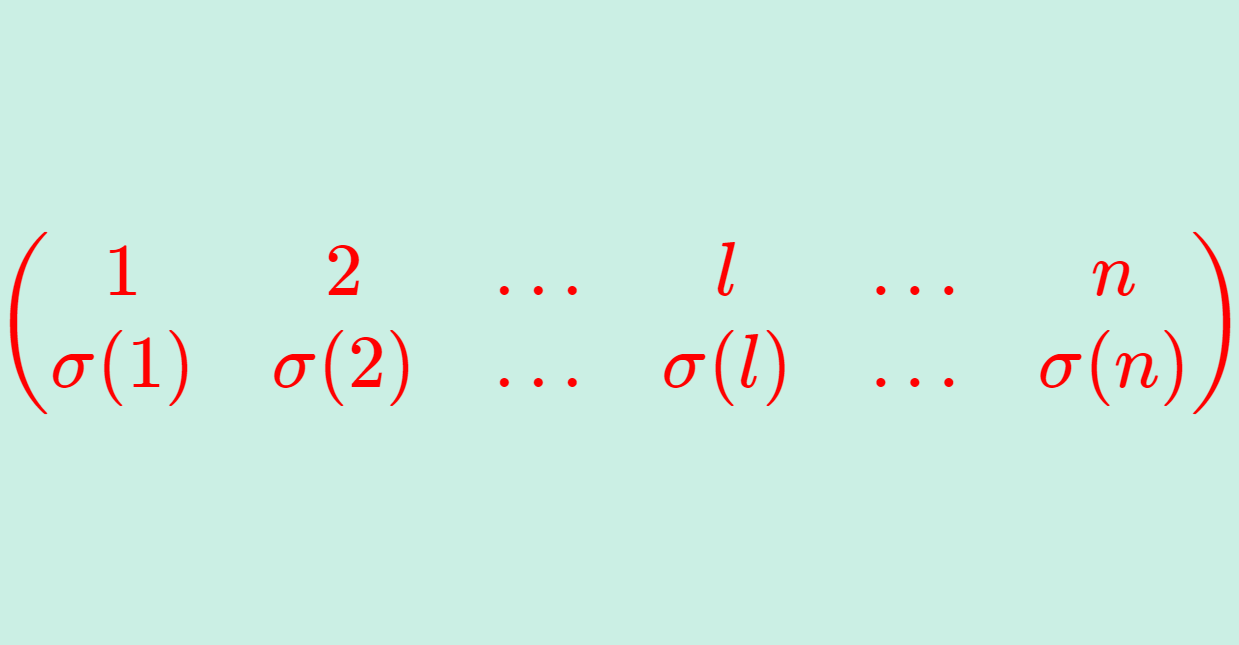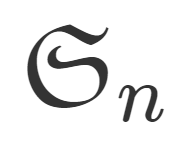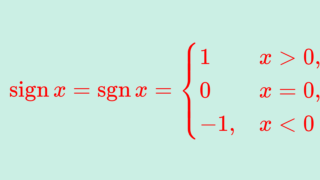線形代数学や群論において登場する「置換」について,特に線形代数の行列式を定義するにあたって必要な知識のみをまとめて解説します。
置換とその積
まずは,置換とその積について定義し,具体例を述べます。
置換とその積の定義
定義(置換・置換の積)
\sigma\colon \{1,2,\ldots, n\} \to \{1,2,\ldots, n\} が全単射のとき,この写像を置換 (permutation) という。
置換は
のように表現される。(これを置換行列 (permutation matrix) という。)
二つの置換 \sigma_1, \sigma_2\colon \{1,2,\ldots, n\} \to \{1,2,\ldots, n\} に対し,その合成写像なる置換 \sigma_2 \circ \sigma_1 を \sigma_1, \sigma_2 の積 (product) といい,単に \color{red} \sigma_2\sigma_1 と表す( \sigma_1\sigma_2 と表す流儀もある)。
置換は並び替えといえます。実際,並び替えを表すのに置換を用いて表現することが多いです。
置換の表現は, l \mapsto \sigma(l) をタテに書いて羅列したものだと思えますね。これは行列と同じ表記ですが,意味が異なります。
なお,一般の有限集合 X に対しても,番号付けすることで,置換 \sigma\colon X \to X を考えることが可能です。
置換とその積の具体例
置換の例とその積の例を見ておきましょう。
置換の例
\sigma \{1,2,3\} \to \{1,2,3\} を \sigma(1) = 3, \sigma(2)=2, \sigma(3)=1 と定めると,これは全単射なので置換であり,
\begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}
と表現できる。
置換の積の例
\sigma_1 = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}, \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} と定めると,
\sigma_2\sigma_1 = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}, \sigma_1\sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1& 3 \end{pmatrix}
となる。
積は「写像の合成」ですから,右から計算することに注意してください。
なお上の例のように,置換は一般の写像と同じく,非可換です。すなわち,一般には \color{red} \sigma_1\sigma_2 \ne \sigma_2\sigma_1 となります。
対称群
n 個のものの「並び替え」は全部で n! 通りありますから,置換 \sigma の取り方も n! 通りあります。これら全体の集合を n 次対称群 (symmetric group) といい, \color{red} S_n や \color{red} \mathfrak{S}_n という記号で表します。
対称「群」といわれるのは,代数学で言う「群論」と関係しているからですが,そこまでの知識は必要ありません。今大切なのは,「置換は全部で n! 個あり,それら全体の集合を考えることができる」点です。
対称群については,以下で解説しています。
逆置換
置換は定義域と値域が等しい全単射であったため,逆写像もまた置換になります。これを逆置換と言います。
定義(逆置換)
置換 \sigma\colon \{1,2,\ldots, n\} \to \{1,2,\ldots, n\} に対し, \sigma^{-1} \colon \{1,2,\ldots, n\} \to \{1,2,\ldots, n\} を \sigma の逆置換 (inverse permutation) という。
逆置換は,置換による「並び替え」を逆再生したものと言えます。
互換
続いて,置換のうち特に「互換」と呼ばれるものについて定義し,性質を述べましょう。
互換の定義
定義(互換)
置換のうち,2つの元のみを入れ替えた置換,すなわち 1\le i < j \le n に対し,
\color{red} \sigma(i) =j, \; \sigma(j)= i, \;\sigma(l) = l \, (l\ne i, j)
となる置換,あるいは置換の表記法を用いて
となる置換を互換 (transposition) という。互換は,交換する元が i, j のとき, \color{red}(i, j ) とかいて表す。
互換は (i,j) の代わりに (ij) とかくこともあります。
なお,より一般に異なる 1\le i_1, i_2, \dots, i_m \le n に対し, i_1\mapsto i_2\mapsto i_3 \mapsto \dots \mapsto i_m \mapsto i_1 となる置換を長さ m の巡回置換 (cyclic permutation) といい, (i_1, i_2, \dots, i_m) と書いて表します。
任意の置換は互換の積で書ける
次の定理が知られています。
定理(置換は互換の積で書ける)
\sigma を置換とすると,ある互換 \tau_1, \tau_2, \ldots , \tau_m が存在して, \color{red}\sigma=\tau_m\tau_{m-1}\dots\tau_1 と書ける。
「並び替え」で考えると,全体の「並び替え」は,2つずつの「並び替え」を複数回行うことで得られると言っていることになります。感覚的には正しそうですね。
例を一つ挙げると,
\begin{pmatrix}1 & 2& 3 \\ 3 & 1 & 2 \end{pmatrix}= (2, 3)(1,2)
となります。実際, 1 \mapsto 2 \mapsto 3, 2\mapsto 1 \mapsto 1, 3\mapsto 3\mapsto 2 となって, \begin{pmatrix}1 & 2& 3 \\ 3 & 1 & 2 \end{pmatrix} が得られました(互換の積は右から計算することに注意)。
略称をしておきましょう。
略証
置換を「並び替え」と捉える。まず 1 が正しい位置に来るように, 1 ともう一つ元を選んで1回(または0回)互換する。次に 2 が正しい位置に来るように, 2 ともう一つ元を選んで1回(または0回)互換する。この操作を続ければよい。
略証終
なお実際の分解の仕方は一通りではなく,複数通りあります。ただし,偶数個の互換の積になるか,奇数個の互換の積になるかは常に一定です。これは,互換 \tau に対して,
\prod_{i<j} (\tau(j) - \tau(i)) = - \prod_{i<j} (j-i)
となることと,元の置換 \sigma に対し,
の符号はすでに決定していることから従います。
奇置換・偶置換と置換の符号
奇置換・偶置換の定義
定義(奇置換・偶置換)
奇数個の互換の積で書ける置換を奇置換 (odd permutation) と言い,偶数個の互換の積で書ける置換を偶置換 (even permutation) という。
なお,
\prod_{i<j} (\sigma(j) - \sigma(i))
が負のとき奇置換,正のとき偶置換と定義しても同じになります。これは,直前で述べたことから従います。
置換の符号の定義
定義(置換の符号)
\sigma が奇置換のとき,\color{red} \operatorname{sgn} \sigma = -1 ,偶置換のとき \color{red}\operatorname{sgn} \sigma = 1 と定義し,これを置換の符号 (sign, signature) という。
さて,この符号が行列式の定義において必要になってきます。「数字の並び替え」が奇数回なら符号は -1 となり,偶数回なら 1 となると覚えましょう。
このとき,以下は知っておくべきでしょう。
定理(置換と置換の符号)
- \color{red}\operatorname{sgn}(\tau\sigma)=(\operatorname{sgn}\tau)(\operatorname{sgn}\sigma).
- \color{red}\operatorname{sgn}\sigma = \operatorname{sgn}\sigma^{-1} .
1.は,実際に奇置換か偶置換かで 2\times 2=4 通りの場合分けを行うことで分かります。
2.は,互換を「入れ替え」とみると,逆置換はその「逆再生」であり,入れ替え回数は変わらないことから従います。
行列式(det)
今回は,線形代数学とくに行列における行列式に必要な知識のみに絞って解説しました。これで,行列式の定義は理解できるでしょう。行列式については,以下を参照してください。