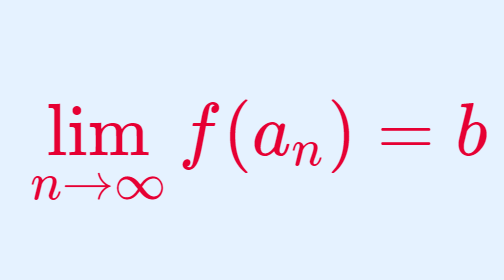実数上の関数において，「関数の収束 \iff 数列の収束」という定理を紹介します。微分積分学において，関数の収束と数列の収束を結びつける重要な定理ですから，しっかりと理解しましょう。
関数の収束⇔数列の収束
定理（関数の収束 \iff 数列の収束）
f \colon \mathbb{R} \to \mathbb{R}, \,\, a\in \mathbb{R} とする。このとき，
- \displaystyle \lim_{x\to a} f(x) = b
\iff
\displaystyle a_n \ne a, \lim_{n\to\infty} a_n = a となる任意の数列 \{a_n\} に対して，\displaystyle \lim_{n\to\infty} f(a_n) = b - \displaystyle \lim_{x\to a} f(x) 収束する
\iff
\displaystyle a_n \ne a, \lim_{n\to\infty} a_n = a となる任意の数列 \{a_n\} に対して，\displaystyle \lim_{n\to\infty} f(a_n) が収束する
1.と2.の違いは，収束する値を定めているか，単に収束すると言っているだけなのかの違いです。特に2.では，この主張だけを見ると「数列の取り方によって収束する値は変わってもよい」というように見えます（実際はそんなことはなく，同じ値に収束することを今から証明します）。
なお， f \colon \mathbb{R} \to \mathbb{R} としましたが，定義域は a の周りだけで構いません。また，より一般に f\colon \mathbb{R}^m \to \mathbb{R}^n や \mathbb{C} でも同様に成立します。
関数の収束⇔数列の収束の証明
証明には，数列の極限・関数の極限の両方を理解しておかねばなりません。これについて分からない場合は，まず以下の2記事を参照してください。
これをある程度分かった上で，2つの証明を見ていきましょう。
証明
1. \displaystyle \lim_{x\to a} f(x) = b
\iff
\displaystyle a_n \ne a, \lim_{n\to\infty} a_n = a となる任意の数列 \{a_n \} に対して，\displaystyle \lim_{n\to\infty} f(a_n) = b
\implies について
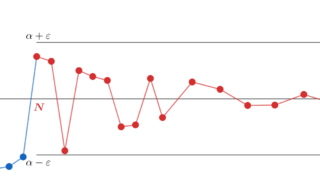
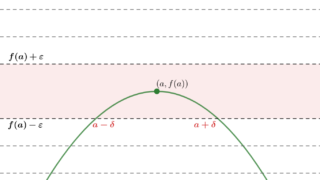
\varepsilon > 0 とする。すると，ある \delta > 0 が存在して，
0 < |x-a| < \delta \implies |f(x) - b| < \varepsilon
が成立する。このとき a_n \ne a, \lim_{n\to\infty} a_n = a となる数列を取ると，その定義から，ある N \ge 1 が存在して，
とできる。これはすなわち，
を意味し， \lim_{n\to\infty} f(a_n) = b である。
\impliedby について
対偶を示すことにする。 \lim_{x\to a} f(x) = b が成立しないとする。すると，ある \varepsilon > 0 が存在して，任意の \delta > 0 に対して，
0 < |x- a| < \delta \quad\text{and}\quad |f(x) - b| \ge \varepsilon
をみたす x が存在する。これより \delta = 1/n として， n 毎に
となる a_n が取れる。この \{a_n \} は， a_n \ne a, a_n \xrightarrow{n\to\infty} a をみたすが，常に | f(a_n) - b| \ge \varepsilon が成立するため， f(a_n) は b に収束しない。よって対偶が示せた。
2. \displaystyle \lim_{x\to a} f(x) 収束する
\iff\displaystyle a_n \ne a, \lim_{n\to\infty} a_n = a となる任意の数列 \{a_n\} に対して，\displaystyle \lim_{n\to\infty} f(a_n) が収束する
\implies について
1.より明らか。
\impliedby について
主張中の任意の \{a_n\} が同じ値に収束することが分かれば，1.が適用できて証明が終わる。よってこれを証明しよう。
背理法で示す。 \{a_n\} , \{a_n^\prime\} で，\displaystyle a_n , a_n^\prime \ne a,\,\, \lim_{n\to\infty} a_n , \lim_{n\to\infty} a_n^\prime = a だが，\displaystyle b = \lim_{n\to\infty} f(a_n) \ne \lim_{n\to\infty} f(a_n^\prime) = b^\prime としよう。このとき，
a^{\prime\prime}_{2n-1} = a_n, \quad a^{\prime\prime}_{2n} = a^\prime_n
として新たな数列 \{ a^{\prime\prime}_n \} を作ると，これは \displaystyle a^{\prime\prime}_n \ne a, \lim_{n\to\infty} a^{\prime\prime}_n = a を満たしているが， f(a^{\prime\prime}_n) は収束しない ( b\ne b^\prime の「両方に近づく」)。よって仮定に矛盾。
証明終
何とか証明できましたね。お疲れさまでした。
