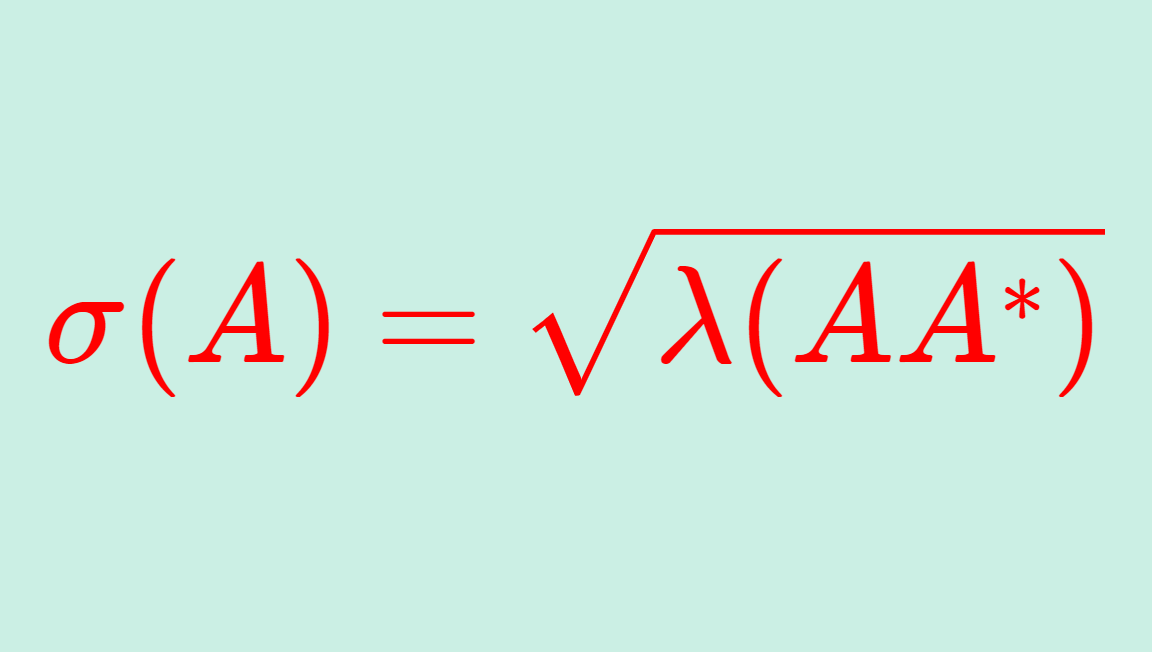行列の特異値とは,一般の m\times n 行列に対して定義される固有値みたいなものです。厳密には, AA^* のように正方行列にしてから,固有値を考えます。
行列の特異値について,定義と性質を述べましょう。
行列の特異値とは
正方行列(m\times m 行列)のみに定義される固有値は,行列の「本質的な性質を取り出すもの」であり,行列やそれに関連する分野のさまざまな計算において大切なものです。
m\times n 行列に対しても,似たようなことを考えたい。定義を述べましょう。
定義(特異値)
A を m\times n 行列, A^*=\overline{A}^\top をその随伴行列(共役転置)とする。このとき, AA^* は m 次正方行列であるが,その固有値 \lambda(AA^*) の平方根
\large \color{red} \sigma(A)=\sqrt{\lambda(AA^*)}
を A の特異値 (singular value) という。
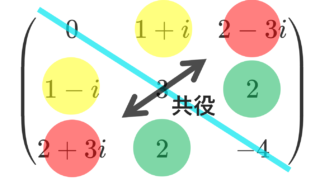
AA^* はグラム行列とよばれ,半正定値エルミート行列です。特に, A が実行列のときは,半正定値対称行列となります。
半正定値エルミート行列は,全ての固有値が非負の実数であることが知られています(→正定値行列・半正定値行列の定義・性質3つとその証明)。従って, AA^* の固有値の平方根をとっても非負の実数なので, A の特異値は非負の実数になります。
これ以外の性質を述べましょう。
特異値の性質
定理(特異値の性質)
A を m\times n 行列とする。
\sigma_i(A) を A の上から数えて 0\le i\le m 番目に大きな特異値とし,\lambda_i(AA^*) を, AA^* の上から数えて 1\le i\le m 番目に大きな固有値とする。このとき, 1\le i\le \min\{ m,n\} に対して,
- \sigma_i(A)=\sqrt{\lambda_i(AA^*)}=\sqrt{\lambda_i(A^*A)}
- \sigma_i(A)=\sigma_i(A^*)
\sigma_i(A)=\sqrt{\lambda_i(AA^*)} はただの定義ですね。それ以外を示しましょう。
証明
1. \sqrt{\lambda_i(AA^*)}=\sqrt{\lambda_i(A^*A)} について
A を m\times n 行列とする。1\le i\le \min\{m,n\} に対し, \lambda_i(AA^*)=\lambda_i(A^*A) を示せばよい。
定義の直後で述べたように, AA^*, A^*A の固有値は非負の実数である。
AA^* の固有値を大きい順に \lambda_1\ge \lambda_2\ge \dots \ge \lambda_m\ge 0 とし,対応する固有ベクトルを \boldsymbol{x_1},\boldsymbol{x_2},\dots, \boldsymbol{x_m} とする。固有ベクトルは一次独立であることに注意する。特に, \lambda_k>0,\,\lambda_{k+1}=\dots =\lambda_m=0 としてよい。 1\le i\le m に対し,
\begin{aligned}(A^*A)A^*\boldsymbol{x_i}&= A^*(AA^*)\boldsymbol{x_i}\\&=A^*(\lambda_i \boldsymbol{x_i})\\&=\lambda_iA^*\boldsymbol{x_i}\end{aligned}
である。\lambda_i\ne 0 のとき,上式より A^*\boldsymbol{x_i}\ne\boldsymbol{0} である。よって, i\le k に対し, \lambda_i は A^*A の固有値であり, A^*\boldsymbol{x_i} はその固有ベクトルである。
A と A^* の役割を入れ替えて同様に考えることで,
\boldsymbol{\lambda\ne 0} が \boldsymbol{AA^*} の固有値 \boldsymbol{ \iff \lambda\ne 0} が \boldsymbol{A^*A} の固有値
となることが分かる。
AA^*\boldsymbol{x_1}=\boldsymbol{x_1},\dots, AA^*\boldsymbol{x_k}=\boldsymbol{x_k} は一次独立であるから, A^*\boldsymbol{x_1},\dots, A^*\boldsymbol{x_k} も一次独立である。よって, AA^*, A^*A の 0 でない固有値は,重複度を含めて一致する。
以上から, AA^* の上から数えて i 番目に大きい固有値は, A^*A の上から数えて i 番目に大きい固有値に一致する。
2. \sigma_i(A)=\sigma_i(A^*) について
\begin{aligned}\sigma_i(A)&=\sqrt{\lambda_i(AA^*)}\\ \sigma_i(A^*)&= \sqrt{\lambda_i(A^*A)} \end{aligned}
であり,1.より \lambda_i(AA^*)=\lambda_i(A^*A) なので,結論を得る。
証明終
1. の議論は,より一般に AB と BA の固有値の話に一般化できます( AB,BA の両方の積が定義できる場合に限る)。