 群・環・体
群・環・体 直交群・回転群(特殊直交群)とは~定義と性質~
直交群・回転群(特殊直交群)とは,それぞれ直交行列・回転行列の集合のなす群を言います。これについて,定義と性質を述べましょう。
 群・環・体
群・環・体  線形代数学
線形代数学  数論
数論 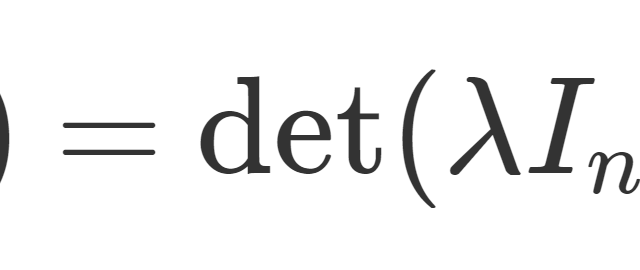 線形代数学
線形代数学 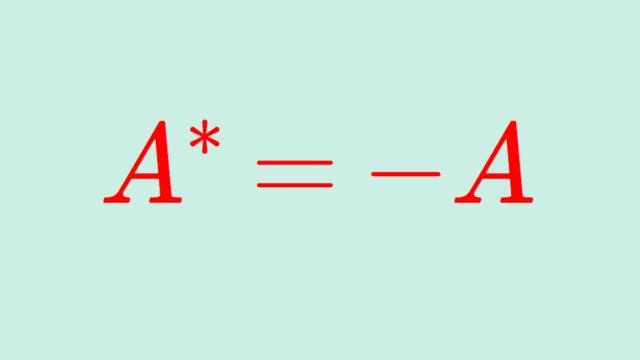 線形代数学
線形代数学  線形代数学
線形代数学 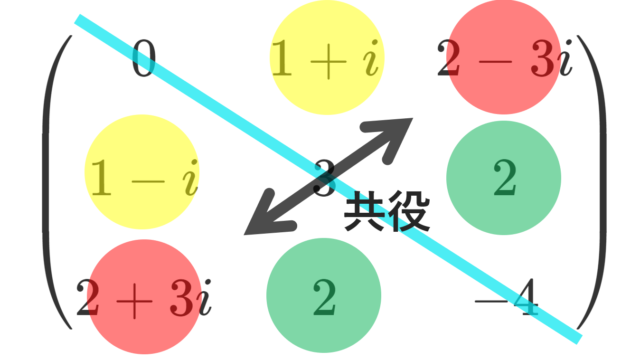 線形代数学
線形代数学 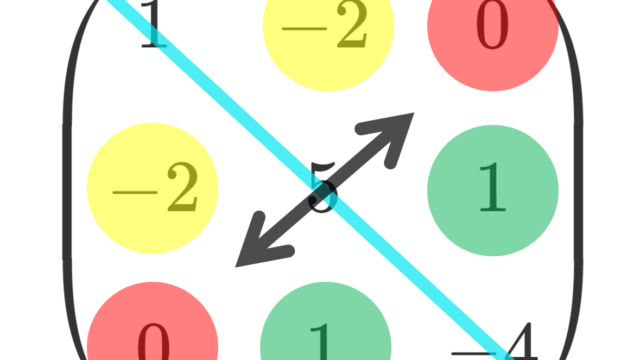 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学