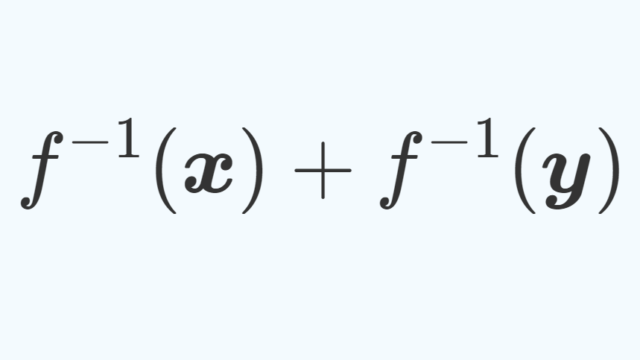 線形代数学
線形代数学 線形同型写像とベクトル空間の同型
線形同型写像とは,全単射な線形写像を指します。このような写像が存在する2つのベクトル空間は同型であるといい,全く同じものとして扱うことが可能です。線形同型写像とベクトル空間の同型について,基本的なことをおさえましょう。
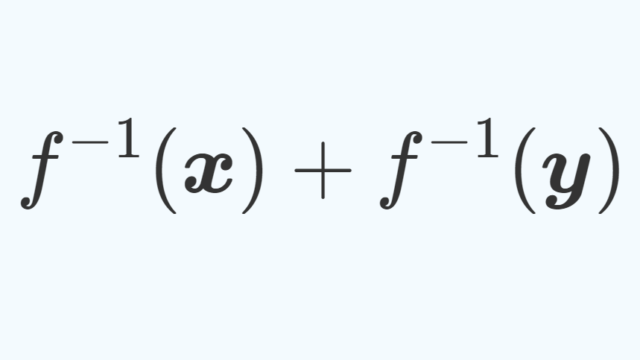 線形代数学
線形代数学 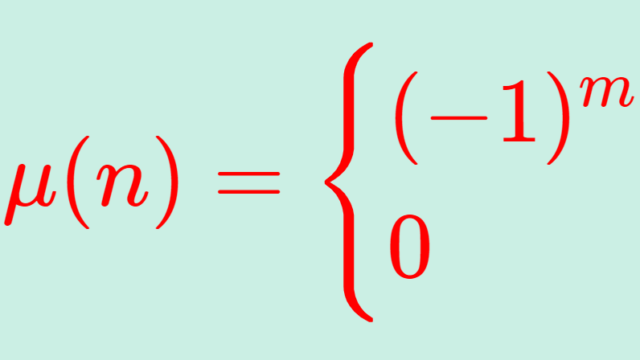 数論
数論 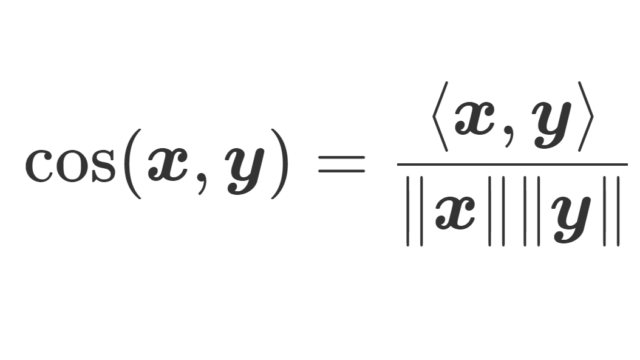 統計学
統計学 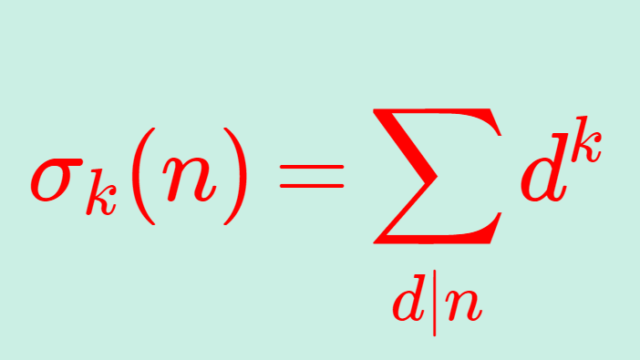 数論
数論 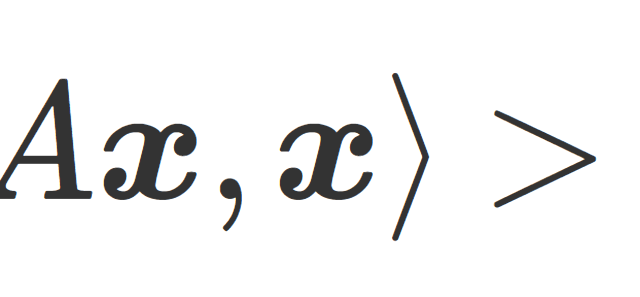 線形代数学
線形代数学 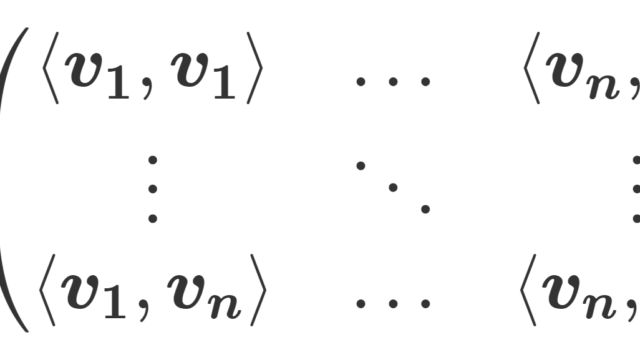 線形代数学
線形代数学 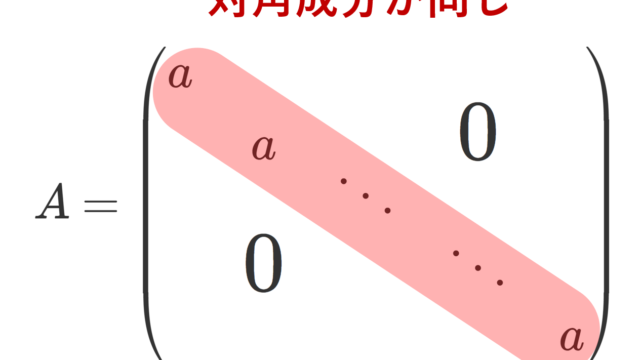 線形代数学
線形代数学 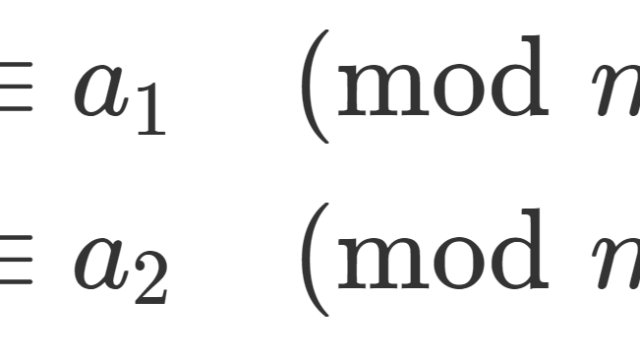 数論
数論 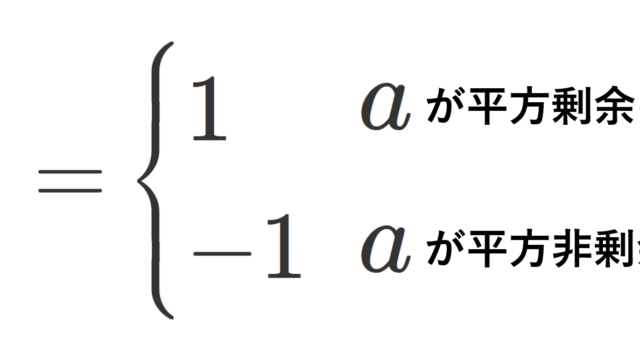 数論
数論 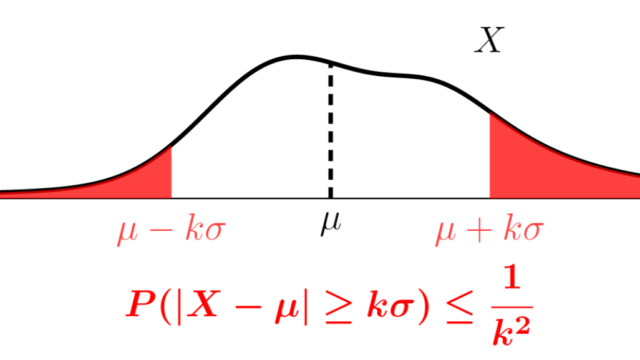 確率論
確率論