 統計学
統計学 ベイズの定理をわかりやすく簡潔に
ベイズの定理 (Bayes' theorem) とは,条件付き確率に関する等式を指します。これについて,その証明と,意義も含めた応用例を紹介しましょう。
 統計学
統計学 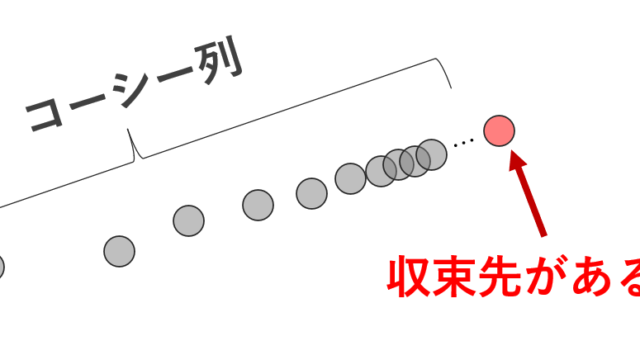 集合と位相
集合と位相 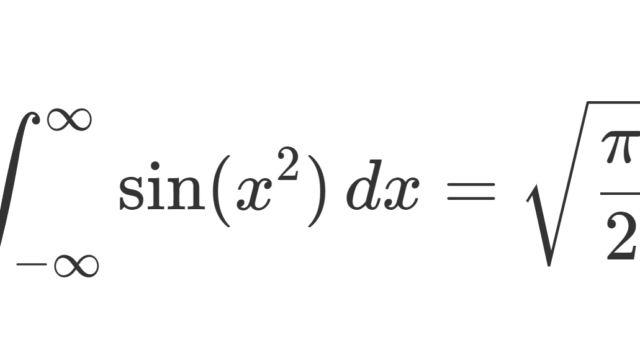 複素関数論
複素関数論 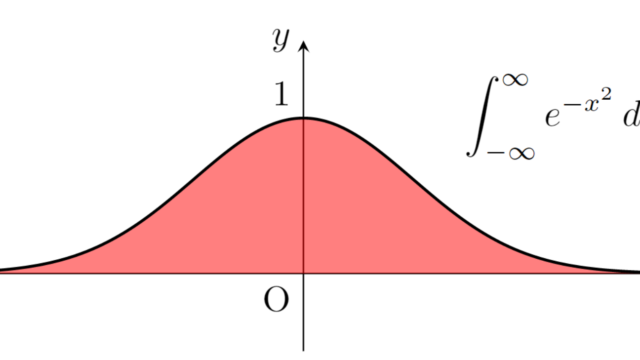 微分積分学(大学)
微分積分学(大学) 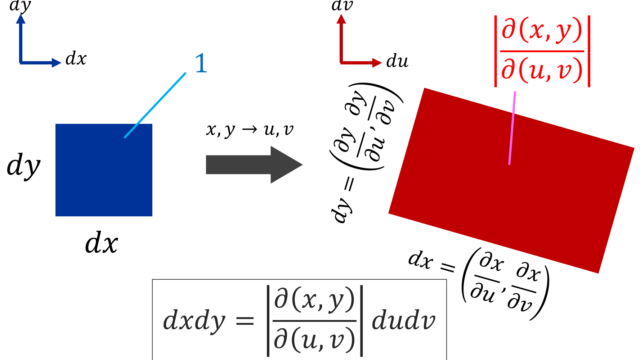 微分積分学(大学)
微分積分学(大学) 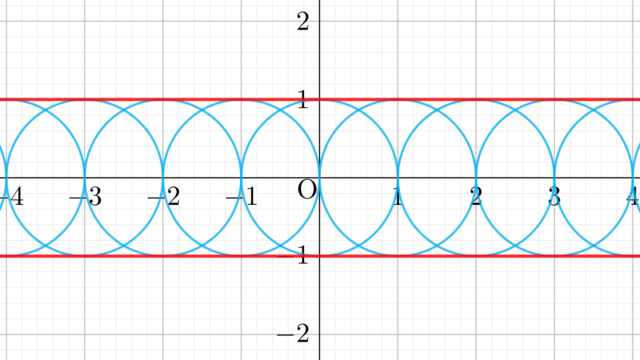 微分積分学(大学)
微分積分学(大学) 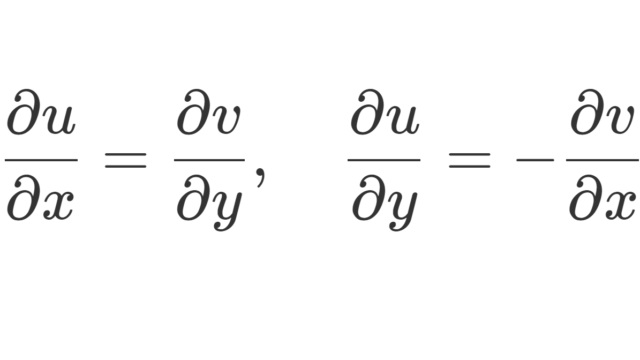 複素関数論
複素関数論 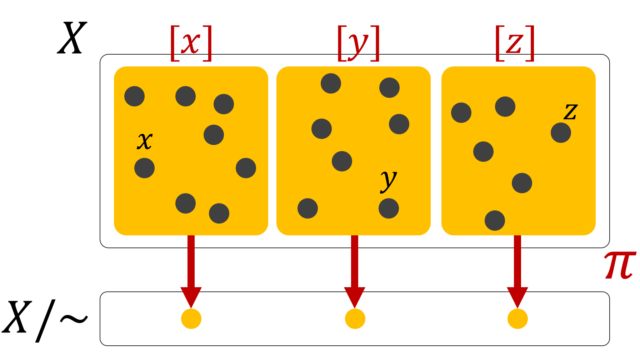 集合と位相
集合と位相  集合と位相
集合と位相 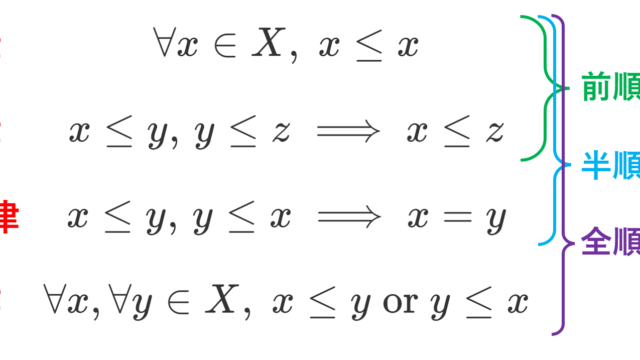 集合と位相
集合と位相