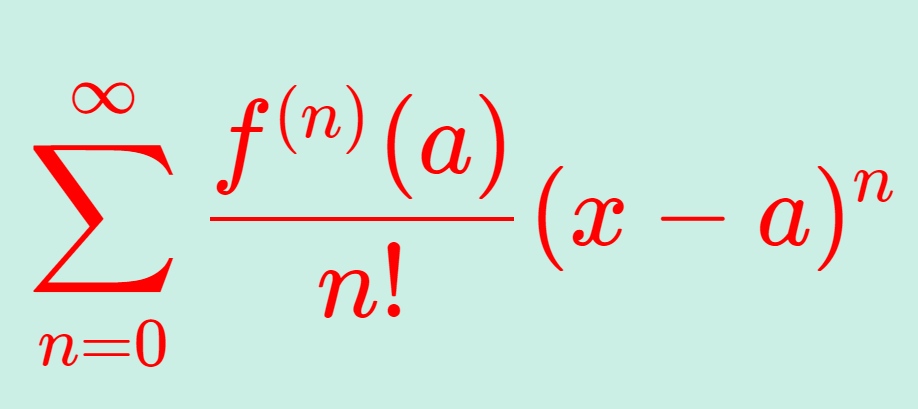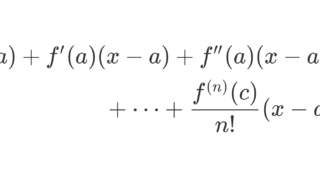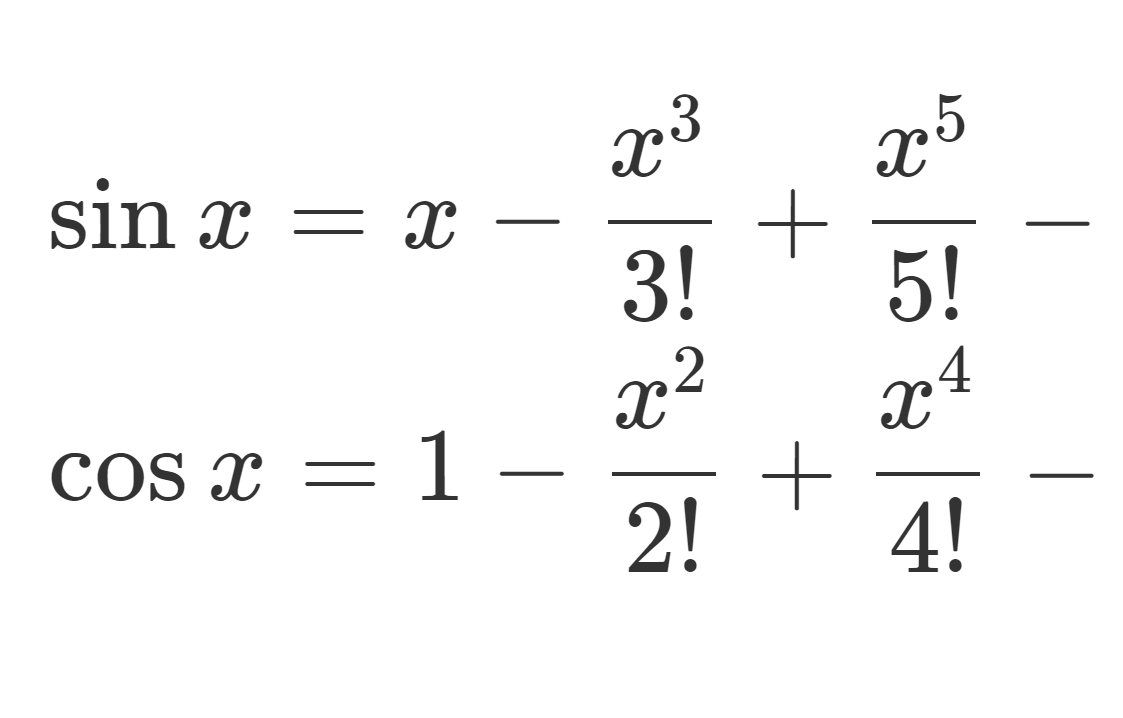大学の微分積分学で習うテイラー展開（テーラー展開）・マクローリン展開は，関数のべき級数展開と言えます。まずはその定義とその感覚的な理解，そして具体例を述べます。そして無限回微分可能であっても，マクローリン展開できないような関数が存在するため，そうした例にも触れましょう。
テイラー展開・マクローリン展開の定義と解析的な関数
まずはテイラー展開・解析的な関数とマクローリン展開の定義をざっくりと述べ，それからテイラーの定理・マクローリンの定理を用いてもう一度述べることにします。
テイラー展開・解析的な関数の定義
定義（テイラー展開・解析的な関数）
f を C^\infty 級関数とする(すなわち無限回微分可能な関数)。 f が a の近くで
\color{red}\begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(a)}{n!} (x-a)^n \\ &= f(a) + f'(a)(x-a) + \frac{f''(a)}{2!} (x-a)^2 + \\ &\qquad + \frac{f'''(a)}{3!} (x-a)^3 +\frac{f''''(a)}{4!} (x-a)^4 + \cdots \end{aligned}
とできるとき，これを f の a の周りのテイラー展開（テーラー展開; Taylor expansion) といい，この級数をテイラー級数 (Taylor series) という。
定義域全ての点 a において，その十分近くでテイラー展開可能な関数を解析的 (analytic) であるという。
C^\infty 級関数の言葉の意味についてはC1級,Cn級,C∞級関数の定義と具体例5つを参照してください。
注意ですが， C^\infty 級であればどんな関数でもテイラー展開できるというわけではありません。これについては，後ほど詳しく述べます。
定義の右辺は， x についてのべき級数になっていますから，テイラー展開とは a の近くでのべき級数展開であると言えますね。
なお，ここでいう a の十分近くの「十分近く」がどれだけの範囲になるかは，関数によって変わります。
マクローリン展開の定義
テイラー展開において， a=0 としたもの，すなわち 0 の周りでのべき級数展開を考えたものがマクローリン展開です。定義を述べましょう。
定義（マクローリン展開）
f を C^\infty 級関数とする(すなわち無限回微分可能な関数)。 f が 0 の近くで
\color{red}\begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(0)}{n!} x^n \\ &= f(0) + f'(0)x + \frac{f''(0)}{2!} x^2 \\ &\qquad +\frac{f'''(0)}{3!} x^3 + \frac{f''''(0)}{4!} x^4+ \cdots \end{aligned}
とできるとき，これを f のマクローリン展開 (Maclaurin expansion) といい，この級数をマクローリン級数 (Maclaurin series) という。
マクローリン展開はテイラー展開で a =0 とした，特別な場合と言えますね。
テイラーの定理・マクローリンの定理からテイラー展開・マクローリン展開へ
上でテイラー展開・マクローリン展開の定義をざっくりと述べました。これは，いわゆる「 n 次までのべき級数展開」であるテイラーの定理・マクローリンの定理を用いて書き直すことができます。テイラーの定理・マクローリンの定理とは以下のようなものです。
f は a の近くで n 回微分可能であるとする。このとき，
\small \color{red} \begin{aligned} f(x) ={}&\sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x-a)^k + \frac{f^{(n)}(c)}{n!}(x-a)^n \\ ={}& f(a)+ f'(a)(x-a) + \frac{ f''(a)}{2!}(x-a)^2 \\ &\hspace{50pt}+ \dots+ \frac{f^{(n)}(c)}{n!}(x-a)^n \end{aligned}
となる a<c<x が存在する。ここで，最終項 \color{red} R_n = \dfrac{f^{(n)}(c)}{n!}(x-a)^n をラグランジュの剰余項という。
テイラーの定理で a=0 としたものがマクローリンの定理です。
f は 0 の近くで n 回微分可能であるとする。このとき，
\small\color{red} \begin{aligned} f(x) ={}&\sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} x^k + \frac{f^{(n)}(c)}{n!}x^n \\ ={}& f(0)+ f'(0)x +\frac{ f''(0)}{2!}x^2 \\ & \hspace{50pt} + \dots + \frac{f^{(n)}(c)}{n!}x^n \end{aligned}
となる 0<c<x が存在する。ここで，最終項 \color{red} R_n = \dfrac{f^{(n)}(c)}{n!}x^n をラグランジュの剰余項という。
テイラーの定理・マクローリンの定理の証明については，以下の記事を参照してください。
テイラーの定理・マクローリンの定理の重要な点は，剰余項部分 R_n がある点 c \in [a,x] を用いて書けるというところなんですが，今回重要なのはそこではありません。単に R_n \xrightarrow{n\to\infty} 0 となることが大切です。
このことを踏まえると，テイラー展開・マクローリン展開の定義は次のようになります。
定義（テイラー展開・解析的な関数）
f を C^\infty 級関数とする。 f が a の近くでのテイラーの定理の剰余項について R_n \xrightarrow{n\to\infty} 0 となるならば，
\color{red}\begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(a)}{n!} (x-a)^n \\ &= f(a) + f'(a)(x-a) + \frac{f''(a)}{2!} (x-a)^2 + \\ &\qquad + \frac{f'''(a)}{3!} (x-a)^3 +\frac{f''''(a)}{4!} (x-a)^4 + \cdots \end{aligned}
とできる。これを f の a の周りのテイラー展開（テーラー展開; Taylor expansion) という。
定義域全ての点 a において，その十分近くでテイラー展開可能な関数を解析的 (analytic) であるという。
定義（マクローリン展開）
f を C^\infty 級関数とする。 f における， 0 の近くでのマクローリンの定理の剰余項について， R_n \xrightarrow{n\to\infty} 0 となるならば，
\color{red}\begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(0)}{n!} x^n \\ &= f(0) + f'(0)x + \frac{f''(0)}{2!} x^2 \\ &\qquad +\frac{f'''(0)}{3!} x^3 + \frac{f''''(0)}{4!} x^4+ \cdots \end{aligned}
とできる。これを f のマクローリン展開 (Maclaurin expansion) という。
なおここで， x, や a は実数でも複素数でも構いません。複素数にしたときは，級数部分の微分は複素数の意味になります。
テイラー展開・マクローリン展開の感覚的な理解
感覚的な理解，すなわち「お気持ち」を少しだけ述べることにしましょう。
もし，関数 f(x) が多項式，すなわち f(x) = a_0 + a_1 x + \dots+ a_n x^n の形であったとします。このときの a_k の値はどうやれば求まるでしょうか。
その方法の一つが，微分を用いることです。実際，以下のように値が求まります。
\begin{aligned} a_0 &= f(0), \\ a_1 &= f'(0), \\ a_2 &= \frac{f''(0)}{2!}, \\ \cdots \\ a_n& = \frac{f^{(n)}(0)}{n!}. \end{aligned}
このことから f(x) が多項式なら
と表せるのが分かるでしょう。ところで，微分するだけであれば，無限回微分可能な関数なら一般に計算できますよね。よって，多項式でない関数だったとしても，同じような変形は可能です。
要するに，マクローリン展開とは f(x) 多項式だと思って「その多項式を求めている」とみることができます。テイラー展開も同じですが，式を a だけ平行移動したものになります。
これがテイラー展開・マクローリン展開の感覚的な理解です。
マクローリン展開の具体例
テイラー展開で特に x=a としたマクローリン展開について，主な関数の例を挙げてみましょう。
マクローリン展開の具体例
- \small \displaystyle e^x = 1+ x + \frac{x^2}{2!} + \dots + \frac{x^n}{n!} + \cdots, \,\, (|x|<\infty).
- \small \displaystyle \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dots + (-1)^n \frac{x^{2n+1}}{(2n+1)!} + \cdots, \,\, (|x|<\infty).
- \small \displaystyle \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots + (-1)^n \frac{x^{2n}}{(2n)!} + \cdots, \,\, (|x|<\infty).
- \small \displaystyle \log(1+ x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \dots + (-1)^{n-1} \frac{x^{n}}{n} + \cdots, \,\, (-1<x\le 1).
- \small \displaystyle (1+x)^\alpha = 1 + \alpha x + \frac{\alpha(\alpha-1)}{2!}x^2 + \dots + \frac{\alpha(\alpha-1)\dots(\alpha-n+1)}{n!}x^n + \cdots,\, (-1 < x \le 1).
ここで，マクローリン展開は 0 の近くでの展開の訳ですが，それがどの範囲かというのが括弧の中に示したものです。
たとえば e^x であれば実数全体で等式が成立することになります。
これは収束半径といわれるものと密接に関連していますが，収束半径と求め方については【べき級数】収束半径の定義と求め方とその具体例3つで解説しています。
\sin, \cos のマクローリン展開については，三角関数sin,cosのマクローリン展開(0でのテイラー展開)も参照してください。 \log(1+x) のマクローリン展開については，log(1+x)の0でのテイラー展開(マクローリン展開)も参照してください。
C^∞級だが解析的でない(テイラー展開できない)例
テイラー展開を述べた際に， C^\infty 級であればどんな関数でもテイラー展開できるというわけではありません。と述べました。ここでは，そうした「テイラー展開できない」関数の典型例を挙げましょう。
C^\infty 級だが解析的でない関数の例
\color{red}f(x) = \begin{cases} e^{-1/x} & x> 0, \\ 0 & x \le 0 \end{cases} は C^\infty 級であるが，マクローリン展開(原点の周りでテイラー展開)できない。
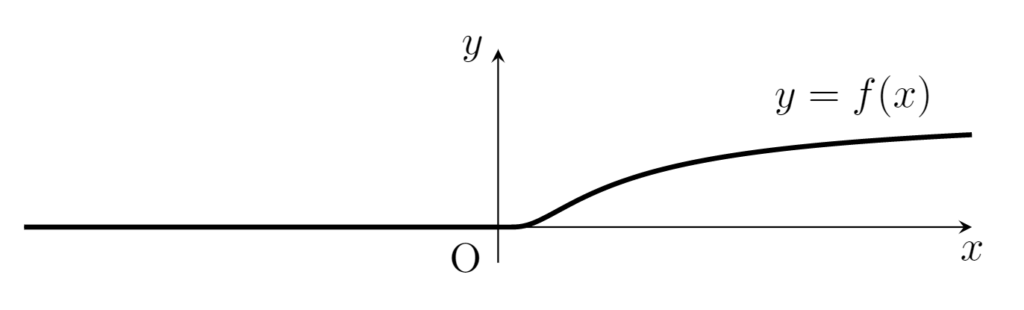
実際，この関数は C^\infty 級ですが， f^{(n)}(0) = 0 \,\, (n\ge 0 ) なので，マクローリン展開しようと思うと
\sum_{n=0}^\infty\frac{ f^{(n)}(0)}{n!} x^n = 0
になりなす。しかし，これは 0 のまわり，特に(十分小さい) x>0 で f(x) に一致してないことが分かりますね。
このように， C^\infty 級でも解析的であるとは限らないので，注意が必要です。
複素関数では1回微分可能ならば解析的
実関数 f\colon \mathbb{R} \to \mathbb{R} においては， C^n 級であっても C^{n+1} 級とは限りませんし， C^\infty 級であっても解析的であるとは限りませんでした。(cf. C1級,Cn級,C∞級関数の定義と具体例5つ)
しかし，複素関数 \color{red} f\colon \mathbb{C} \to \mathbb{C} においては，複素数の意味で 1 回微分可能ならば無限回微分可能であり，しかも解析的であるということが分かっています。定理の主張のみ述べておきましょう。
定理（複素関数の正則性）
複素関数 f\colon \mathbb{C} \to \mathbb{C} が(複素数の範囲で)微分可能ならば解析的である。
このとき，この関数は正則 (regular analytic) であるという。
複素数は，実数よりもかなり性質が良いということが分かります。
おわりに
テイラー展開は，解析学における大事な概念の1つです。「 C^\infty 級関数」と「解析的な関数」の違いも含めて，しっかりと理解しておくようにしましょう。
