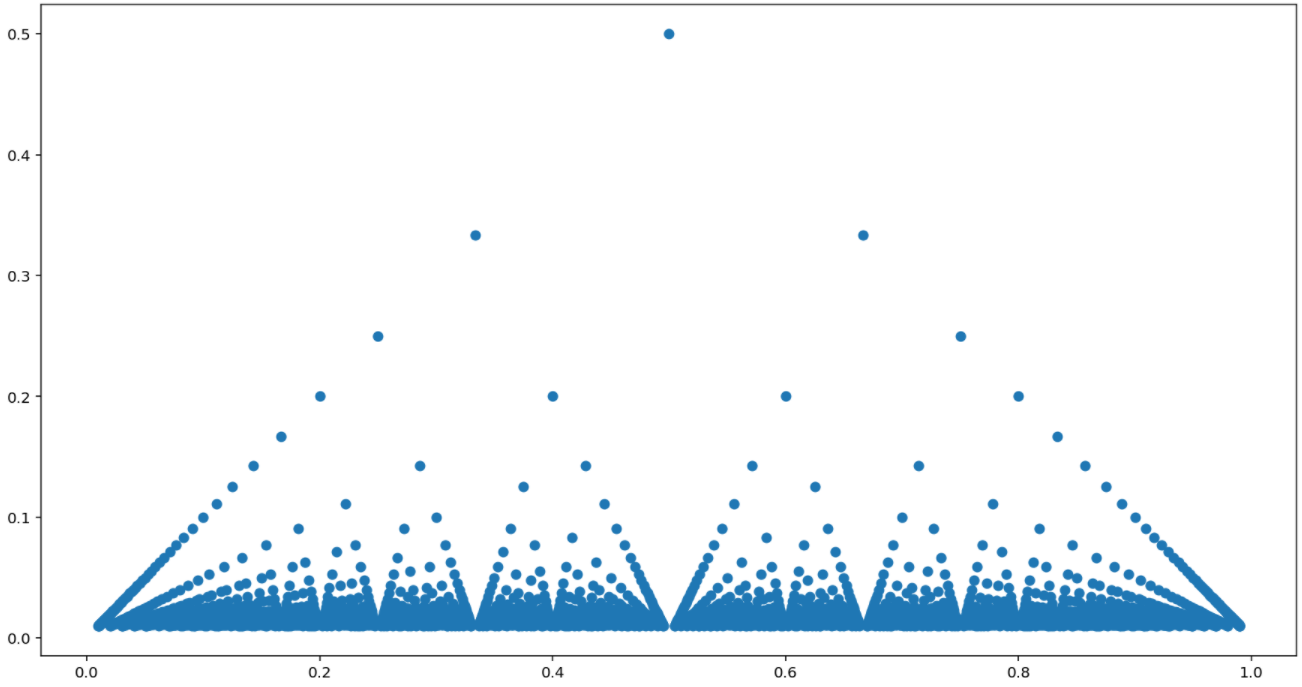
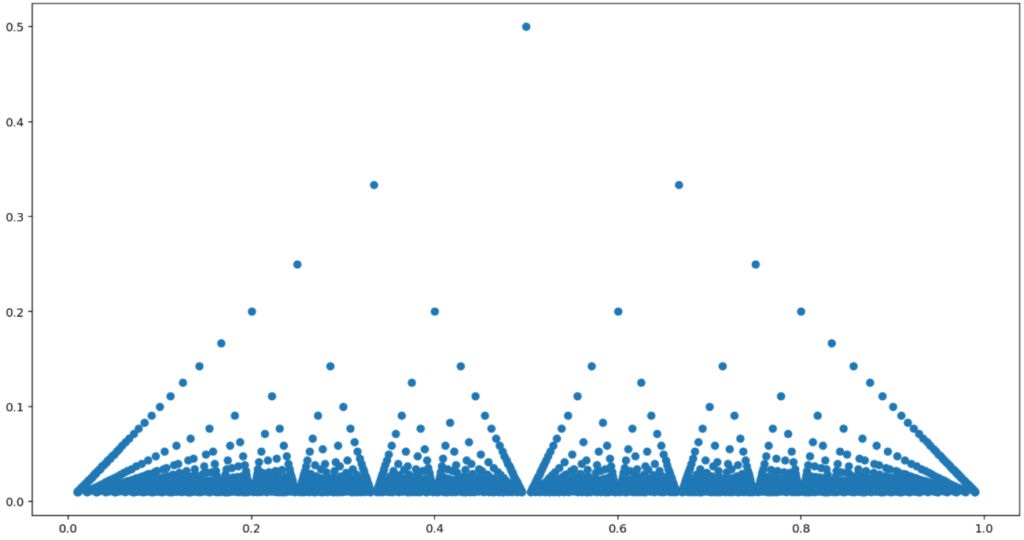
有理数で分母分の 1，無理数で 0 である関数をトマエ関数と言います。この関数について，その定義と性質2つを紹介しましょう。
トマエ関数の定義
さっそく，トマエ関数を定義しましょう。
定義（トマエ関数）
\color{red} f(x) = \begin{dcases} \frac{1}{p} & x = \frac{q}{p} \;\; (p\ge 0, \, \operatorname{gcd}(p,q)=1), \\ 0 & x \in \mathbb{R}\setminus\mathbb{Q} \end{dcases}
をトマエ関数 (Thomae’s function) という。（厳密には \color{red} f(0)=1 とする）
有理数上では，その数を互いに素に表示したときの分母によって関数の値が決まり，無理数では単に 0 になる関数ですね。
図で描くと，以下のようになります。
トマエ関数の性質
トマエ関数の性質について，
- 無理数で連続，有理数で不連続
- リーマン積分可能
であることを紹介しましょう。
トマエ関数は無理数で連続，有理数で不連続
トマエ関数の最も有名な性質としては，連続性でしょう。
定理（トマエ関数の連続性）
トマエ関数は無理数上で連続であるが，有理数上では不連続な関数である。
連続点と不連続点がともに稠密に存在しているような関数というわけですね。
証明
有理数上では不連続であることについて
x \in \mathbb{Q} とする。このとき， f(x) > 0 である。 \{r_n\} \subset \mathbb{R} \setminus \mathbb{Q} を無理数列とし， r_n \xrightarrow{n\to\infty} x としよう。このとき， f(r_n)=0 であるから，
\lim_{n\to\infty} f(r_n) = 0 \ne f(x) .
従って， f は x で連続でない。
無理数上では連続であることについて
x \in \mathbb{R}\setminus\mathbb{Q} とする。また， \varepsilon>0 とする。このとき， N\ge 1 が存在して， 1/N < \varepsilon とできる。
\delta = \min_{\substack{1\le n \le N\\ k \in \mathbb{Z}}}\left| x-\frac{k}{n}\right|
としよう。このとき， |x-y| < \delta をみたす任意の y に対して， f(y) \le 1/N である。よって，
なので， f は x で連続である。
証明終
トマエ関数はリーマン積分可能
トマエ関数は，積分することが可能です。これについても紹介しましょう。
証明
\varepsilon > 0 に対して， 1/N < \varepsilon となる整数 N \ge 1 をとる。
区間の分割 a=x_0 < x_1 < \dots < x_n =b を分割の幅 |\varDelta| = \max_{1\le k \le n} |x_{k}-x_{k-1}| が |\varDelta|< \varepsilon/N^2 とすると， t_k \in [t_{k-1}, t_k ] を代表元としたときのリーマン和
\sum_{k=1}^n f(t_k) (x_k-x_{k-1})
について， 1/N \le f(t_k) \le 1 となるのは高々 N^2 個であるから，そうなる区間と，残りの f(t_k) \le 1/N となる区間に分けて和を考えることで，
が分かる。これより， |\varDelta| \to 0 とすると，リーマン和は 0 に収束する。従って，トマエ関数はリーマン積分可能で，その値は 0 である。
証明終
