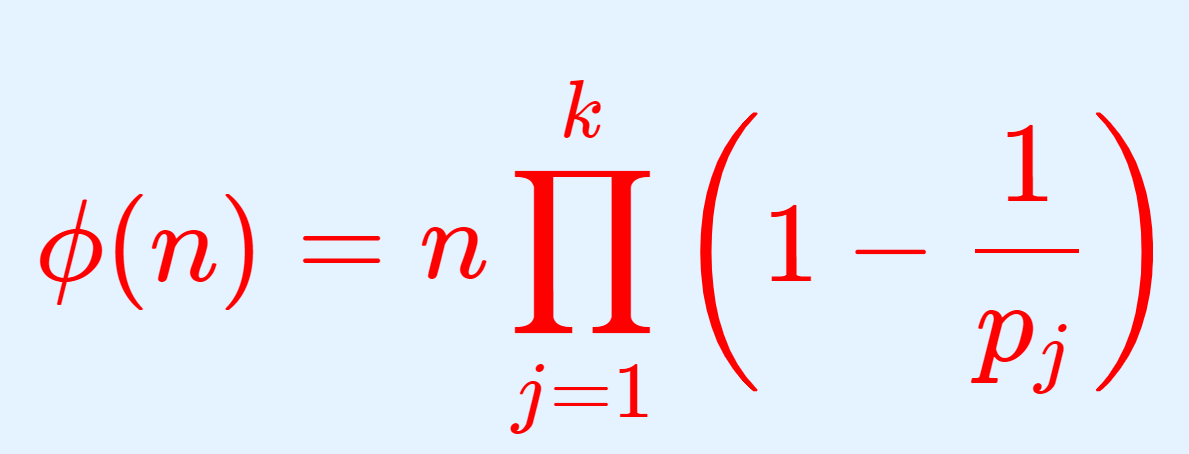二項演算・単項演算は,厳密には集合上の写像として定義されます。これについて,その定義と例を紹介しましょう。
二項演算・単項演算とは
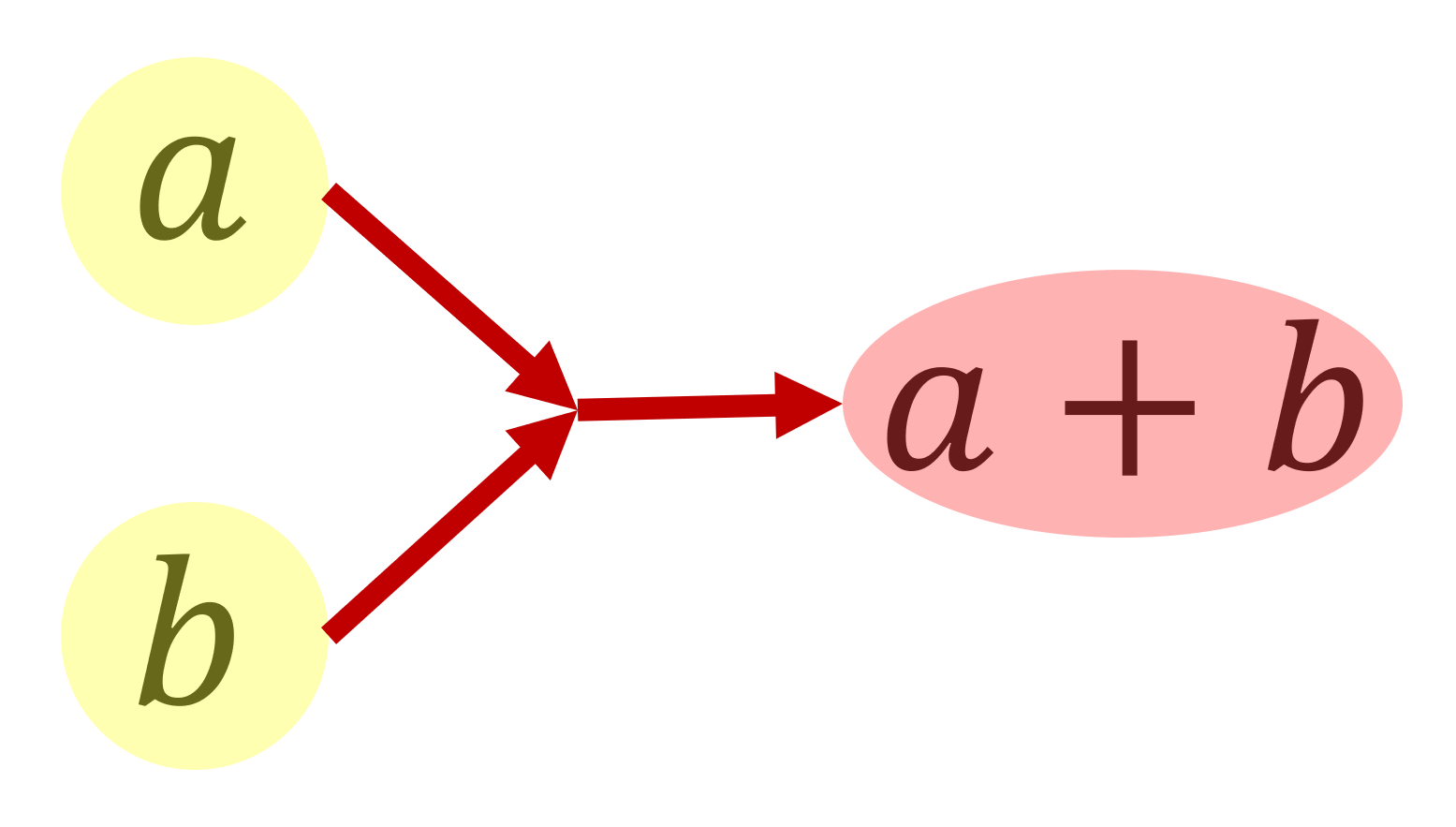
二項演算とは, a,b に対し,a+b を作るような演算を指します。これは何かというと,集合の中から2つ元を取ってきて,それを組み合わせて別の元を作る操作ですね。
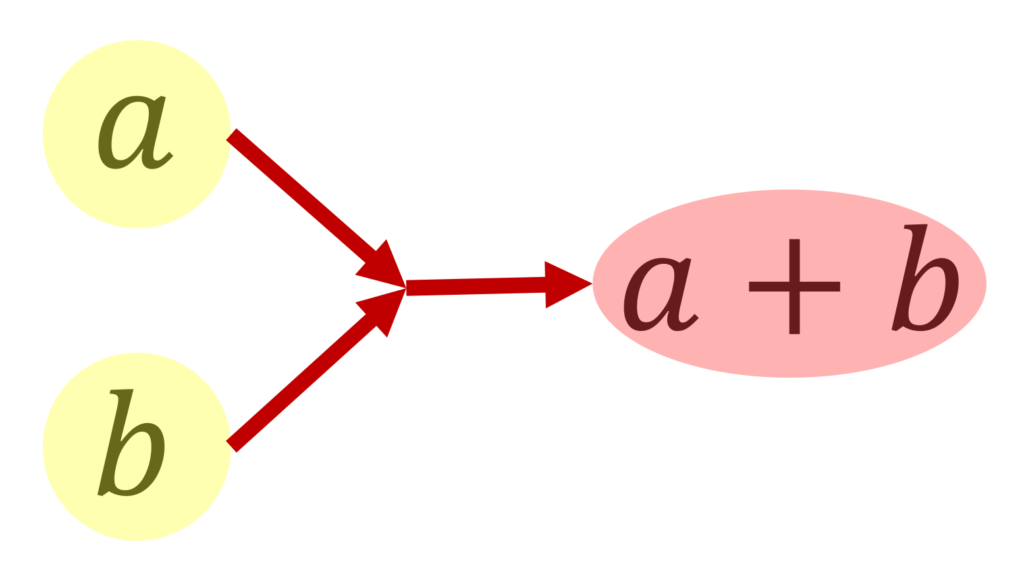
これは,直積集合 A\times A から A への写像と言えますね。
単項演算とは, a に対し, -a を作るような演算を指します。これは何かというと,集合の中から1つ元を取ってきて,それから別の元を作る操作ですね。
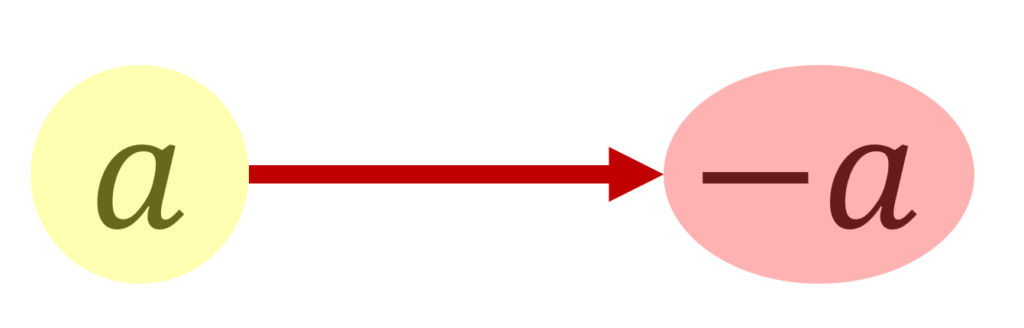
これは,A から A への写像と言えますね。
ちゃんとした定義をまとめましょう。
定義(二項演算・単項演算)
A を空でない集合とする。
\phi が A 上の二項演算 (binary operation) であるとは,写像 \color{red}\phi \colon A\times A \to A のことをいう。
\psi が A 上の単項演算 (unary operation) であるとは,写像 \color{red} \psi\colon A\to A のことをいう。
「演算」とは写像だと考えられるわけですね。例をまとめましょう。
二項演算・単項演算の例
二項演算の例1(数の和).
\mathbb{R} 上の和の演算 \mathbb{R}\times \mathbb{R}\ni (a,b)\mapsto a+b \in\mathbb{R} は二項演算である。
例にも述べた,和の演算です。
二項演算の例2(数の積).
\mathbb{R} 上の積の演算 \mathbb{R}\times \mathbb{R}\ni (a,b)\mapsto ab \in\mathbb{R} は二項演算である。
積についても同様ですね。
単項演算の例1(正負の変換).
\mathbb{R} 上の正負の変換の演算 \mathbb{R}\ni a \mapsto -a \in\mathbb{R} は単項演算である。
正負を変える操作です。上の画像で例にも述べたとおりですね。
単項演算の例2(インクリメント).
\mathbb{Z} 上の 1 加える演算 \mathbb{Z}\ni a \mapsto a+1 \in\mathbb{Z} は単項演算である。
プログラミングだと a++; が上と同じことを意味することが多いでしょう。これを「インクリメント」ということがあります。これも単項演算の一種ですね。
もう少し別の例を紹介しましょう。
二項演算・単項演算の例3.
\mathcal{F} を \emptyset \in\mathcal{F} かつ
\begin{aligned}A,B\in\mathcal{F}&\implies A\cup B\in\mathcal{F}, \\ A\in\mathcal{F} &\implies A^c\in\mathcal{F} \end{aligned}
をみたす集合族とする。このとき, (A,B)\mapsto A\cup B は二項演算で, A\mapsto A^c は単項演算である。
上のような \mathcal{F} を有限加法族 (finitely additive class) といいます(→σ加法族と可測空間の定義・基本的な性質をわかりやすく)。