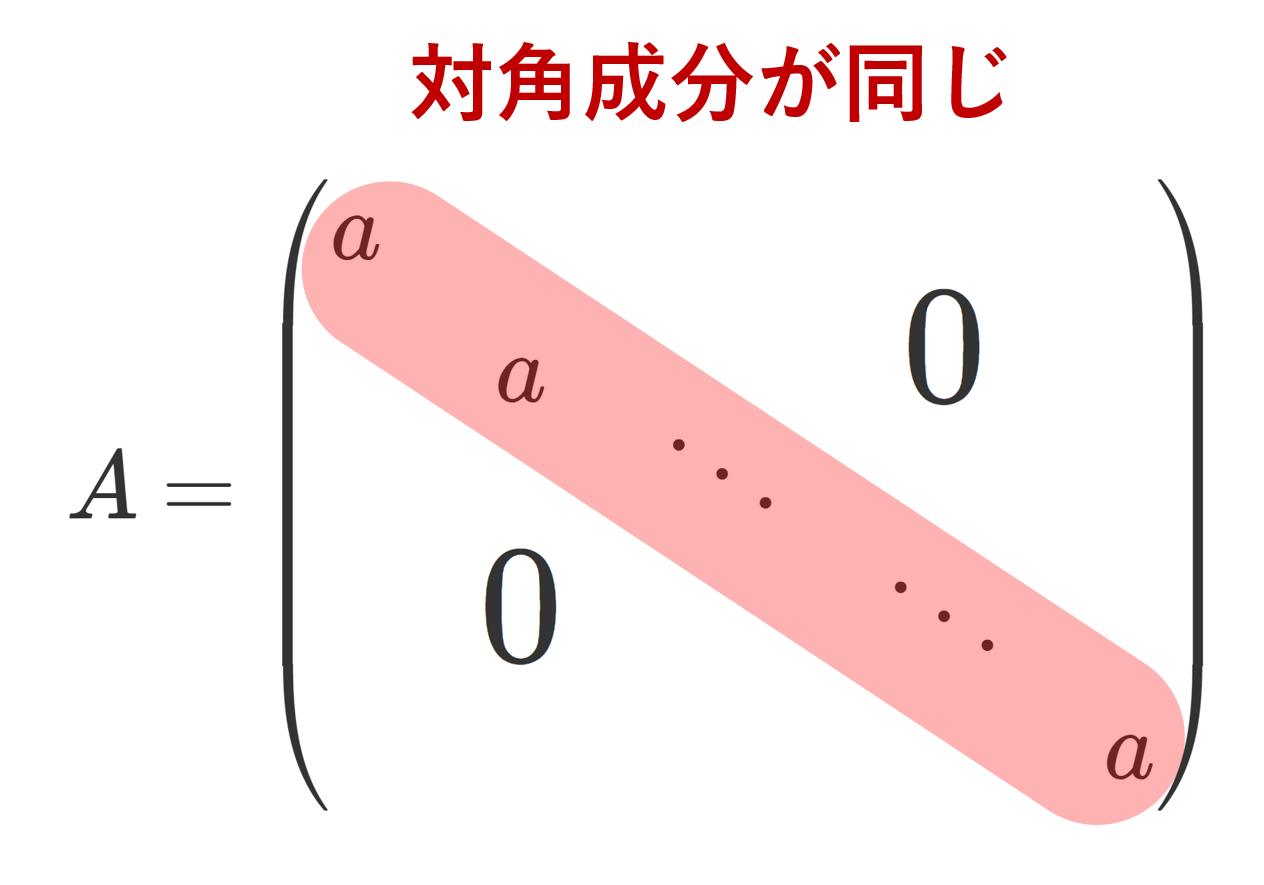
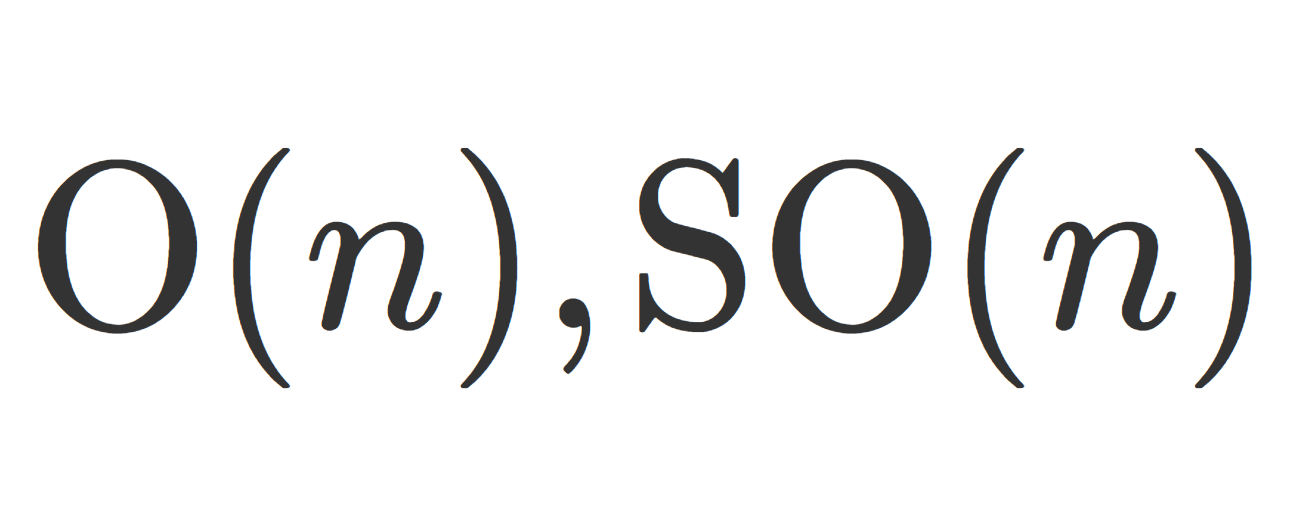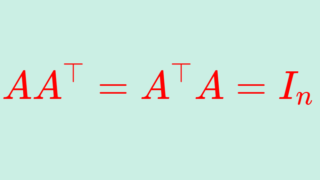直交群・回転群(特殊直交群)とは,それぞれ直交行列・回転行列の集合のなす群を言います。これについて,定義と性質を述べましょう。
直交群・回転群(特殊直交群)の定義
直交群の定義
以下, \mathrm{GL}_n(\mathbb{R}) を,各成分を実数とする n 次正則行列(可逆行列)全体の集合とします。
定義(直交群)
n 次正方行列に関する集合
\color{red}\mathrm{O}(n) = \{ A\in \mathrm{GL}_n(\mathbb{R})\mid AA^\top =A^\top A=I_n\}
は行列の積に関して群となる。これを直交群 (orthogonal group) という。 I_n は n 次単位行列である。
AA^\top = A^\top A=I_n は言い換えると A^{-1} = A^\top ですね。このような A を直交行列 (orthogonal matrix) といいます。直交行列で大事なのは以下の性質です。
A,B を直交行列とするとき,
- 単位行列 I_n も直交行列である。
- AB も直交行列である。
- A^{-1} も直交行列である。
- \det A = \pm 1 .
1.は自明ですね。2,3,4.は,以下で証明しています。
\mathrm{GL}_n(\mathbb{R}) も積に関して群なので, \mathrm{O}(n) は \mathrm{GL}_n(\mathbb{R}) の部分群になります。上の「直交群の大事な性質1-3.から」,\mathrm{O}(n) が部分群になることは分かりますね(→部分群の定義と判定方法~例4つと性質~)。
回転群(特殊直交群)の定義
定義(回転群(特殊直交群))
直交群 \mathrm{O}(n) の部分集合
\color{red}\mathrm{SO}(n) = \{ A\in \mathrm{O}(n)\mid \det A = 1\}
は行列の積に関して部分群となる。これを回転群 (特殊直交群; rotation group) という。
直交群の元は \det A = \pm 1 でしたが,回転群は \det A=1 のみを考えた部分群なわけですね。 \det は行列式の意味です(→行列式(det)の定義と現実的な求め方~計算の手順~)。部分群であることは明らかでしょう。
直交群・回転群(特殊直交群)の性質
定理(直交群・回転群(特殊直交群)の性質)
- \mathrm{SO}(n) は \mathrm{O}(n) の正規部分群である。また, \mathrm{O}(n)/\mathrm{SO}(n)\simeq \{\pm 1\} となる。
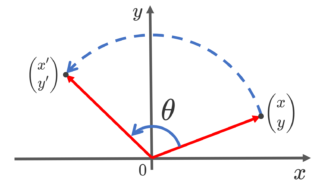
- \mathrm{SO}(2) = \{R_\theta\mid \theta\in\mathbb{R}\}. ただし, R_\theta =\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} は回転行列である。
2.で出てくる回転行列は, R_{\alpha+\beta}=R_\alpha R_\beta,\; R_\theta^{-1} = R_{-\theta} をみたします。以下で解説しています。
定理を証明していきましょう。
1. SO(n)はO(n)の正規部分群であり,O(n)/SO(n)={±1}であること
証明
A\in \mathrm{O}(n),\; S\in \mathrm{SO}(n) とする。このとき,
\begin{aligned}\det (ASA^{-1}) &= \det A \det S \det A^{-1}\\ &= \det S =1 \end{aligned}
なので, ASA^{-1}\in \mathrm{SO}(n) である。したがって, \mathrm{SO}(n) は正規部分群である。また,
は全射準同型であり, \operatorname{Ker} f = \mathrm{SO}(n) である。よって準同型定理より, \mathrm{O}(n)/\mathrm{SO}(n) \simeq \{\pm 1\} である。
証明終
一般に群準同型 f に対し, \operatorname{Ker} f は正規部分群であることが知られています(→正規部分群の定義と基本的な判定方法・具体例)から,前半の証明はなくても構いません。
2. SO(2)は回転行列を群と見たものであること
証明
S = \begin{pmatrix} a& b\\ c& d \end{pmatrix}\in\mathrm{SO}(2) とする。
SS^\top =\begin{pmatrix} a^2+b^2 & ac+bd \\ ac+bd & c^2+d^2\end{pmatrix} = I_2
なので, a^2+b^2=c^2+d^2=1,\, ac+bd=0 である。
a^2+b^2=c^2+d^2=1 より, a=\cos\theta, \, b=-\sin\theta ,\, c=\sin\varphi, \, d = \cos\varphi となる \theta,\varphi \in \mathbb{R} が存在する。
ac+bd=0 より,加法定理から \sin(\theta-\varphi)=0 なので, \theta -\varphi \equiv 0, \pi \pmod{2\pi} である。
\det S =1 より, ad-bc=1 なので,加法定理から \cos(\theta-\varphi)=1 となる。よって, \theta-\varphi \equiv 0 \pmod{2\pi} である。
以上から, \varphi \equiv \theta \pmod{2\pi} なので, c=\sin\theta,\, d=\cos\theta となって結論を得る。
証明終
回転群という名前は,回転行列とも密接に関係しています。