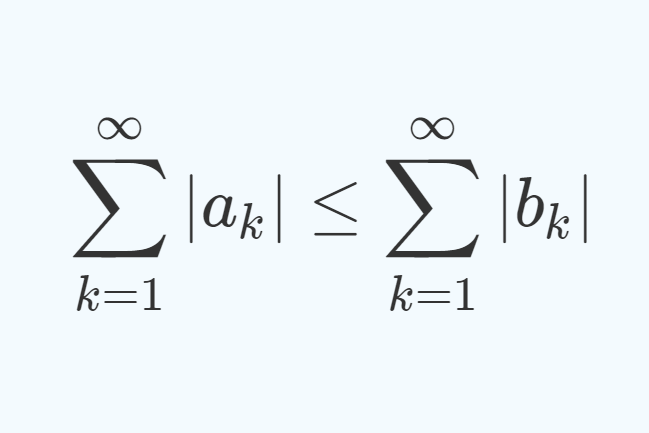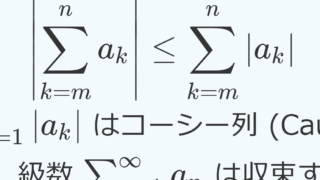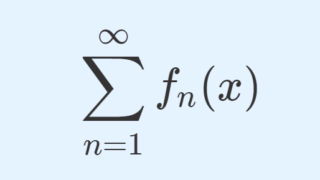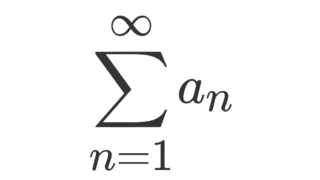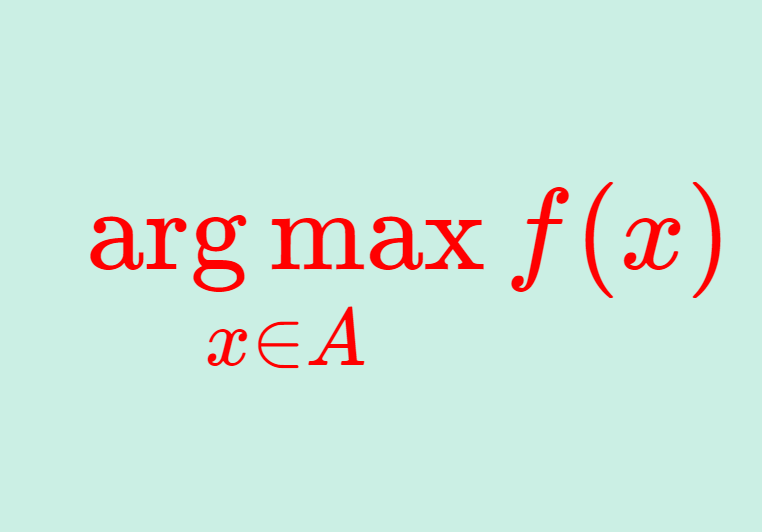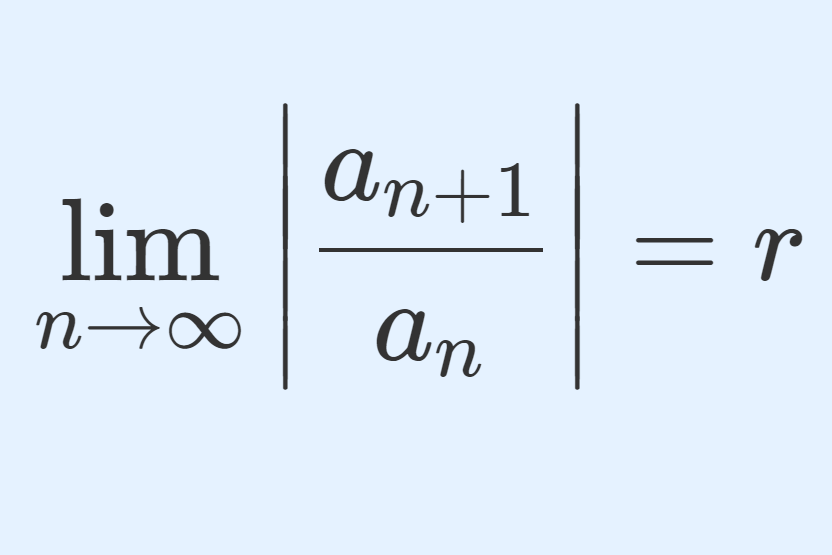【級数の収束】比較判定法は最も基本的かつ有用なものである

級数 $\sum_{n=1}^\infty a_n$ の収束・発散の議論にあたって，比較判定法は最も基本的かつ有用なものです。これについて紹介します。

級数の収束の比較判定法
比較判定法の証明と補足
1. 比較判定法の証明
2. 比較判定法の補足
比較判定法の具体例
ワイエルシュトラスのM判定法
その他の収束判定法

級数の収束の比較判定法

定理（比較判定法; comparison test, 優級数定理; dominated series theorem）

数列 $\{a_n\}, \{b_n\}$ に対し， $|a_n| \le |b_n|$ かつ $\sum_{n=1}^\infty |b_n| < \infty$ ならば，

\sum_{n=1}^\infty |a_n| < \infty

も成立する。すなわち， $\sum_{n=1}^\infty a_n$ は絶対収束する。

級数の収束判定法は他にもさまざまなものが知られていますが，それらが確かに使えることの証明は，基本的にこの比較判定法を無意識的に用いて行われます。
その他の場面でも無意識的に使われることが多いですね。

ここでいう「無意識」とは，証明が簡単なのでわざわざ「比較判定法より」と言わないという意味です。

比較判定法の証明と補足

比較判定法の証明

証明は簡単と思うかもしれませんが，きちんと確認しておきましょう。

証明

$|a_n| \le |b_n|$ より，

\sum_{k=1}^n |a_k| \le \sum_{k=1}^n |b_k|

である。両辺 $n\to\infty$ として，

\sum_{k=1}^\infty |a_k| \le \sum_{k=1}^\infty |b_k|

が成立し，とくに $\sum_{k=1}^\infty |a_k| < \infty$ である。

証明終

比較判定法の補足

補足ですが，絶対収束すなわち $\sum_{n=1}^\infty |a_n| < \infty$ であれば，元の級数 $\sum_{n=1}^\infty a_n$ も有限値に収束することが有名です。これについては以下を参照してください。

比較判定法の具体例

いくつか具体例を挙げて，その有用性を確認しましょう。

例1.

$\displaystyle \textcolor{red}{\sum_{n=1}^\infty \frac{1}{2^n n} }$ は絶対収束する。

実際， $\displaystyle \frac{1}{2^n n} \le \frac{1}{2^n }$ かつ $\displaystyle \sum_{n=1}^\infty \frac{1}{2^n} = 1 < \infty$ より，比較判定法から絶対収束します。

例2.

$\displaystyle \textcolor{red}{\sum_{n=1}^\infty \frac{\sin n\pi/6}{2^n} }$ は絶対収束する。

実際， $\displaystyle \left| \frac{\sin n\pi/6}{2^n} \right| \le \frac{1}{2^n }$ かつ $\displaystyle \sum_{n=1}^\infty \frac{1}{2^n} = 1 < \infty$ より，比較判定法から絶対収束します。

例3.

$\displaystyle \textcolor{red}{\sum_{n=1}^\infty \frac{1}{n^2} }$ は絶対収束する。

実際， $\displaystyle \frac{1}{n^2} \le \begin{cases} \frac{1}{n(n-1) } = \frac{1}{n-1} - \frac{1}{n} & n \ge 2, \\ 1 & n =1 \end{cases}$ かつ $\displaystyle \sum_{n=2}^\infty \left(\frac{1}{n-1} - \frac{1}{n} \right) = \lim_{n\to\infty} \left(1 - \frac{1}{n}\right) = 1 < \infty$ より，比較判定法から絶対収束します。

なお， $\sum_{n=1}^\infty 1/n^\alpha \,\, (\alpha > 0)$ の収束・発散については積分による収束判定法も有名です。これについては，以下を参照してください。