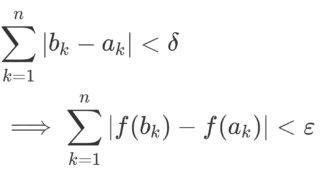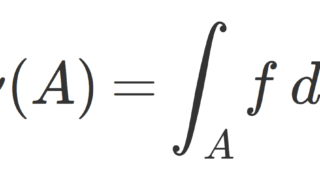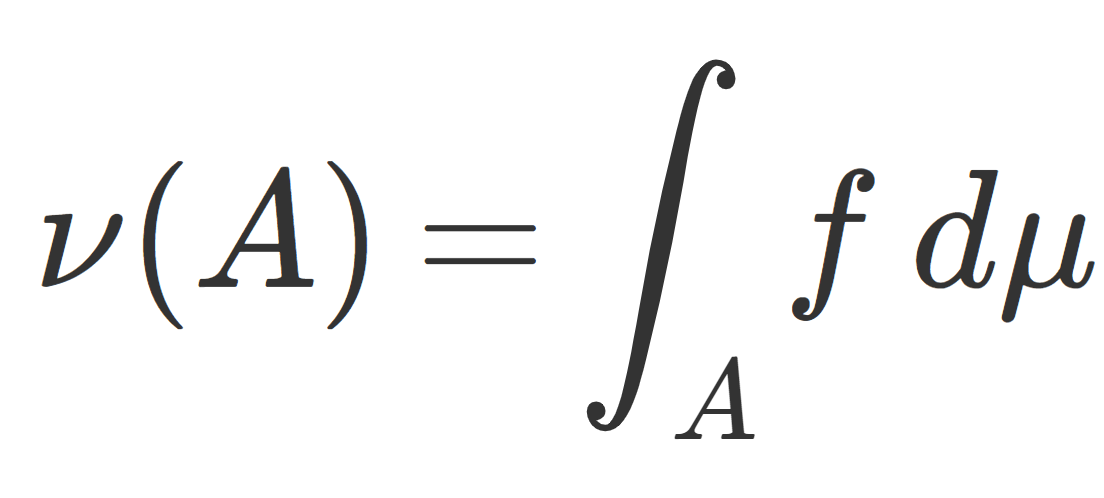同じ可測空間に測度が二つあるときに,その二つの測度の関係性を述べるのが測度の絶対連続性・同値性・特異性です。
また任意のσ有限な測度は,別の測度に関して絶対連続なものと特異なものの和に分解できることが知られており,これをルベーグの分解定理といいます。
測度の絶対連続性・同値性・特異性と,ルベーグの分解定理について,証明付きで紹介しましょう。
測度の絶対連続性・同値性・特異性
定義(絶対連続性・同値性・特異性)
(X,\mathcal{F}) を可測空間とし, \mu,\nu をその上の測度とする。
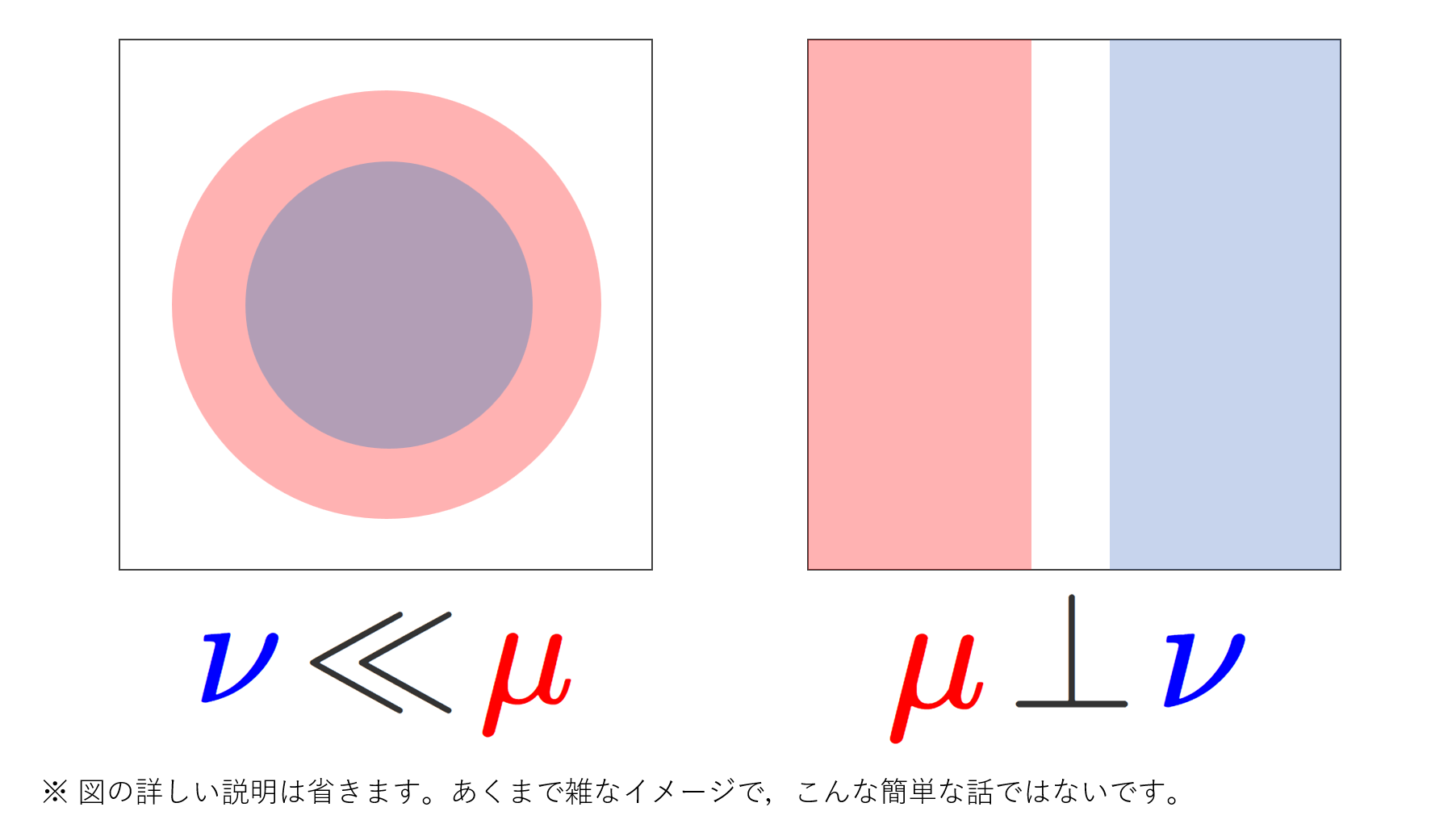
\nu が \mu に関して絶対連続 (absolutely continuous) であるとは,
\mu(A)=0, \; A\in\mathcal{F}\implies \nu(A)=0
が成り立つことを言う。これを \color{red}\large \nu\ll \mu とかく。\mu,\nu がともに測度であり,\nu\ll \mu かつ \mu\ll \nu が成り立つとき,測度 \mu,\nu は同値 (equivalent) であるという。
\mu と \nu が互いに特異 (singular) であるとは,ある A\in\mathcal{F} が存在して,
\mu(A)=\nu(A^c)=0
が成り立つことを言う。これを \color{red}\large \mu\perp\nu とかく。
同値な測度の場合「大きさ」を持っている集合は同じであり,逆に特異な測度の場合,「大きさ」を持っている集合は全く異なるということですね。「測度が同値である」という関係は,同値関係になっています。

\nu\ll \mu と \nu\perp\mu が同時に成立するならば,\nu は零測度です。実際,特異性から \mu(A)=\nu(A^c)=0 とすると,絶対連続性より \nu(A)=\mu(A)=0 もわかるため, \nu(X)=0 になります。
また,\mu,\nu が符号付き測度のときは,|\mu|,|\nu| に対して同様に絶対連続性や同値性・特異性を定義します。
ルベーグの分解定理
ルベーグの分解定理 (Lebesgue decomposition theorem)
(X,\mathcal{F}) を可測空間とし, \mu,\nu をその上のσ有限な測度とする。このとき,
\large\color{red}\begin{gathered}\nu=\nu_c+\nu_s, \\ \nu_c \ll \mu,\quad \nu_s\perp \mu \end{gathered}
のように,\nu を \mu に関して絶対連続な測度 \nu_a と特異な測度 \nu_s の和に分解でき,この分解は一意的である。
\nu=\nu_c+\nu_s を \mu に関する \nu のルベーグ分解 (Lebesgue decomposition) といいます。
なお,σ有限の仮定は非常に重要です。たとえば, \R 上のルベーグ測度を m,数え上げ測度を \# としましょう。このとき, \# を定理のように m に関して分解することはできません。実際,もし \#= \#_c+\#_s と分解できたとすると, A が有限集合のとき, \#_c(A)=m(A)=0 でなければなりませんから,結局 \#=\#_s となります。しかし, \#(A)=0\iff A=\emptyset のため, \#=\#_s が m と特異になるためには, \#(\emptyset)=m(\R)=0 でなければなりませんが,これはおかしいですね。
証明
まず \nu が有限測度の場合に示す。
\alpha =\sup_{N\in\mathcal{F} , \; \mu(N)=0} \nu(N)
とすると,supの定義より,ある \{N_n\}\subset \mathcal{F} が存在して,\mu(N_n)=0 かつ \lim_{n\to\infty} \nu(N_n)=\alpha とできる。ここで, N=\bigcup_{n=1}^\infty N_n とすると,
1つ目から \mu(N)=0 であり,これと \alpha の定義から \nu(N)\le \alpha となる。また,2つ目の式で n\to\infty とすることで \nu(N)\ge \alpha も従うため,結局 \nu(N)=\alpha である。 A\in\mathcal{F} に対し,
と定義する。このとき,明らかに \nu=\nu_c+\nu_s である。また, \mu(N)=\nu_s(N^c)=0 より,\nu_s\perp \mu である。 \nu_c\ll \mu を示そう。これが成り立たないと仮定すると,ある S\in\mathcal{F} が存在して, \mu(S)=0 かつ \nu_c(S)>0 が成立することになるが,このとき, \mu(N\cup S)=0,\; \nu(N\cup S)=\nu(N)+\nu_c(S)>\alpha となって, \alpha の定義に矛盾している。よって \nu_c\ll \mu である。
一意性について示す。\nu_c+\nu_s=\nu'_c+\nu'_s をともにルベーグ分解とすると, \nu_c-\nu'_c=\nu'_s-\nu_s であり,左辺が \mu に関して絶対連続な符号付き測度で,右辺が \mu と特異な符号付き測度であることが示せる。したがって,両辺 \mu に関して絶対連続かつ \mu と特異であるから,零測度である(理由は定義の後に述べた)。よって \nu_c=\nu'_c,\; \nu_s=\nu'_s であり,一意性が示された。
次に \nu がσ有限のとき
全体空間 X を,どの二つも互いに素で, \nu(X_n)<\infty をみたすような空間 \{X_n\} に分割して考えればよい。
証明終
ルベーグ測度に関するルベーグの分解定理
\mu をルベーグ測度としたときには,もう少し細かく分解することが普通です。
ルベーグ測度に関するルベーグの分解定理
可測空間 (\R,\mathcal{B}(\R)) 上のルベーグ測度を m とする。このとき,この上の任意のσ有限測度 \nu は,
\large \color{red}\nu=\nu_{\mathrm{dis}}+\nu_{\mathrm{cont}}+\nu_{\mathrm{sing}}
の形に一意的に分解できる。ただし,
- \nu_{\mathrm{dis}} は離散測度
- \nu_{\mathrm{cont}} は m に関して絶対連続な測度
- \nu_{\mathrm{sing}} は特異連続測度
である。
離散測度 (discrete measure) とは, c_n>0 と x に大きさを持つデルタ測度 \delta_x を用いて, \nu_{\mathrm{dis}}=\sum_{n=1}^\infty c_n \delta_{x_n} の形でかける測度のことです。離散測度は明らかにルベーグの測度と特異です。 \nu_{\mathrm{dis}}(\R\setminus\{ x_1, x_2, \dots\}) = m(\{ x_1, x_2, \dots\}) =0 だからです。
特異連続測度とは,任意の x\in \R に対し \nu_{\mathrm{sing}}(\{x\})=0 かつ m\perp \nu_{\mathrm{sing}} をみたす測度のことです。
証明
\nu=\nu_{\mathrm{cont}}+\nu_a をルベーグ分解とする。
D = \{x\in\R\mid \nu_a(\{x\})\bigl(=\nu(\{x\})\bigr)>0\}
と定めると, D は高々可算集合である。実際,\nu はσ有限なので, \R を互いに素でかつ \nu(X_n)<\infty となる集合 \{X_n\} に分割すると,
の要素数は n \nu(X_m) 以下となる有限集合であり, D=\bigcup_{m,n=1}^\infty D_{m,n} とかけるからである。
とすると,これは離散測度である。また, \nu_{\mathrm{sing}}= \nu_a-\nu_{\mathrm{dis}} と定めると,これは明らかに連続で,かつルベーグ測度に関して特異な測度である。
一意性は簡単なので省略する。
証明終
たとえば, \R 上の確率測度は(有限測度より当然σ有限なので)この分解を用いることで,離散分布・連続分布・特異分布に分解できることが分かります。カントール分布は,特異分布として有名です。