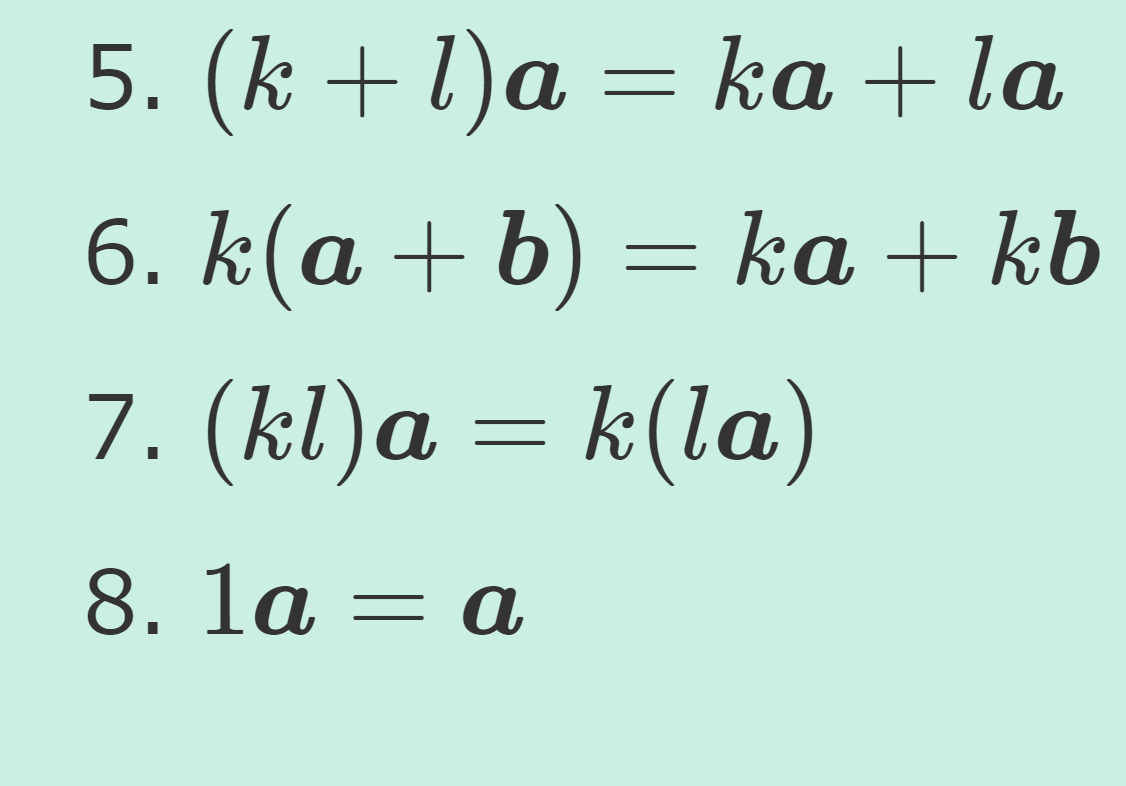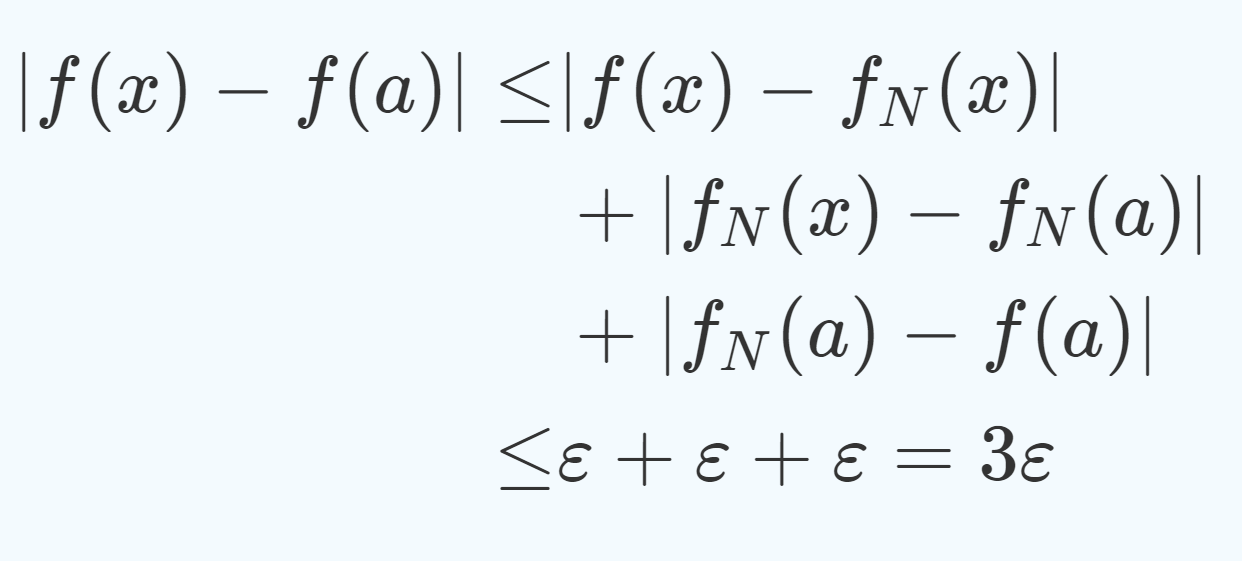ベクトル空間(線形空間,線型空間,vector space)は,高校までの,向きや大きさをもった「幾何ベクトル」と異なり難しく,簡単に理解できない概念の一つです。
本記事では,まずベクトル空間と部分ベクトル空間の定義を述べ,様々な具体例を考えることで,少しでもベクトル空間を理解することを目指します。初めての人にとっては高度な内容になるので,1回ですべて理解しようとせず,少しずつ理解していきましょう。
ベクトル空間の定義
ベクトル「空間」と言いますが,数学では「ある性質をもった”集合”」のことを「空間」と言います。すなわち,ベクトル空間とは,「ある性質をもった”集合”」なのです。どのような性質を持っているか,それが定義です。
定義(ベクトル空間)
集合 V が \mathbb{R} 上ベクトル空間(線形空間,線型空間,vector space)であるとは, V 上に以下の8つを全てみたす演算 + と \mathbb{R} 倍が定義されている集合のことである。
- (\boldsymbol{a} + \boldsymbol{b} ) + \boldsymbol{c} = \boldsymbol{a} + (\boldsymbol{b} + \boldsymbol{c})
- \boldsymbol{a} + \boldsymbol{b} = \boldsymbol{b} +\boldsymbol{a}
- \boldsymbol{0} \in V が存在して,任意の \boldsymbol{a} \in V に対して, \boldsymbol{a} + \boldsymbol{0} = \boldsymbol{0} + \boldsymbol{a} = \boldsymbol{a}, \, \boldsymbol{a} \in V となる。
- 任意の \boldsymbol{a} \in V に対して, \boldsymbol{a} + \boldsymbol{a}' = \boldsymbol{a}' + \boldsymbol{a} = \boldsymbol{0} となる \boldsymbol{a}' \in V が存在する。特にこの \boldsymbol{a}' を \boldsymbol{a}^{-1} や -\boldsymbol{a} とかく。
- (k + l) \boldsymbol{a} = k \boldsymbol{a} + l \boldsymbol{a}
- k (\boldsymbol{a} + \boldsymbol{b}) = k \boldsymbol{a} + k \boldsymbol{b}
- (kl ) \boldsymbol{a} = k (l \boldsymbol{a})
- 1 \boldsymbol{a} = \boldsymbol{a}
ただし,k,l \in \mathbb{R} とした。
また,上記の \mathbb{R} を \mathbb{C} にしたとき,これを \mathbb{C} 上ベクトル空間という。
定義だけ見てもよくわからないと思います。そもそも定義が長すぎですね。
ここでいう「演算が定義されている」とは厳密には,「写像の存在」を意味します。
演算 + , \mathbb{R} 倍が存在するとは,すなわち V には写像
\begin{gathered}
+ \colon V \times V \ni ( \boldsymbol{a}, \boldsymbol{b} ) \mapsto \boldsymbol{a} + \boldsymbol{b}\in V \\
* \colon \mathbb{R} \times V \ni (k , \boldsymbol{a}) \mapsto k \boldsymbol{a} \in V
\end{gathered}
があって,これは性質1.-8.をみたす,という意味です。(関連:二項演算・単項演算とは)難しければ「なんかそういう演算がある」と思っておいて差し支えないです。例を理解する方が大切です。
なお,本記事では \mathbb{R}, \mathbb{C} 上のベクトル空間のみ扱いますが一般には体 K 上のベクトル空間として考えることが可能です(初学者や数学専門外の方は無視してください)。
なお,定義から, (-1)\boldsymbol{a}=\boldsymbol{a}^{-1} が分かります。実際,(-1)\boldsymbol{a}+\boldsymbol{a}=(-1+1)\boldsymbol{a}=\boldsymbol{0} や \boldsymbol{a}+(-1)\boldsymbol{a}=(1-1)\boldsymbol{a}=\boldsymbol{0} が言えるからです。
部分ベクトル空間の定義
つづけて部分ベクトル空間の定義も確認しましょう。
定義(部分ベクトル空間)
V を \mathbb{R} 上ベクトル空間とし, V' \subset V とする。 V で定義されている演算 + と \mathbb{R} 倍に対して,
\begin{aligned}
\boldsymbol{a}, \boldsymbol{b} \in V' \implies \boldsymbol{a} + \boldsymbol{b} \in V' \\
k \in \mathbb{R}, \, \boldsymbol{a} \in V' \implies k\boldsymbol{a} \in V'
\end{aligned}
が成立するとき,V' はそれ自身が V と同じ演算でベクトル空間となる。これを部分ベクトル空間 (vector subspace) という。
また上記の \mathbb{R} を \mathbb{C} に変えても同じである。
ベクトル空間の部分集合が再びベクトル空間になっている場合,部分ベクトル空間というわけですね。なお,これは
k,l \in \mathbb{R}, \, \boldsymbol{a},\boldsymbol{b} \in V' \implies k\boldsymbol{a}+l\boldsymbol{b} \in V'であることと同値です。
実際,定義の2つの式を「定数倍」→「和」の順に使うと上の式が成り立ち, k=l=1 としたり, l=0 とすれば,上の1つの式から定義の2つの式が従います。
ベクトル空間・部分ベクトル空間の具体例
それでは,具体例を一つずつ確認していきましょう。
1. 平面ベクトル・空間ベクトル
高校で習った平面ベクトル・空間ベクトルは,ベクトル空間をなします。
例1.1.(平面ベクトル)
\textcolor{red}{\mathbb{R}^2 = \{ (x_1, x_2) \mid x_1, x_2 \in \mathbb{R} \}} は,演算を
\begin{gathered}
(a_1, a_2) + (b_1, b_2) = (a_1+b_1, a_2+b_2), \\
k (a_1, a_2) = (k a_1, k a_2)
\end{gathered}
と定めることで \mathbb{R} 上ベクトル空間となる。
さて,1.-8.を丁寧に確認していきましょう。
- ( (a_1, a_2) + (b_1, b_2) ) + (c_1, c_2) \\ = (a_1, a_2) + ((b_1, b_2)+(c_1, c_2)) は両辺とも (a_1+b_1+c_1, a_2+b_2+c_2) となるので成立する。
- (a_1, a_2) + (b_1, b_2) = (b_1, b_2)+(a_1, a_2) は, (a_1+b_1, a_2+b_2) = (b_1+a_1, b_2+a_2) から従う。
- (0, 0) は, \begin{aligned} (a_1, a_2) + (0,0) &= (0,0) + (a_1, a_2) \\&= (a_1, a_2) \end{aligned} となるため OK。
- 各 (a_1, a_2) に対して, (-a_1, -a_2) は (a_1, a_2) + (-a_1, -a_2) \\ = (-a_1, -a_2)+(a_1, a_2) = (0,0) となるため OK。
- (k + l) (a_1, a_2) = k (a_1, a_2) + l (a_1, a_2) は, ((k+l) a_1, (k+l) a_2) = (ka_1+la_1, ka_2+la_2) より成立する。
- k ((a_1, a_2) + (b_1, b_2)) = k (a_1, a_2) + k (b_1, b_2) は, (k(a_1+b_1), k(a_2+b_2) ) = (ka_1+ka_2, kb_1+kb_2) より従う。
- (kl ) (a_1, a_2) = k (l (a_1, a_2)) は,両辺とも (kla_1, kla_2) となるので言える。
- 1 (a_1, a_2) = (a_1, a_2) は演算の定義から明らか。
大変でしたが,以上より,ベクトル空間であることがわかりました。
例1.2.(空間ベクトル)
\textcolor{red}{\mathbb{R}^3 = \{ (x_1, x_2, x_3) \mid x_1, x_2, x_3 \in \mathbb{R} \}} は,演算を
と定めることで \mathbb{R} 上ベクトル空間となる。
これも先程と同様にすれば,ベクトル空間になることが確認できます。
2. n次元ベクトル
例2.1.(n次元ベクトル)
\textcolor{red}{\mathbb{R}^n = \{ (x_1, x_2, \ldots , x_n) \mid x_1, x_2, \ldots , x_n \in \mathbb{R} \} } は,演算を
と定めることで \mathbb{R} 上ベクトル空間となる。
いわば例1.1, 1.2 の一般化ですね。これを n 次元数ベクトルと言ったりします(→数ベクトルの定義と数ベクトルにおけるノルム・内積)。
例2.2.
\textcolor{red}{V_0 = \{ (x_1, x_2, \ldots ,x_{n-1}, 0) \mid x_1, x_2, \ldots , x_{n-1} \in \mathbb{R}\} } は, \mathbb{R}^n の部分ベクトル空間である。
これは \boldsymbol{a}, \boldsymbol{b} \in V_0, k \in \mathbb{R} に対して,明らかに \boldsymbol{a} + \boldsymbol{b}, k \boldsymbol{a} \in V_0 であることからわかります。
3. 数列
例3.1(数列)
数列全体の集合 \textcolor{red}{l(\mathbb{R}) = \{ \{a_n\} \mid a_n \in \mathbb{R} \} } は,演算を
\begin{gathered}
\{a_n\} + \{b_n\} = \{a_n + b_n\}, \\
k \{a_n\} = \{k a_n\}
\end{gathered}
と定めることで \mathbb{R} 上ベクトル空間になる。
これは,例2.1.の n 個の要素を \infty 個に拡張したものと考えられますね。
例3.2(有限個のみ0でない数列)
有限個の要素のみ非零な数列全体の集合 \textcolor{red}{l_c(\mathbb{R})= \{ \{a_n\} \mid a_n \in \mathbb{R}, \# \{ n \mid a_n \ne 0\} < \infty \} } は, l(\mathbb{R}) の部分ベクトル空間である。
少し難しいかもしれませんが,有限個のみ0でない数列の和の数列やスカラー倍をした数列は,確かに有限個のみ0でない数列であるので,これは部分ベクトル空間になります。
4. 多項式
例4.1.(多項式)
多項式全体の集合 \textcolor{red}{\mathbb{R}[x] = \{ a_nx^n + \cdots + a_1x+ a_0 \mid a_0, \ldots ,a_n \in \mathbb{R}, n \ge 1 \} } は,通常の演算によってベクトル空間となる。
「通常の演算」とは,普段行っている足し算や定数倍のことです。
5. 関数
例5.1.(関数)
関数全体の集合 \textcolor{red}{F(\mathbb{R}) = \{ f \mid f\colon \mathbb{R} \to \mathbb {R} \}} は,通常の演算によってベクトル空間となる。
例5.2.(連続関数)
連続関数全体の集合 \textcolor{red}{C(\mathbb{R}) = \{ f \mid f\colon \mathbb{R} \to \mathbb {R} \}} は, F(\mathbb{R}) の部分ベクトル空間となる。
例5.3.(無限回微分可能かつ無限遠で消滅する関数)
\textcolor{red}{C^\infty_\infty(\mathbb{R}) = \{ f\colon \mathbb{R} \to \mathbb{R} \mid f \text{ is infinitely differentiable, } \lim_{x\to \pm \infty} f(x) = 0 \} } は, C(\mathbb{R}) の部分ベクトル空間となる。
infinitely differentiable とは,「無限回微分可能」という意味です。
特に, C^\infty_\infty(\mathbb{R}) は F(\mathbb{R}) の部分ベクトル空間でもあります。
おわりに
ベクトル空間と部分ベクトル空間,その例について確認しました。最後の方の例は少し難しかったかもしれません。すべて理解できれば,自分でベクトル空間の例を作り出せるようになっていると思います。少々長い記事になってしまいましたが,少しずつ理解してもらえれば幸いです。