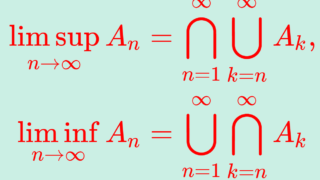PR

上極限,下極限(limsup,liminf)の定義と例と性質2つ

2021.04.26
微分積分学(大学)
用語・記号の定義大学教養
記事内に広告が含まれています。

上極限・下極限の定義をし，その具体例と重要な性質２つを確認・証明していきましょう。

数列における上極限,下極限(limsup,liminf)の定義

定義（上極限・下極限；数列版）

{an} \{a_n\} を実数列とする。このとき，

lim sup⁡n→∞an=lim⁡n→∞(sup⁡k≥nak) \color{red} \limsup_{n\to\infty} a_n = \lim_{n\to\infty}\left( \sup_{k\ge n}a_k\right)


を上極限 (limit superior) といい，

lim inf⁡n→∞an=lim⁡n→∞(inf⁡k≥nak) \color{red} \liminf_{n\to\infty} a_n = \lim_{n\to\infty} \left( \inf_{k \ge n} a_k \right)


を下極限 (limit inferior) という。

lim sup⁡n→∞an,lim inf⁡n→∞an \limsup_{n\to\infty} a_n , \liminf_{n\to\infty} a_n はそれぞれ lim‾⁡n→∞an,lim‾⁡n→∞an \varlimsup_{n\to\infty} a_n, \varliminf_{n\to\infty} a_n とかくこともある。

ここで，数列 {sup⁡k≥nak}n,{inf⁡k≥nak}n \left\{ \sup_{k\ge n}a_k\right\}_n , \left\{ \inf_{k \ge n} a_k \right\}_n はそれぞれ単調減少・単調増加ですから，上極限・下極限は ±∞ \pm\infty も含めると必ず存在することに注意しましょう(→上に有界な単調増加数列は収束することの証明)。極限とは違う性質ですね。

また，sup⁡k≥nan≥inf⁡k≥nan \sup_{k\ge n}a_n \ge \inf_{k \ge n} a_n であることと，極限の大小関係が一致することから，

lim sup⁡n→∞an≥lim inf⁡n→∞an \limsup_{n\to\infty} a_n \ge \liminf_{n\to\infty} a_n


も成り立ちます(→極限の性質6つの証明(一意性,和,積,商,大小関係))。

上極限,下極限(limsup,liminf)の具体例

具体例を挙げましょう。

例1.

an=(−1)n \color{red} a_n = (-1)^n と定めると，

lim sup⁡n→∞an=1,lim inf⁡n→∞an=−1 \limsup_{n\to\infty} a_n = 1, \quad \liminf_{n\to\infty} a_n = -1


である。

実際，sup⁡k≥nak=1, inf⁡k≥nak=−1 \displaystyle \sup_{k\ge n} a_k= 1, \, \inf_{k\ge n} a_k = -1 なので明らかですね。

例2.

an=(−1)n/n \color{red} a_n = (-1)^n /n と定めると，

lim sup⁡n→∞an=lim inf⁡n→∞an=0 \limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n = 0


である。

実際，

sup⁡k≥nak=12[n/2]→n→∞0,inf⁡k≥nak=−12[(n+1)/2]−1→n→∞0 \begin{aligned} \sup_{k\ge n} a_k&= \frac{1}{2[n/2]} \xrightarrow{n\to\infty} 0, \\ \inf_{k\ge n} a_k &=- \frac{1}{2[(n+1)/2]-1}\xrightarrow{n\to\infty} 0 \end{aligned}


(ただし[⋅][\cdot] は床関数(ガウス記号))なので，成立します。

例3.

an=n \color{red} a_n = n と定めると，

lim sup⁡n→∞an=lim inf⁡n→∞an=∞ \limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n = \infty


である。

実際，

sup⁡k≥nak=∞,inf⁡k≥nak=n→n→∞∞ \begin{aligned} \sup_{k\ge n} a_k= \infty, \quad \inf_{k\ge n} a_k =n \xrightarrow{n\to\infty} \infty \end{aligned}


のため，成立します。

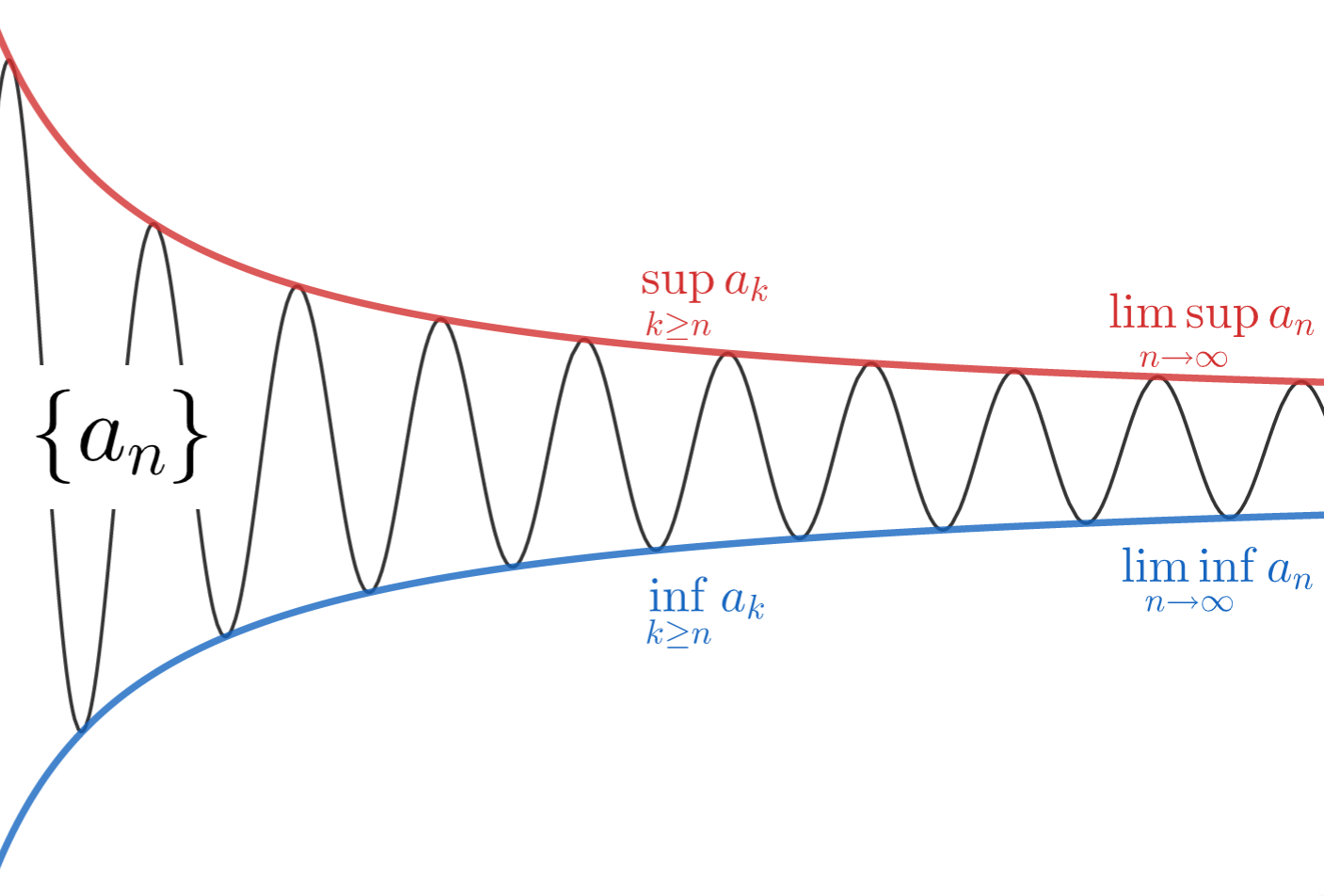
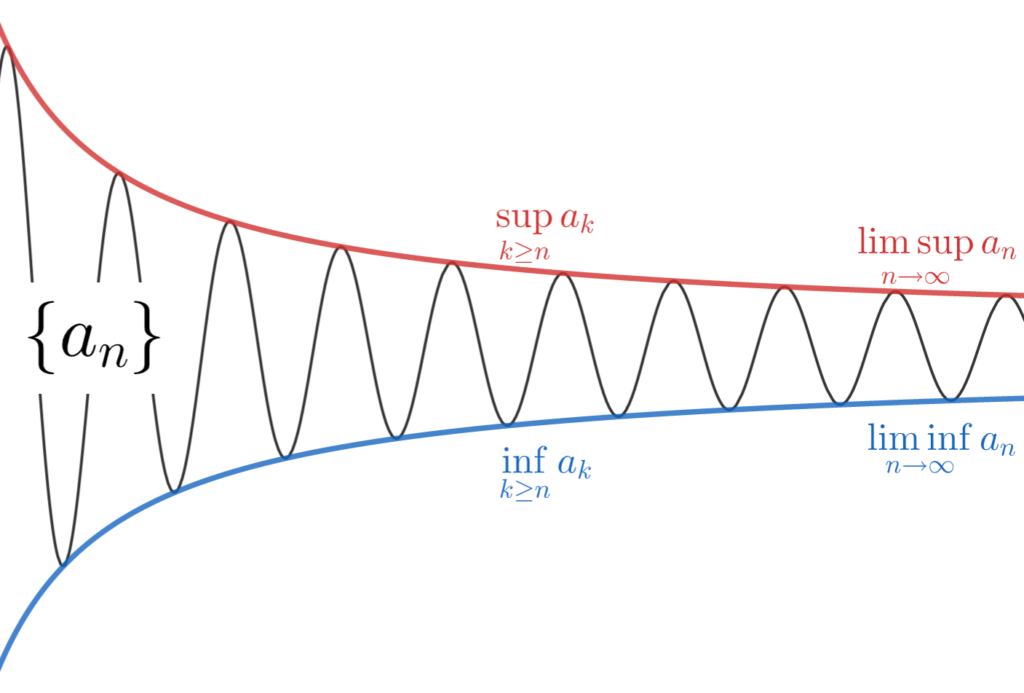
なんとなくイメージが湧いたでしょうか。図で描くと以下のようなイメージです。

limsup, liminf のイメージ

上極限,下極限(limsup,liminf)の性質

上極限・下極限の性質のうち，以下の2つ

  • 上極限・下極限に収束する部分列の存在
  • 上極限・下極限が一致 ⇒ 極限の存在

を順に確認していきましょう。

上極限,下極限に収束する部分列の存在

定理（上極限・下極限に収束する部分列の存在）

{an} \{a_n\} を実数列とし，lim sup⁡n→∞an=α,lim inf⁡n→∞an=β \limsup_{n\to\infty} a_n = \alpha, \liminf_{n\to\infty} a_n = \beta と定める。

このとき，ある部分列 {aφ1(n)},{aφ2(n)} \{ a_{\varphi_1(n)}\}, \{a_{\varphi_2(n)}\} が存在して，

lim⁡n→∞aφ1(n)=α,lim⁡n→∞aφ2(n)=β \color{red} \lim_{n\to\infty} a_{\varphi_1(n)} = \alpha, \quad \lim_{n\to\infty} a_{\varphi_2(n)} = \beta


とできる。

証明

証明では lim sup⁡ \limsup の方の α \alpha が有限のときのみ示すことにします。その他もほぼ同様だからです。

証明

φ1(1)=1\varphi_1(1) = 1 と定め φ1(n−1) \varphi_1(n-1) まで定まったとして，φ1(n) \varphi_1(n) を帰納的に定めよう。
極限の定義により，ある Nn≥1 N_n \ge 1 が存在して，

N≥Nn  ⟹  ∣sup⁡k≥Nak−α∣<1n N \ge N_n \implies\left| \sup_{k \ge N} a_k - \alpha \right| < \frac{1}{n}


とできる。とくに，N′n=max⁡{Nn,φ(n−1)} {N'}_n = \max\{ N_n, \varphi(n-1) \} と定めると，

∣sup⁡k≥N′nak−α∣<1n \left| \sup_{k \ge {N'}_n} a_k - \alpha \right| < \frac{1}{n} である。

上限(sup)の定義により，ある Kn≥N′n K_n \ge {N'}_n が存在して，

0≤sup⁡k≥N′nak−aKn≤1n 0 \le \sup_{k \ge {N'}_n} a_k - a_{K_n} \le \frac{1}{n}


とできる。φ1(n)=Kn \varphi_1(n) = K_n と定めよう。すると，

∣aφ1(n)−α∣=∣aKn−α∣≤∣aKn−sup⁡k≥N′nak∣+∣sup⁡k≥N′nak−α∣≤1n+1n=2n. \begin{aligned} &|a_{\varphi_1(n)} - \alpha | \\ &= |a_{K_n }- \alpha | \\ &\le \left|a_{K_n} - \sup_{k \ge {N'}_n} a_k \right| + \left|\sup_{k \ge {N'}_n} a_k - \alpha \right| \\ &\le \frac{1}{n} + \frac{1}{n} = \frac{2}{n}. \end{aligned}


よって lim⁡n→∞aφ(n)=α \lim_{n\to\infty} a_{\varphi(n)} = \alpha が成立する。

証明終

上極限,下極限が一致 ⇒ 極限の存在

定理（上極限・下極限が一致 ⇒ 極限の存在）

{an} \{a_n\} を実数列とする。

lim sup⁡n→∞an=lim inf⁡n→∞an=α∈[−∞,∞] \limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n = \alpha \in [-\infty, \infty]


が成立するとき，

lim⁡n→∞an=α\color{red} \lim_{n\to\infty} a_n = \alpha


である。

なおこのことから，数列の収束・発散は上極限・下極限を用いることで，以下の3つに分類されます。

極限の分類
  • lim sup⁡n→∞an=lim inf⁡n→∞an\displaystyle \limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n かつ有限値のとき lim⁡n→∞an \displaystyle \lim_{n\to\infty}a_n は収束する
  • lim sup⁡n→∞an=lim inf⁡n→∞an=±∞\displaystyle \limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n =\pm\infty のとき lim⁡n→∞an \displaystyle\lim_{n\to\infty} a_n は ±∞ \pm \infty に発散する
  • lim sup⁡n→∞an≠lim inf⁡n→∞an \displaystyle \limsup_{n\to\infty} a_n \ne \liminf_{n\to\infty} a_n のとき {an} \{a_n\} は振動する（発散する）

定理の証明をしましょう。

証明

証明では α \alpha が有限値のときのみ扱います。

証明

ε>0 \varepsilon > 0 とする。このとき，ある N≥1 N \ge 1 が存在して，

n≥N  ⟹  ∣sup⁡k≥nak−α∣<ε,n≥N  ⟹  ∣inf⁡k≥nak−α∣<ε \begin{aligned} n \ge N &\implies \left|\sup_{k\ge n}a_k - \alpha \right| < \varepsilon, \\ n \ge N &\implies \left|\inf_{k\ge n}a_k - \alpha \right| < \varepsilon \end{aligned}


とできる。inf⁡k≥nak≤an≤sup⁡k≥nak \displaystyle \inf_{k\ge n}a_k \le a_n \le \sup_{k\ge n}a_k であることに注意すると，n≥N n \ge N ならば

α−ε≤inf⁡k≥nak≤an≤sup⁡k≥nak≤α+ε \alpha - \varepsilon \le \inf_{k\ge n}a_k\le a_n \le \sup_{k\ge n}a_k \le \alpha + \varepsilon


となる。すなわち，lim⁡n→∞an=α \lim_{n\to\infty} a_n = \alpha である。

証明終

なお，はさみうちの原理を認めると，

inf⁡k≥nak≤an≤sup⁡k≥nak \inf_{k\ge n} a_k \le a_n \le \sup_{k\ge n} a_k


の各辺 n→∞ n\to\infty とすることでも証明可能ですね。

上極限集合・下極限集合

集合列に対しても上極限・下極限が定義できます。

定義（上極限集合・下極限集合・極限集合）

集合列 {An} \{A_n\} に対し，

lim sup⁡n→∞An=⋂n=1∞⋃k=n∞Ak,lim inf⁡n→∞An=⋃n=1∞⋂k=n∞Ak \color{red}\begin{gathered} \limsup_{n\to\infty} A_n =\bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k, \\ \liminf_{n\to\infty} A_n = \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k \end{gathered}


をそれぞれ上極限集合 (limit superior set)，下極限集合 (limit inferior set) という。

また，この両者が一致するとき，それを lim⁡n→∞An \color{red} \lim_{n\to\infty} A_n とかき，これを極限集合 (limit set) という。

集合列の場合であっても，数列と同じような性質が成立します。これについて詳しくは以下の記事で解説しています。

上極限集合・下極限集合の定義とその包含関係の証明
無限個の集合に対して定義される2つの極限集合（上極限集合・下極限集合）について，その定義と，日本語に直したときの意味と，包含関係の証明をします。他にも，極限集合が存在する十分条件や，数列と集合列の極限の比較も行います。
mathlandscape.com