べき級数 \sum a_n x^n におけるアーベルの定理(アーベルの連続性定理)について,その定理の主張と応用例,そして証明を述べましょう。実数の場合と複素数の場合の両方を別々に扱います。
べき級数におけるアーベルの定理【実数版】
定理(アーベルの連続性定理【実数版】)
べき級数 \displaystyle \sum_{n=0}^\infty a_n x^n の収束半径を R \in (0, \infty) とする。
\displaystyle \sum_{n=0}^\infty a_n R^n が収束するとき,べき級数の収束は [0,R] においても一様であり,したがって \displaystyle f(x) = \sum_{n=0}^\infty a_n x^n は (-R, R] 上連続である。すなわち,
\color{red}\lim_{x\to R-} \sum_{n=0}^\infty a_n x^n = \sum_{n=0}^\infty a_n .
x = -R で収束するときも同様である。
微分積分学における重要な定理の1つです。証明する前に,まずは応用例を見てみましょう。
アーベルの定理の応用例
アーベルの定理を用いれば,有名な級数の和を求めることができます。例を2つ挙げてみましょう。
例1.
\log(1+x) のマクローリン展開
\log (1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots
の収束半径は |x| < 1 である(→log(1+x)の0でのテイラー展開(マクローリン展開))。
交代級数の収束性により,右辺は x=1 で収束する。
これより,アーベルの定理から,両辺 x \to 1- (左極限)とすると
\color{red} \log 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots
がわかる。
正確な議論の流れは以下の通りです。
- 等式 \log (1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots は |x|<1 で成立する。
- 右辺で x=1 を代入した級数も収束する。
- よって,アーベルの定理より,等式の右辺について, x\to 1- としたときの値は,形式的に x=1 を代入したものに一致する。
- 左辺は x=1 で連続であるため, x\to 1- としたものと x=1 を代入したものは同じである。
- 3,4より,結果的に元の等式は x=1 を代入しても成立する。
もう一つ例を挙げてみましょう。
例2.
\tan^{-1} x = x-\frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots
の収束半径は |x|<1 である。交代級数の収束性により,右辺は x=1 で収束する。
これより,アーベルの定理から,両辺 x \to 1- (左極限)とすると
\color{red} \frac{\pi}{4} = 1- \frac{1}{3} +\frac{1}{5} - \frac{1}{7} + \cdots
がわかる。
同じく,正確な議論を書き下してみましょう。
- 等式 \tan^{-1} x = x-\frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots は |x|<1 で成立する。
- 右辺で x=1 を代入した級数も収束する。
- よって,アーベルの定理より,等式の右辺について, x\to 1- としたときの値は,形式的に x=1 を代入したものに一致する。
- 左辺は x=1 で連続であるため, x\to 1- としたものと x=1 を代入したものは同じである。
- 3,4より,結果的に元の等式は x=1 を代入しても成立する。
アーベルの定理【実数版】の証明
さて,アーベルの定理(アーベルの連続性定理)を証明してみましょう。
証明
まず収束半径が R=1 で, x=1 で収束する場合を示す。
\varepsilon > 0 とする。仮定より, \sum a_n は収束するから,ある N \ge 1 が存在して, n\ge m \ge N ならば
\left|\sum_{k=m}^n a_k \right| < \varepsilon
が成立する(コーシー列)。ここで, m \ge N を任意に一つ固定して, s_n = \sum_{k=m}^n a_k と定めよう。すると,任意の 0 \le x \le 1 に対して,
となり,よって \{\sum_{k=1}^n a_k x^k\}_n は [0,1] 上の一様コーシー列である。従って,べき級数 \sum a_n x^n は [0,1] 上一様収束し,連続関数の一様収束極限は連続であるから, 連続性もわかる。
一般の R の場合では,べき級数の x を Rx に置換することで同様である。
証明終
無事に証明できましたね。
べき級数におけるアーベルの定理【複素数版】
複素関数論におけるアーベルの連続性定理も紹介・証明しておきましょう。
定理(アーベルの連続性定理【複素数版】)
べき級数 \displaystyle \sum_{n=0}^\infty a_n z^n の収束半径を R \in (0, \infty) とする。
\displaystyle \sum_{n=0}^\infty a_n R^n が収束するとき, z が |z|<R かつ |R-z|/(R-|z|) が有界であるようにして, z\to R となるならば, \displaystyle \sum_{n=0}^\infty a_n z^n は \displaystyle \sum_{n=0}^\infty a_n R^n に収束する。
z = Re^{i\theta} で収束するときも同様である。
|R-z|/(R-|z|) が有界であるようにして,という点が少し曲者ですね。これは「ストルツの角 (Stolz angle) から近づく」という言い方をすることもあります。
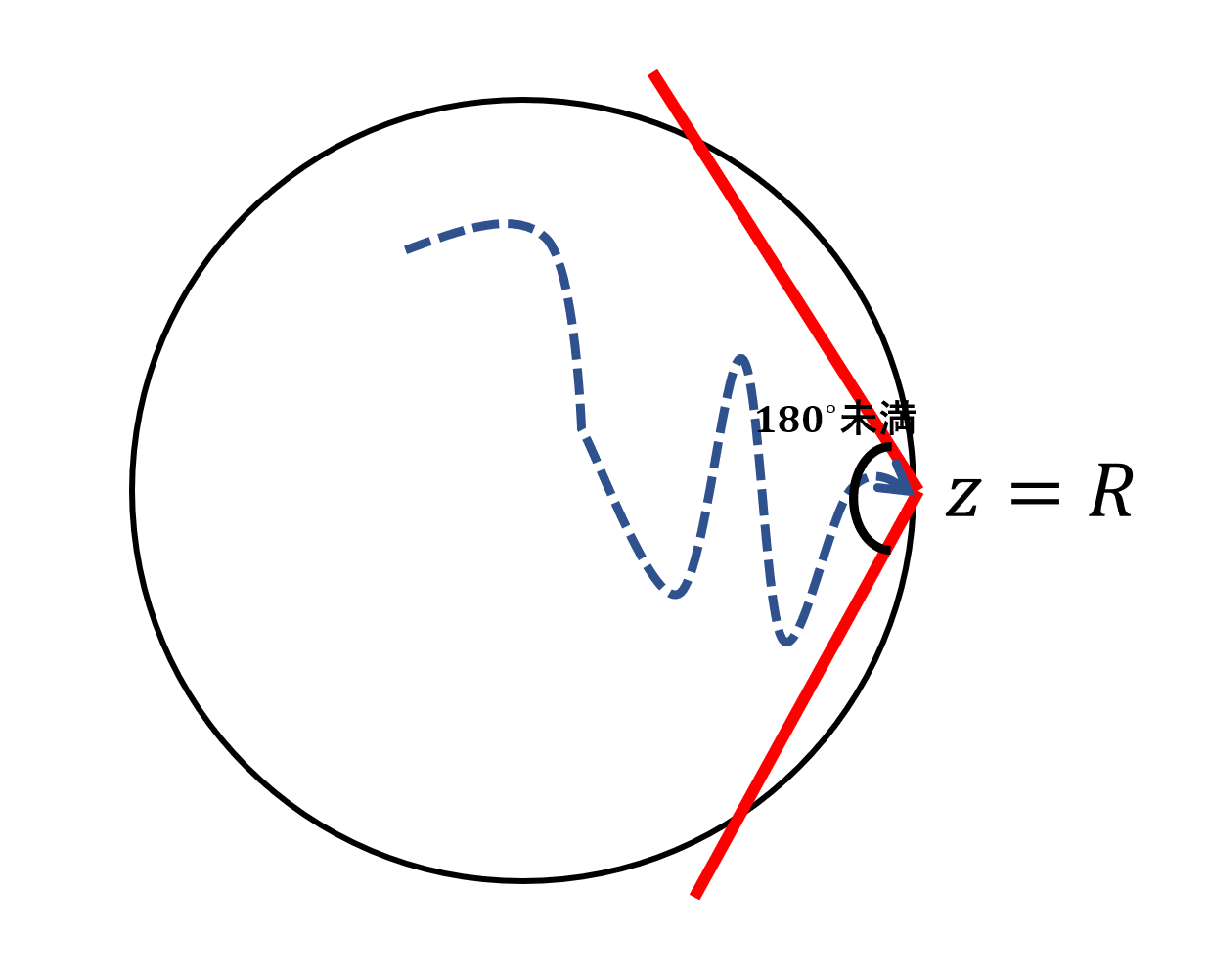
これは,図形的に解釈すると「実軸上の部分 (-\infty, R) に対し対称な角領域で,R を頂点とし,角が 180^\circ より小さいものの中に z がある」ということです。図で描くと以下のような感じです。
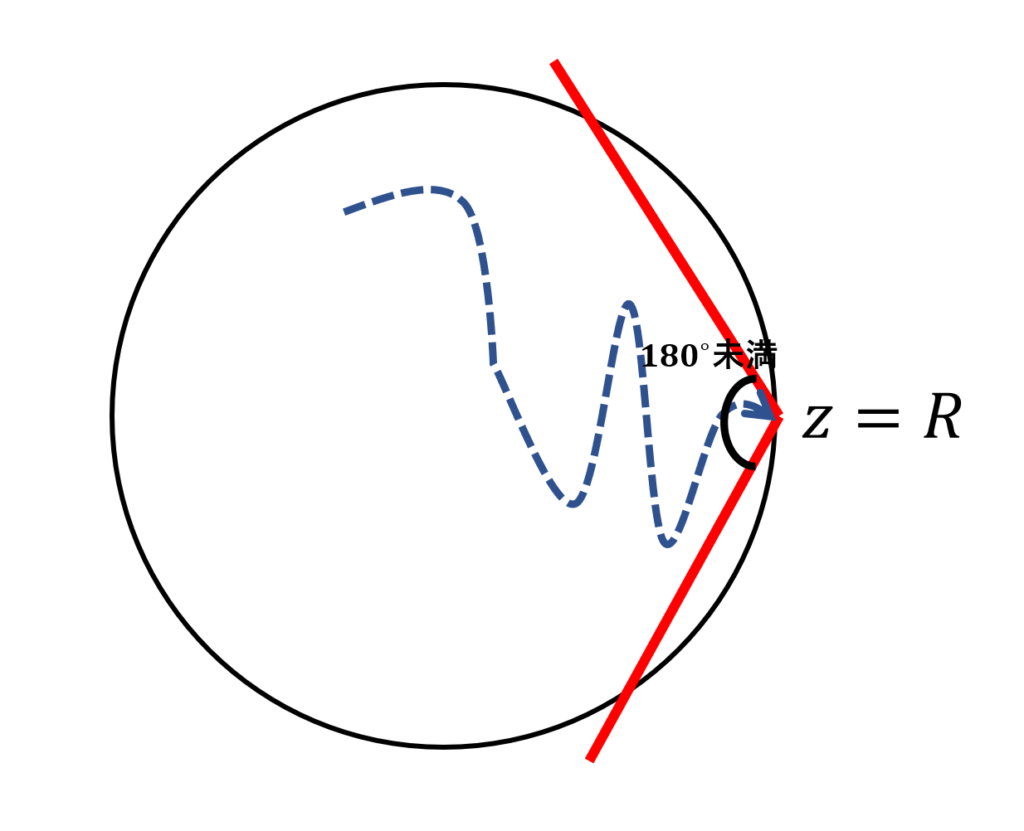
複素数版のアーベルの定理の証明
複素数版の証明も与えておきましょう。方針は実数のときとほぼ同じです。
証明
まず収束半径が R=1 で, z=1 で収束する場合を示す。
\varepsilon > 0 とする。仮定より, \sum a_n は収束するから,ある N \ge 1 が存在して, n\ge m \ge N ならば
\left|\sum_{k=m}^n a_k \right| < \varepsilon
が成立する(コーシー列)。ここで, m \ge N を任意に一つ固定して, s_n = \sum_{k=m}^n a_k と定めよう。すると,「 |z|<1 または z=1 」かつ「 |1-z|\le K(1-|z|) 」をみたす任意の z に対して,
となり,よって \{\sum_{k=1}^n a_k z^k\}_n は 「 |z|<1 または z=1 」かつ「 |1-z|\le K(1-|z|) をみたす z の領域上の一様コーシー列である。従って,べき級数 \sum a_n z^n は この上で一様収束し,連続関数の一様収束極限は連続であるから, 連続性もわかる。
一般の R の場合では,べき級数の z を Rz に置換することで同様である。
証明終