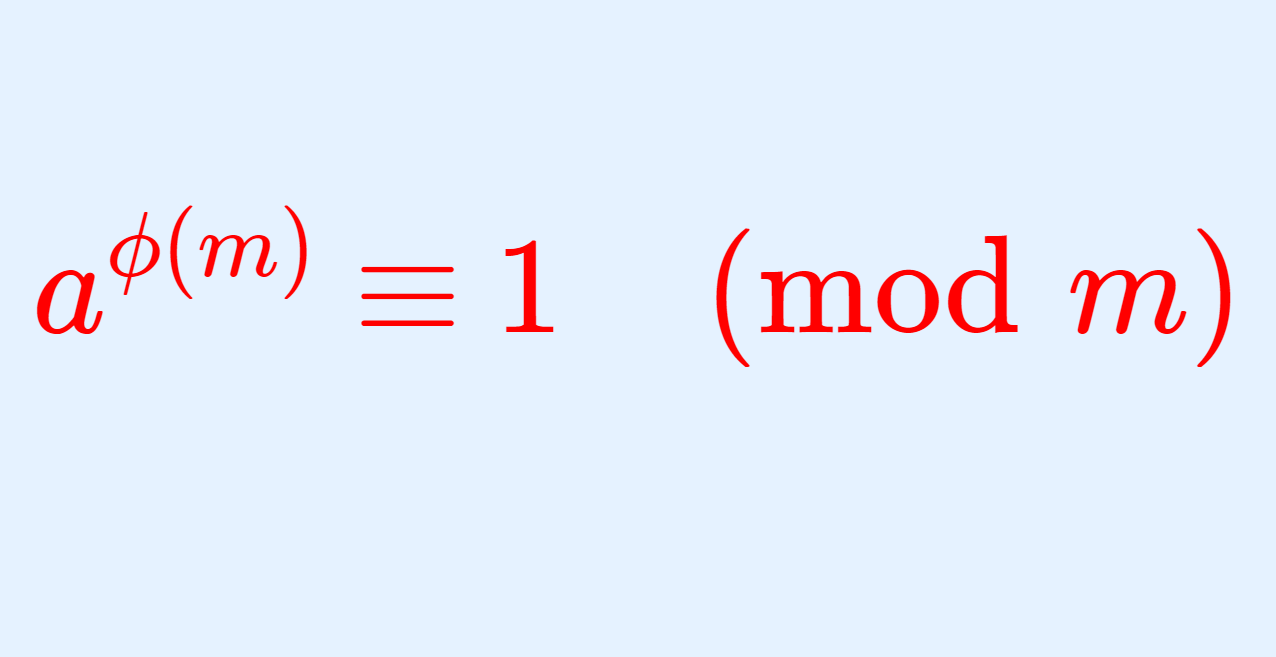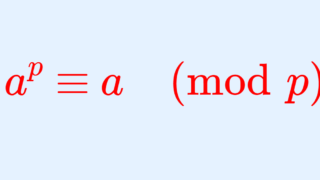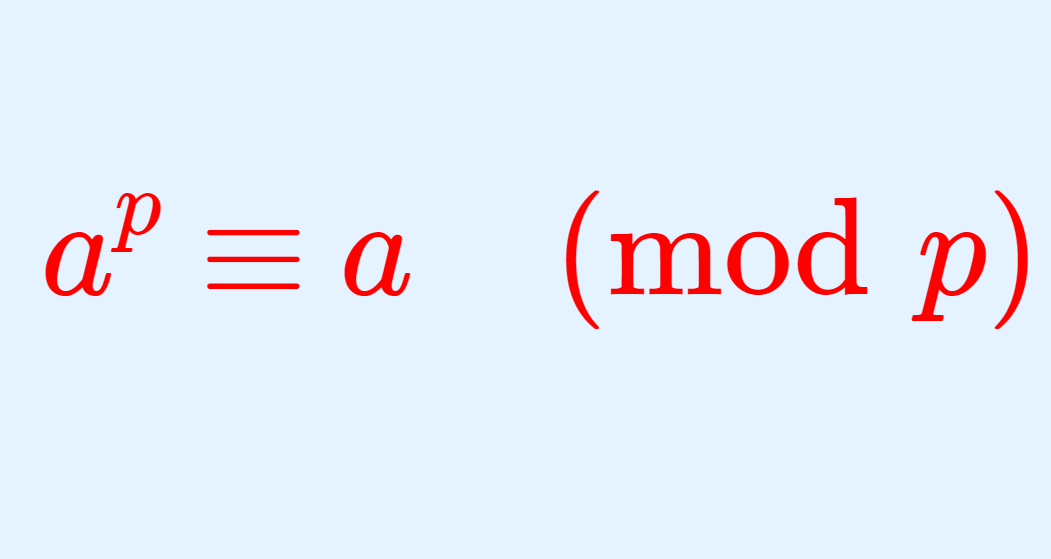数論(整数論)において,フェルマーの小定理の一般化である「オイラーの定理」について,その定理の主張と証明を解説しましょう。
数論におけるオイラーの定理
「オイラー」の名前が付く定理や公式はいろいろありますが,今回は数論(整数論)に関するものです。
オイラーの定理 (Euler’s theorem)
\phi(n) を, 1,2,\dots, n-1 のうち, n と互いに素なものの個数とする(オイラーの \phi 関数という)。
m\ge 2 を整数, a を m と互いに素な整数とする。このとき,
\large\color{red} a^{\phi(m)} \equiv 1 \pmod m
である。
この定理は,フェルマーの小定理の一般化になっています。実際, m=p を素数とすると, \phi(m)=p-1 となって,定理の主張は
a^{p-1} \equiv 1 \pmod p
となって,フェルマーの小定理ですね。フェルマーの小定理は,以下でも別途解説しています。
注意ですが, \phi(m) は a^n\equiv 1 をみたす正の整数 n で,最小のものとは限りません。
オイラーの定理の2通りの証明
早速証明しましょう。
- 初等的な整数論を用いた証明
- 群論におけるラグランジュの定理を用いた専門的な証明
の順に紹介します。
初等的な整数論を用いた証明
証明
S=\{x_1,x_2,\dots, x_{\phi(m)}\} \subset \{ 1,2,\dots, m-1\} を, m と互いに素な集合とする。すると, a x_i も m と互いに素なので, ax_i\equiv x_j \pmod m となる x_j\in S が存在する。
ここで, ax_1, ax_2, \dots, ax_{\phi(m)} を m で割った余りはどの2つも異なる。実際, ax_i \equiv ax_{i'}\pmod m とすると, a は m と互いに素なので,両辺 a で割れて, x_i\equiv x_{i'}\pmod m だからである。
従って, ax_1, ax_2, \dots, ax_{\phi(m)} を m で割った余りには, x_1, x_2, \dots, x_{\phi(m)} が1回ずつ現れる。ゆえに \mod m で
ax_1 ax_2 \dots ax_{\phi(m)} \equiv x_1 x_2\dots x_{\phi(m)}.
すなわち
である。積 x_1x_2\dots x_{\phi(m)} は m と互いに素なので,両辺割り算できて,
を得る。
証明終
頑張れば高校生にも理解できる証明でしょう。
群論におけるラグランジュの定理を用いた専門的な証明
さて,もう一つ,群論におけるラグランジュの定理を用いた証明を紹介します。ここでは,少々代数の専門的な知識が必要です。
証明
環 \mathbb{Z}/m\mathbb{Z} の乗法群 (\mathbb{Z}/m\mathbb{Z})^{\times} の位数は \phi(m) である。
ラグランジュの定理より,元 a\in (\mathbb{Z}/m\mathbb{Z})^{\times} の位数 d は,群の位数の約数であるから, \phi(m)= d x ( x は正の整数) とかける。従って,
a^{\phi(m)} \equiv a^{dx}\equiv 1^x \equiv 1 \pmod m
を得る。
証明終
鮮やかですっきりした証明ですね。