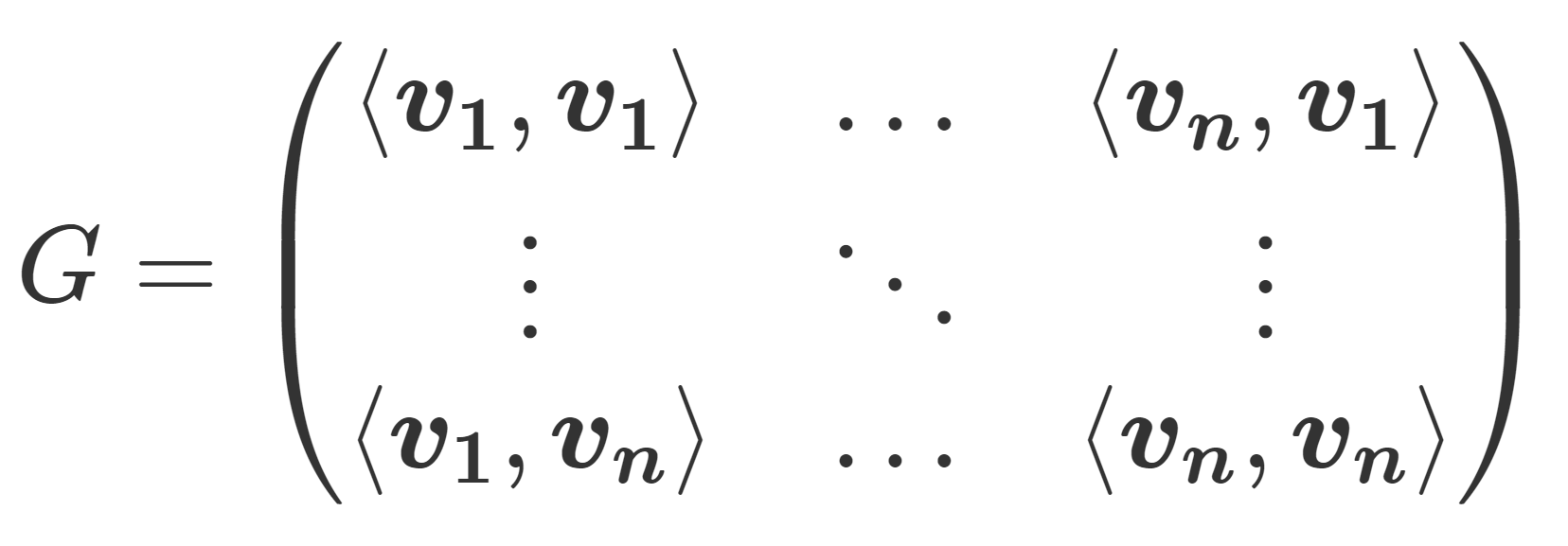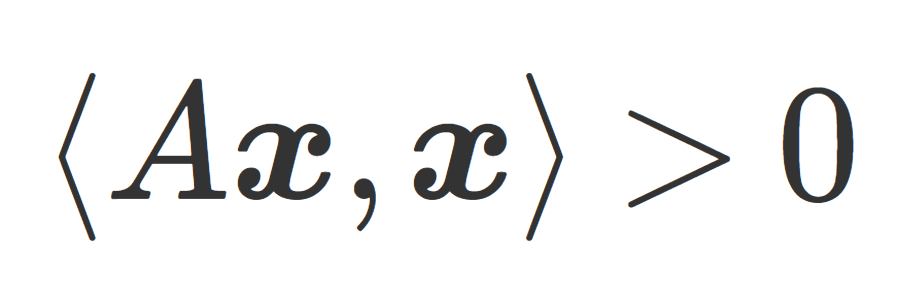グラム行列とは, (i, j) 成分がベクトル \boldsymbol{x_i},\boldsymbol{x_j} の内積になる行列のことです。これについて,定義と性質を証明付きで解説しましょう。
グラム行列とは
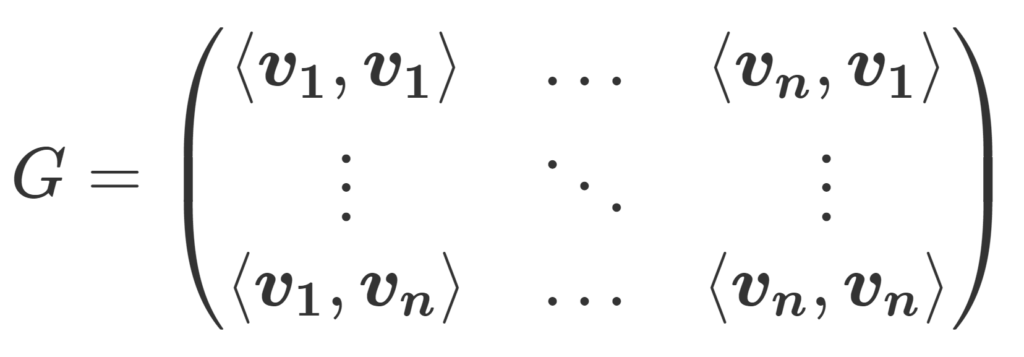
定義(グラム行列)
数ベクトル \boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_n}\in\mathbb{C}^n に対し,(i,j) 成分が \boldsymbol{v_i} と \boldsymbol{v_j} の内積となる行列 \color{red} G = (\langle \boldsymbol{v_i}, \boldsymbol{v_j}\rangle) ,すなわち
\color{red} G= \begin{pmatrix}\langle \boldsymbol{v_1},\boldsymbol{v_1}\rangle & \dots & \langle \boldsymbol{v_n},\boldsymbol{v_1}\rangle \\ \vdots & \ddots &\vdots \\ \langle \boldsymbol{v_1},\boldsymbol{v_n}\rangle &\dots & \langle \boldsymbol{v_n},\boldsymbol{v_n}\rangle \end{pmatrix}
となる行列をグラム行列 (Gram matrix) という。 A = (\boldsymbol{v_1}, \boldsymbol{v_2}, \dots , \boldsymbol{v_n}) を n 次正方行列とすると,
と表せる。 A^* は A の随伴行列(共役転置)を指す。
\boldsymbol{x} = \begin{pmatrix} x_1 \\ \vdots \\ x_n\end{pmatrix}, \boldsymbol{y} = \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix} \in\mathbb{R}^n に対し,内積は
\langle \boldsymbol{x}, \boldsymbol{y}\rangle = \sum_{k=1}^n x_k \overline{y}_k = \boldsymbol{y}^*\boldsymbol{x}
です。 \overline{y}_k は y_k の複素共役です。
\boldsymbol{v_1}, \boldsymbol{v_2},\dots, \boldsymbol{v_n}\in\mathbb{R}^n のとき, A は実行列ですから,
\color{red} \Large G = A^\top A
と表せます。
グラム行列の主な性質
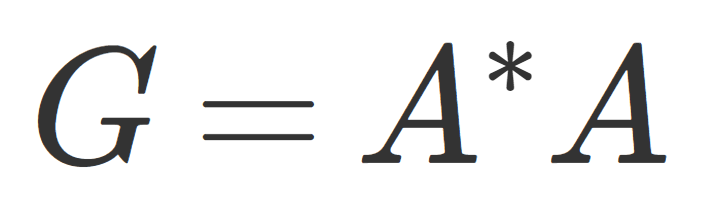
定理(グラム行列の性質)
G = A^*A をグラム行列とする。このとき,
また逆に,半正定値エルミート行列はグラム行列になることが知られています(証明は正定値行列・半正定値行列の定義・性質3つとその証明で行っています)。
順番に確認していきましょう。
1. グラム行列はエルミート行列であること
A がエルミート行列であるとは, A^* =A が成立することを指します(→エルミート行列の定義と性質4つとその証明)。
証明
一般に正方行列 A,B に対し, (AB)^* = B^* A^* である(→随伴行列(エルミート転置,共役転置)の定義と性質10個)。
(A^* A)^* =A^* (A^*)^* = A^* A
より, A^*A はエルミート行列である。
証明終
グラム行列はエルミート行列ですから,エルミート行列で成立するすべての性質が成立します。これについては,以下で解説しています。
2. グラム行列は半正定値行列であること
エルミート行列 A が半正定値行列とは,任意の列ベクトル \boldsymbol{x}\in\mathbb{C}^n に対し,
\langle A\boldsymbol{x}, \boldsymbol{x} \rangle = \boldsymbol{x}^* A\boldsymbol{x} \ge 0
となることを言います(→正定値行列・半正定値行列の定義・性質3つとその証明)。
証明
一般に n 次正方行列 A とベクトル \boldsymbol{x},\boldsymbol{y}\in\mathbb{C}^n に対し, \langle A\boldsymbol{x}, \boldsymbol{y}\rangle = \langle \boldsymbol{x}, A^* \boldsymbol{y} \rangle が成り立つことに注意する(→随伴行列(エルミート転置,共役転置)の定義と性質10個)。よって,
\begin{aligned} \langle G\boldsymbol{x}, \boldsymbol{x} \rangle &= \langle A^*A \boldsymbol{x}, \boldsymbol{x} \rangle \\ &= \langle A\boldsymbol{x}, A\boldsymbol{x} \rangle\\&= \lVert A\boldsymbol{x} \rVert ^2 \ge 0. \end{aligned}証明終
3. グラム行列は行列式が非負の実数であること
証明
行列式の性質(行列式の性質6つの証明(列,行の線形性,置換,積,転置など))より,
\begin{aligned} \det G &= \det A^* A = \det A^*\det A \\&= \overline{\det A} \det A \\&= |\det A|^2 \ge 0. \end{aligned}証明終