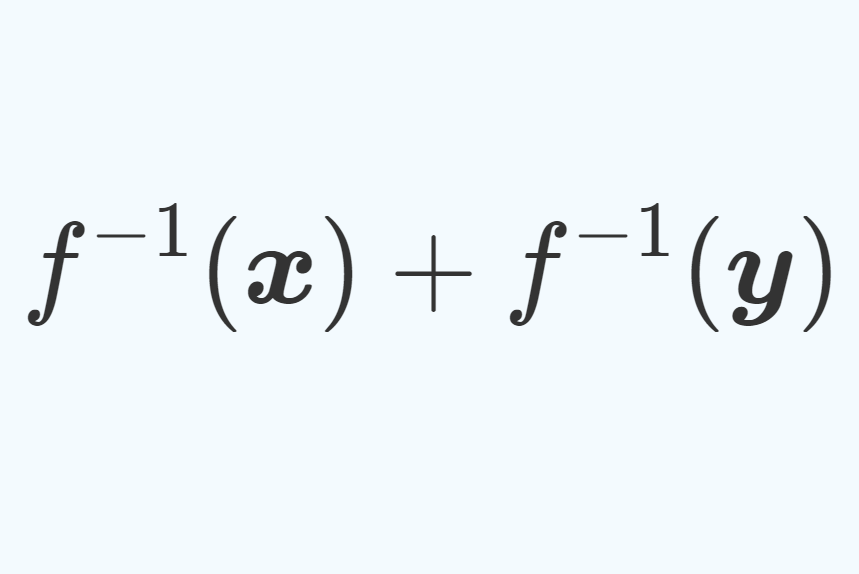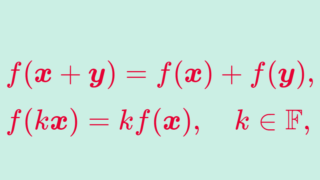線形同型写像とは,全単射な線形写像を指します。このような写像が存在する2つのベクトル空間は同型であるといい,全く同じものとして扱うことが可能です。
線形同型写像とベクトル空間の同型について,基本的なことをおさえましょう。
線形同型写像とベクトル空間の同型
まず定義の前に線形写像の復習をしておきましょう。線形写像とは以下をみたす写像です。
- f(\boldsymbol{x}+\boldsymbol{y}) = f(\boldsymbol{x})+f(\boldsymbol{y})
- f(k\boldsymbol{x})=kf(\boldsymbol{x})
詳しくは以下で解説しています。
これをもとに,定義を述べましょう。
定義(線形同型写像・ベクトル空間の同型)
V,W をベクトル空間とし, f\colon V\to W を線形写像とする。
f が全単射であるとき,自動的に f^{-1} も線形写像になる(※)。このとき, f を線形同型 (linear isomorphism) という。
ベクトル空間 V,W の間に線形同型写像が存在するとき, V,W は同型 (isomorphic) といい, \color{red}V\simeq W や \color{red} V\cong W などとかく。
ベクトル空間が同型であるとは,ベクトル空間として全く同じものと考えられるということです。数学においては,この「同型」という考え方は非常に大切です。
定義の※の部分の証明をしておきましょう。
定義の※の証明
V,W を \mathbb{F} 上のベクトル空間とする。
f\colon V\to W が同型であるとき, f^{-1}\colon W\to V が全単射であることは明らかであるから, f^{-1} が線形写像になることを示せばよい。
\boldsymbol{x},\boldsymbol{y}\in W とする。このとき, f\circ f^{-1} は恒等写像で, f は線形写像であるから,
\begin{aligned}\boldsymbol{x}+\boldsymbol{y} &= f\circ f^{-1} ( \boldsymbol{x}+\boldsymbol{y} ) ,\\ \boldsymbol{x}+\boldsymbol{y} &= f\circ f^{-1} (\boldsymbol{x})+ f\circ f^{-1} (\boldsymbol{y}) \\ &= f(f^{-1} (\boldsymbol{x})+f^{-1}(\boldsymbol{y})) \end{aligned}
が成立する。よって, f\circ f^{-1} ( \boldsymbol{x}+\boldsymbol{y} ) = f(f^{-1} (\boldsymbol{x})+f^{-1}(\boldsymbol{y}) ) であり,両辺 f^{-1} でうつすと,
となる。また, k\in \mathbb{F} とすると,
なので, f\circ f^{-1} (k\boldsymbol{x}) = f(kf^{-1}(\boldsymbol{x})) がわかる。両辺 f^{-1} でうつすと,
となる。ゆえに f^{-1} は線形写像である。
証明終
同型なベクトル空間の性質
同型なベクトル空間の性質を挙げましょう。
定理(同型なベクトル空間)
U, V,W をベクトル空間とする。このとき,
- U\simeq V ならば \dim U = \dim V (次元)。逆に, \dim U =\dim V<\infty ならば U\simeq V である。
- U\simeq U (反射律)
- U \simeq V\implies V\simeq U (対称律)
- U \simeq V,\, V\simeq W\implies U\simeq W (推移律)
特に,2-4.より「同型」という関係は同値関係である。
同値関係とは,まさに「同じものと思える関係」です。ベクトル空間が同型なら,それは全く同じものと思えます。
特に,1.の逆に以降より, V を \mathbb{R} 上の n<\infty 次元ベクトル空間とすると,\color{red} V\simeq \mathbb{R}^n がわかります。
証明
1.の U\simeq V\implies \dim U = \dim V について
f\colon U\to V を同型写像とする。次元定理
\dim U = \dim\operatorname{Ker} f+ \operatorname{rank} f
について,いまの場合単射より \operatorname{Ker} f= \{\boldsymbol{0}\} (→線形写像が単射になる必要十分条件は核(Ker)が0になる証明)なのと,全射より \operatorname{rank} f= \dim \operatorname{Im} f = \dim V が成り立つため,直ちに \dim U = \dim V がわかる。
1.の \dim U=\dim V<\infty \implies U\simeq V について
\dim U = \dim V = n とし, U,V の基底をそれぞれ \boldsymbol{u_1},\dots, \boldsymbol{u_n}, \boldsymbol{v_1},\dots, \boldsymbol{v_n} とする。このとき,
f\left(\sum_{j=1}^n k_j \boldsymbol{u_j}\right) = k_j \boldsymbol{v_j}
と定めると,これは線形同型写像である(演習問題とする)。よって U\simeq V である。
2. U\simeq U について
恒等写像は同型写像であるからわかる。
3. U \simeq V\implies V\simeq U について
f が同型写像のとき, f^{-1} もそうであることは上の「※の証明」で示したとおりであるからわかる。
4. U \simeq V,\, V\simeq W\implies U\simeq W について
f\colon U\to V, \, g\colon V\to W が同型写像であるとき, g\circ f\colon U\to W が同型であることは簡単にわかるので,従う。
証明終