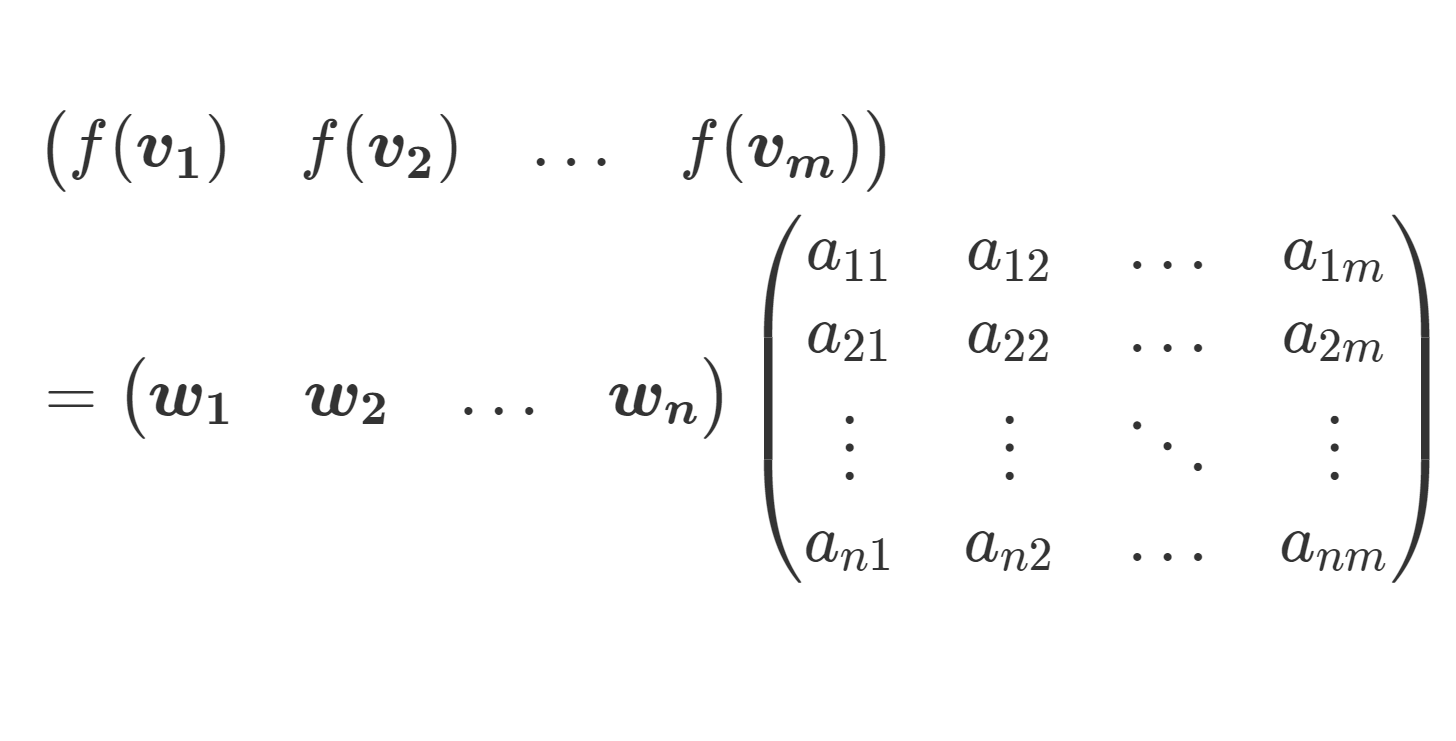線形写像と行列の間には,非常に深い関係があります。それは,線形写像は行列を用いて表現することができるというものです。このことについて,具体例も交えながら紹介していきましょう。
【表現行列】線形写像の行列表示
V, W をそれぞれ m,n 次元ベクトル空間とし,その基底を \{\boldsymbol{v_1},\boldsymbol{v_2},\ldots, \boldsymbol{v_m}\}, \;\{\boldsymbol{w_1},\boldsymbol{w_2},\ldots, \boldsymbol{w_n}\} と定めます。このとき, V, W の全ての元は,基底の一次結合でかけることに注意しましょう。
ここで, f\colon V \to W を線形写像とします。すると,
\begin{aligned} f(\boldsymbol{v_1}) &= a_{11}\boldsymbol{w_1}+a_{21}\boldsymbol{w_2}+\cdots+ a_{n1}\boldsymbol{w_n}, \\ f(\boldsymbol{v_2}) &= a_{12}\boldsymbol{w_1}+a_{22}\boldsymbol{w_2}+\cdots+ a_{n2}\boldsymbol{w_n}, \\ \cdots &\\ f(\boldsymbol{v_m}) &= a_{1m}\boldsymbol{w_1}+a_{2m}\boldsymbol{w_2}+\cdots+ a_{nm}\boldsymbol{w_n}. \\ \end{aligned}
と定めることができます。(線形写像は,基底の行先を決めるだけで,すべての元の行先が決まることに注意しましょう。実際, f(c_1\boldsymbol{v_1}+\cdots + c_m\boldsymbol{v_m} ) = c_1f(\boldsymbol{v_1}) +\cdots+ c_m f(\boldsymbol{v_m}) を用いればよいです)
上の m 個の式は,行列の積を考えると, n \times m 行列を用いて,形式的に
\begin{aligned} &\begin{pmatrix} f(\boldsymbol{v_1}) & f(\boldsymbol{v_2}) & \dots & f(\boldsymbol{v_m}) \end{pmatrix} \\ &= \begin{pmatrix} \boldsymbol{w_1} & \boldsymbol{w_2} & \dots & \boldsymbol{w_n} \end{pmatrix} \begin{pmatrix}a_{11} & a_{12} & \dots & a_{1m} \\ a_{21}& a_{22} & \dots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}& a_{n2} & \dots& a_{nm} \end{pmatrix} \end{aligned}
とかくことができます。このときの, n \times m 行列 A=(a_{ij}) を f の表現行列(行列表示)といいます。
ちゃんと定義をまとめておきましょう。
【表現行列】線形写像の行列表示の定義
定義(線形写像の表現行列)
V, W を m,n 次元ベクトル空間とし, その基底を \{\boldsymbol{v_1},\boldsymbol{v_2},\ldots, \boldsymbol{v_m}\}, \{\boldsymbol{w_1},\boldsymbol{w_2},\ldots, \boldsymbol{w_n}\} とする。
線形写像 f\colon V\to W に関して,これらの基底を用いて
とかけるとき,このときの n\times m 行列 A を f の表現行列(行列表示)という。
ここで,表現行列は基底の取り方に依存することに注意しましょう。
全ての線形写像は,基底を定めるごとに表現行列を取ることができ,逆に基底と n\times m 行列を定めると,それをもとに線形写像 f \colon V\to W を取ることが可能です。
とにかく,表現行列とは,
\color{red} ( f(\boldsymbol{v_1}) , f(\boldsymbol{v_2}) , \dots , f(\boldsymbol{v_m}) )= ( \boldsymbol{w_1} , \boldsymbol{w_2} , \dots , \boldsymbol{w_n}) A
となる行列 A のことだ,と覚えてもよいでしょう。
表現行列の求め方の具体例
例題1.
V, W の基底を \{\boldsymbol{v_1},\boldsymbol{v_2}\}, \; \{ \boldsymbol{w_1},\boldsymbol{w_2},\boldsymbol{w_3}\} とし,
\begin{aligned} f(\boldsymbol{v_1}) &= 2\boldsymbol{w_1} - \boldsymbol{w_3}, \\ f(\boldsymbol{v_2}) &= 3\boldsymbol{w_2}+\boldsymbol{w_3} \end{aligned}
であるとする。このときの f の行列表示を答えよ。
ですから,求める行列表示は \color{red} \begin{pmatrix} 2 & 0 \\ 0 & 3 \\ -1 & 1 \end{pmatrix} ですね。
例題2.
例題1において, V の基底を
\begin{aligned}\boldsymbol{v'_1} &= \boldsymbol{v_1}, \\ \boldsymbol{v'_2} &= \boldsymbol{v_1}+\boldsymbol{v_2} \end{aligned}
とし, W の基底を
としたときの行列表示を求めよ。
上より,
\begin{aligned}\boldsymbol{w_1} &= \boldsymbol{w'_1}, \\ \boldsymbol{w_2} &= \boldsymbol{w'_2}-\boldsymbol{w'_1} , \\ \boldsymbol{w_3}&= \boldsymbol{w'_3}-\boldsymbol{w'_2}\end{aligned}
ですから,
となり,結局,
です。したがって,求める行列表示は \color{red} \begin{pmatrix}2 & -1 \\ 1 & 3 \\ -1 & 0 \end{pmatrix} ですね。このように,基底を変えると,表現行列は変わります。
なお,基底の変換も行列でかけます。それを用いれば,今回の表現行列は,例題1の答えと,その行列との積でかけることが知られています。これについては,以下で解説しています。
例題3.
A = \begin{pmatrix} 1 & 0 \\ -1 & 2 \end{pmatrix} に対し,線形写像 f\colon \mathbb{R}^2\to \mathbb{R}^2 を
f\colon \begin{pmatrix} x \\ y \end{pmatrix} \mapsto A \begin{pmatrix} x \\ y \end{pmatrix}
と定める。このとき, \left\{ \begin{pmatrix} 1\\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right\} を \mathbb{R}^2 の基底としたときの, f の行列表示を求めよ。
\boldsymbol{e_1} = \begin{pmatrix} 1\\ 0 \end{pmatrix} , \; \boldsymbol{e_2} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} と定めると,今回の写像は
\begin{pmatrix} f(\boldsymbol{e_1}) & f(\boldsymbol{e_2}) \end{pmatrix} = \begin{pmatrix} \boldsymbol{e_1} & \boldsymbol{e_2} \end{pmatrix} \begin{pmatrix} 1 & 0 \\ -1 & 2 \end{pmatrix}
となることが分かりますから,求める行列表示は, \color{red} A そのものになりますね。
表現行列(線形写像の行列表示)の性質
表現行列の性質を2つ紹介しましょう。
成分表示と表現行列
基底などの表記は定義のものを適用することし,以下には書かないことにします。
定理(成分表示と表現行列)
線形写像 f\colon V\to W の表現行列を A とする。加えて, \boldsymbol{x} \in V に対し, \boldsymbol{y} = f(\boldsymbol{x}) であり,これらは基底を用いて
\begin{aligned} \boldsymbol{x} &= x_1\boldsymbol{v_1}+x_2\boldsymbol{v_2} + \dots + x_m \boldsymbol{v_m} , \\ \boldsymbol{y} &= y_1\boldsymbol{w_1}+y_2\boldsymbol{w_2}+\dots + y_n\boldsymbol{w_n} \end{aligned}
と表せるとする。このとき,
である。
成分表示の係数だけ見て,各元の行先を考えられるということですね。
証明
\begin{aligned} & \begin{pmatrix} \boldsymbol{w_1}& \dots & \boldsymbol{w_n}\end{pmatrix} \begin{pmatrix} y_1 \\ \vdots \\ y_n\end{pmatrix}\\ &= \boldsymbol{y} = f(\boldsymbol{x}) \\ &= f(x_1\boldsymbol{v_1}+\cdots + x_m \boldsymbol{v_m}) \\ &= x_1f(\boldsymbol{v_1})+\cdots x_m f(\boldsymbol{v_m}) \\ &= \begin{pmatrix} f(\boldsymbol{v_1}) & \dots f(\boldsymbol{v_m}) \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\ x_m \end{pmatrix} \\ &= \begin{pmatrix} \boldsymbol{w_1}& \dots & \boldsymbol{w_n}\end{pmatrix} A \begin{pmatrix} x_1 \\ \vdots \\ x_m \end{pmatrix} \end{aligned}
であるから,
である。
証明終
線形写像の合成と表現行列の積
定理(線形写像の合成は表現行列の積である)
U,V,W をそれぞれ \{ \boldsymbol{u_1}, \dots ,\boldsymbol{u_l}\}, \; \{ \boldsymbol{v_1}, \dots ,\boldsymbol{v_m}\}, \; \{ \boldsymbol{w_1}, \dots ,\boldsymbol{w_n}\} を基底とするベクトル空間とし, f\colon U\to V,\; g\colon V\to W を線形写像とする。
f, g の表現行列を A_f, A_g とし,線形写像 g\circ f の表現行列を A_{g\circ f } とするとき,
\color{red}A_{g\circ f} = A_g A_f
が成立する。
線形写像の合成は,表現行列の積に対応しているということですね。
最初に行列の積の定義を見たとき,理解し難いものがあったと思います。行列はそもそも,線形写像を表すツールだと思うと,「行列の積は,線形写像の合成に対応するように定められている」と考えることができ,非常に合理的なわけです。
証明しましょう。
証明
関数 h に対して,( h(\boldsymbol{v_1}), \ldots ,h(\boldsymbol{v_m} )) を単に h(\boldsymbol{v_1}, \ldots , \boldsymbol{v_m}) とかくことにしよう。
\begin{aligned} f\colon (\boldsymbol{u_1},\dots, \boldsymbol{u_l})&\mapsto (\boldsymbol{v_1},\dots, \boldsymbol{v_m})A_f, \\ g\colon (\boldsymbol{v_1},\dots, \boldsymbol{v_m})&\mapsto (\boldsymbol{w_1},\dots, \boldsymbol{w_n})A_g \end{aligned}
であることと,線形性から,
となる。したがって, g\circ f の表現行列は A_gA_f である。
証明終