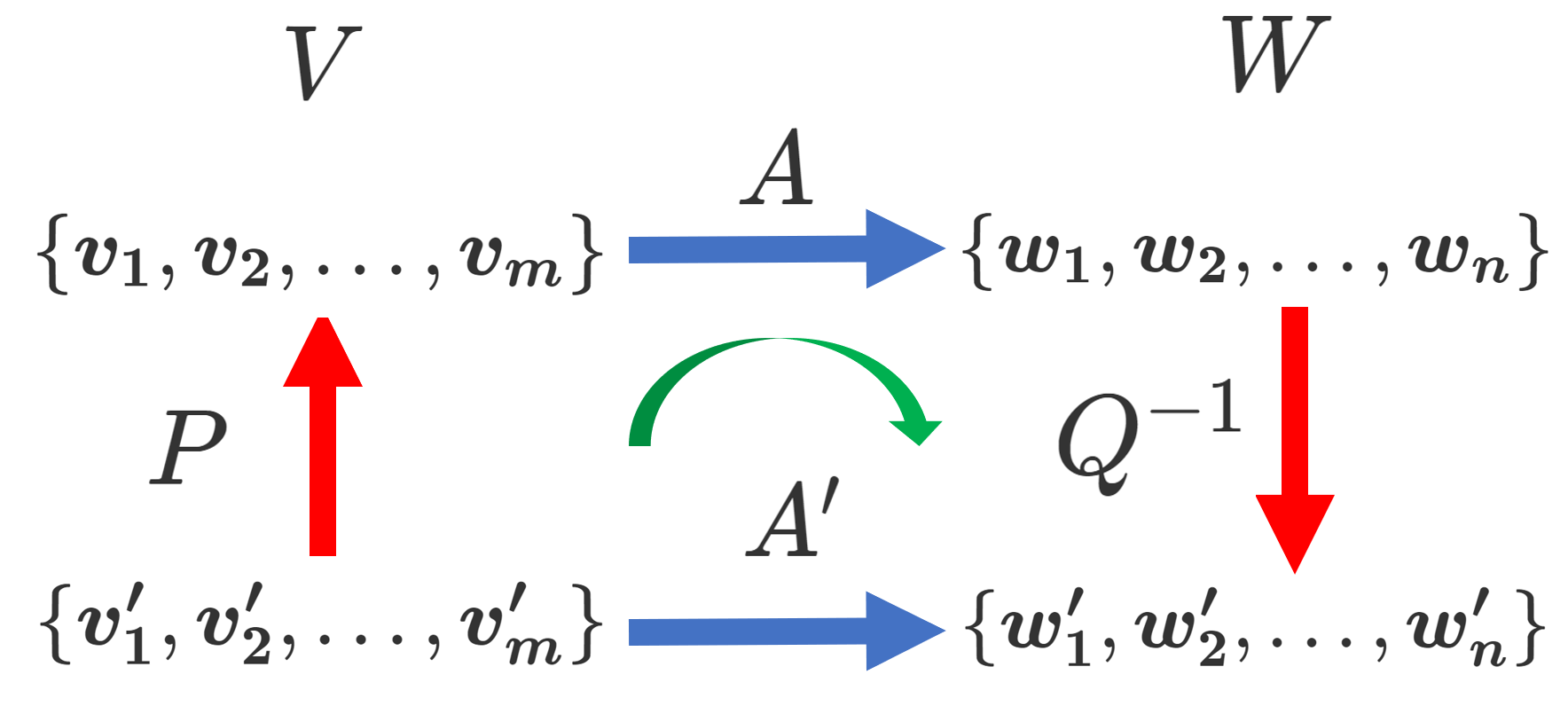
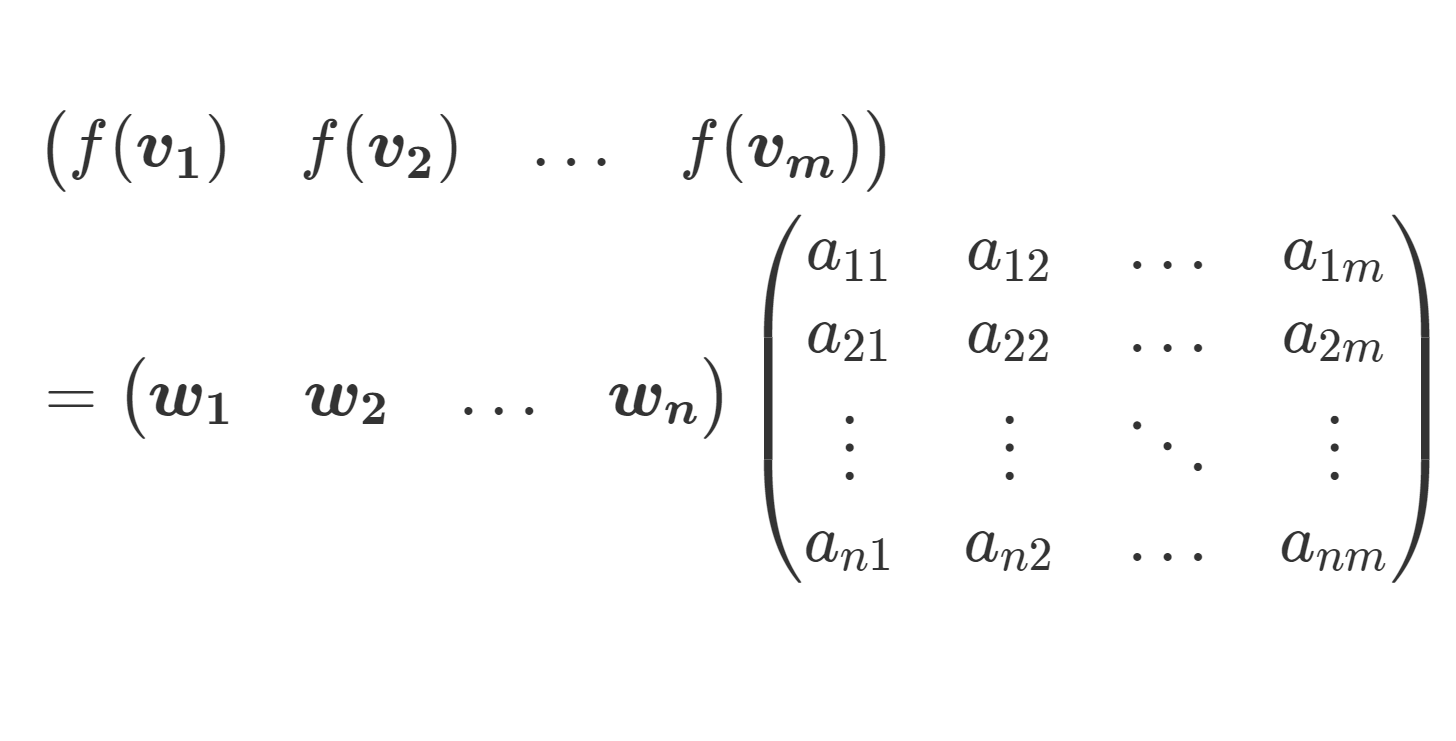行列の階数(ランク; rank)とは,それに対応する線形写像の像の次元であり,これは,行基本変形で階段行列に変形することで,求めることができます。
これについて,定義の詳細と,行基本変形で階段行列にする具体的な例題を紹介しましょう。
行列の階数(ランク)の定義
行列の階数(ランク; rank)は,同値な定義がたくさんあります。このうち,どれかが優位に「よく使われる」ということは,基本的にありません。どの定義もよく使うし,逆に行列のランクを求めるだけなら,一つの定義のみを覚えておけばよいです。
定義 (行列の階数(ランク; rank))
m\times n 行列 A に対し,以下の指標を A の階数 (ランク; rank)といい,\color{red} \operatorname{rank} A とかく。
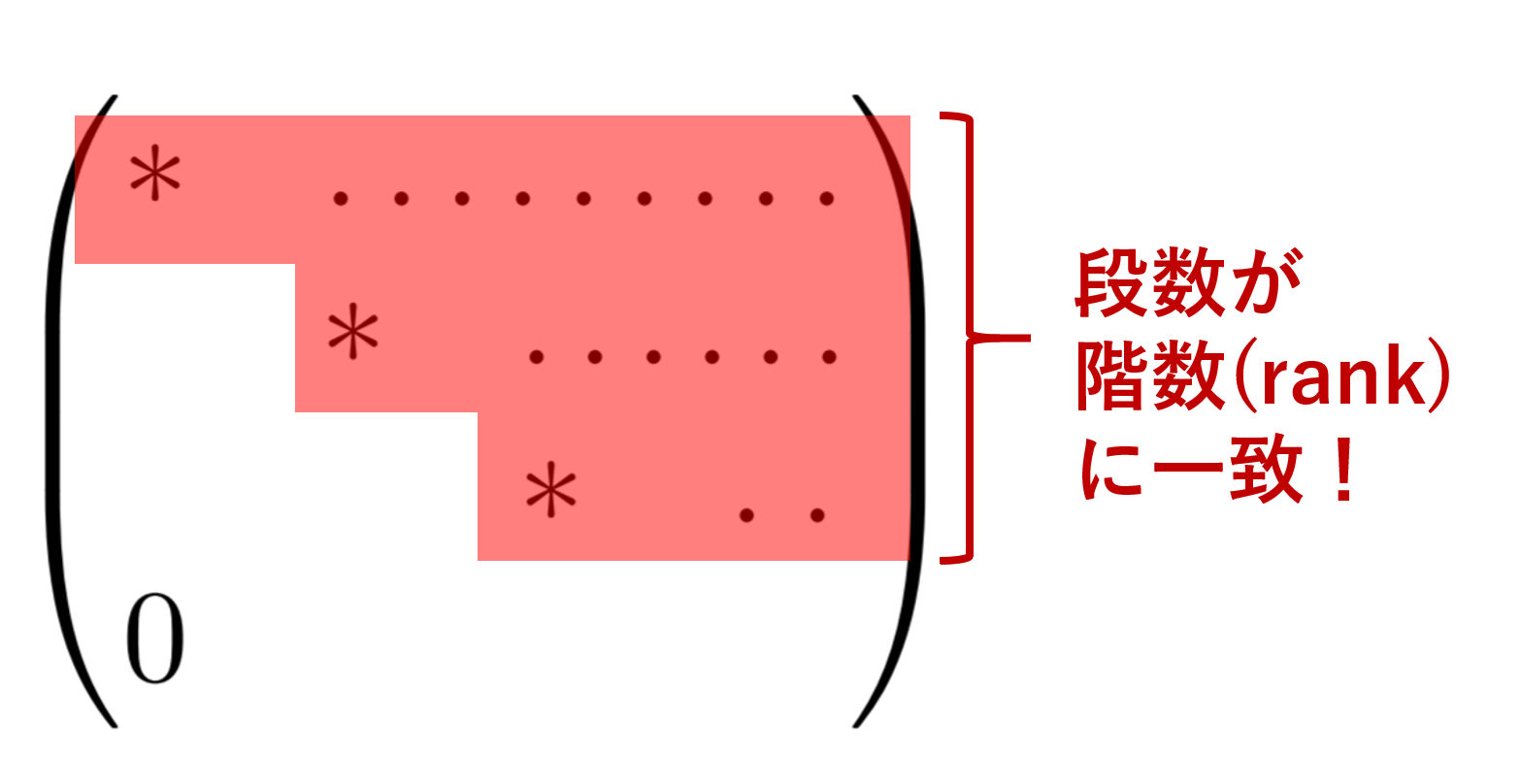
- A を行基本変形で階段行列に変形したときの 0 でない行の個数
- A の列ベクトルのうち,一次独立なベクトルの最大個数
- A の行ベクトルのうち,一次独立なベクトルの最大個数
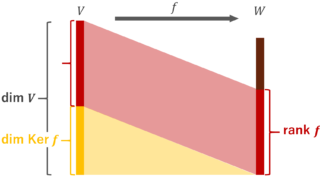
- A を線形写像 f の表現行列(行列表示)と思ったときの \operatorname{rank} f = \dim\operatorname{Im} f ,すなわち, f の像 (image) の次元 (これを,線形写像の階数(ランク; rank)という)。
- A の 0 でない特異値の数,すなわち AA^* の 0 でない固有値の数(重複度込み)。ただし, A^* は随伴行列(共役転置)を表す。
さまざまな定義があり,これらは全て同値ですが,その同値性の証明については,別の記事に預けることにしましょう。
定義から,m\times n 行列に対して,そのランクは \min\{m, n\} 以下になることが分かります。
今回,定義として採用するのは,1.にしましょう。これが一番階数(ランク)を求めるのには最適です。これを用いて,行列の階数(ランク)を求めましょう。
行列の階数(ランク)の求め方~計算の手順~
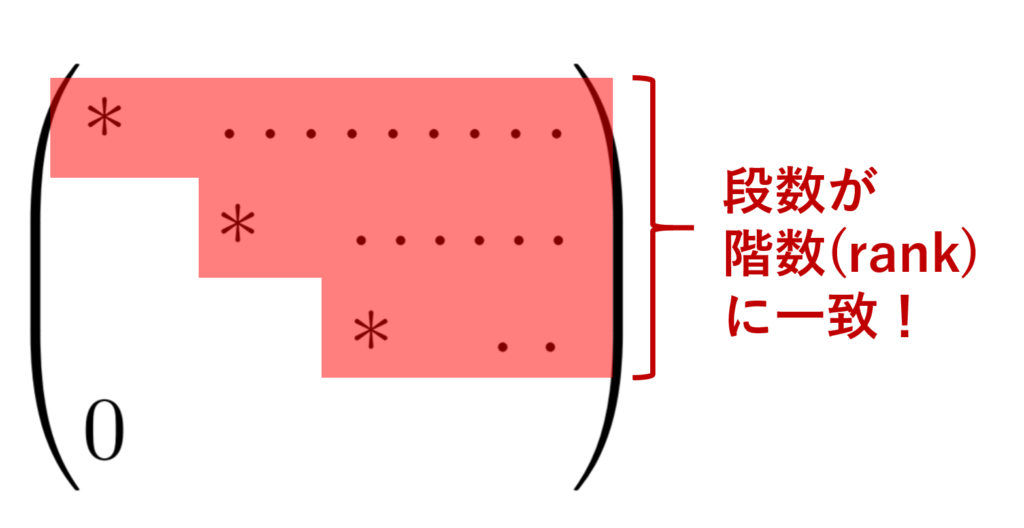
さて,行列の階数(ランク)の定義は,
1. A を行基本変形で階段行列に変形したときの 0 でない行の個数
でした。これについては,階段行列の作り方の話になりますから,まずは以下の記事を見るとよいでしょう。階段行列の作り方を詳細に解説しています。
上の記事の例題で,\begin{pmatrix} 1&1&3&5 \\ 2& 3& 7 & 8 \\ 1& 7& 0 & 0 \end{pmatrix} を階段行列に直していますね。それにより,この行列のランクは 3 と分かります。
これ以外に,もう一つ以下の問題を考えてみましょう。
例題
\begin{pmatrix}1 & 2 & 2 \\ 2 & 3 &4 \\ -1 & 1 & -2 \\ 3 & 0 & 6 \end{pmatrix} の階数(ランク)を求めよ。
行基本変形を復習しておくと,以下の3つの変形のことです。
- ある行の \boldsymbol{c} 倍を他の行に加えること
- 2つの行を入れ替えること
- ある行を \boldsymbol{ c \ne 0 } 倍すること
これを用いて,階段行列を作りましょう。すると,以下のようになります。実際,1.しか使っていませんね。
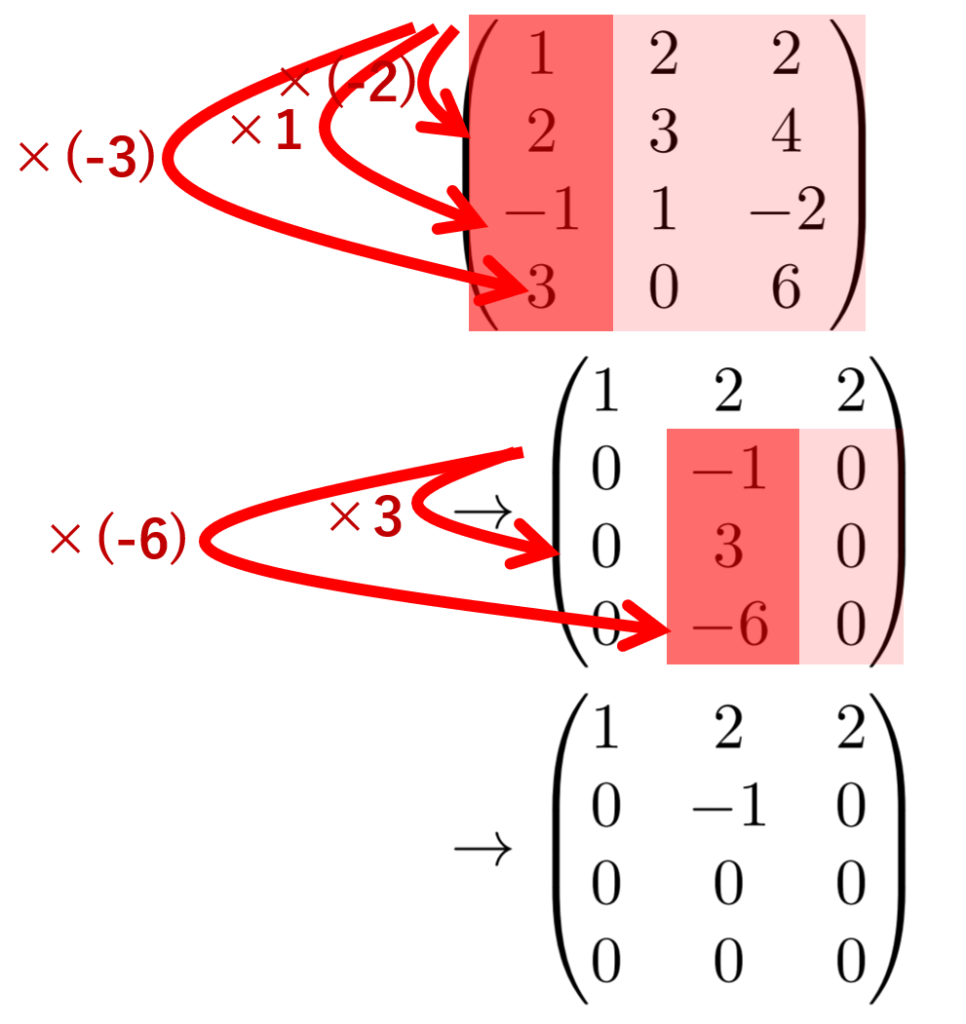
これで,階段行列が作れました。階段の 0 でない段数は 2 ですから,結局,
\operatorname{rank} \begin{pmatrix}1 & 2 & 2 \\ 2 & 3 &4 \\ -1 & 1 & -2 \\ 3 & 0 & 6 \end{pmatrix} = 2
が分かりましたね。