 数論
数論 ピタゴラス数の求め方(解)・性質とその証明
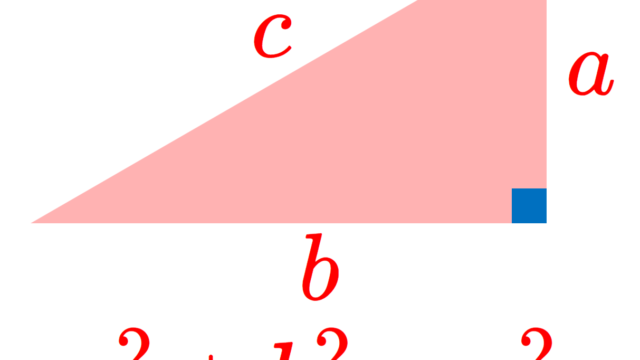
a^2+b^2=c^2をみたすような正の整数(a,b,c)をピタゴラス数といいます。特に,3数の最大公約数が1であるピタゴラス数(a,b,c)を原始ピタゴラス数といいます。原始ピタゴラス数は求め方があります。これについて掘り下げましょう。
 数論
数論 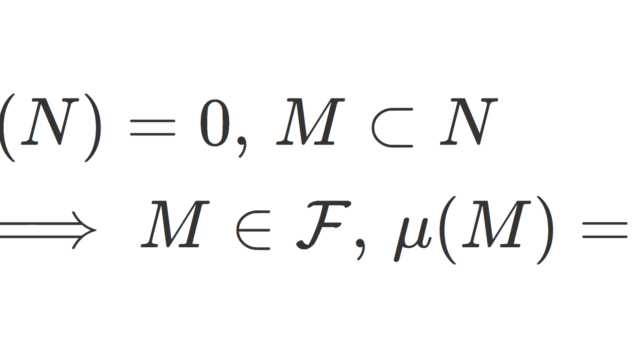 測度論
測度論  解析学(大学)その他
解析学(大学)その他  群・環・体
群・環・体 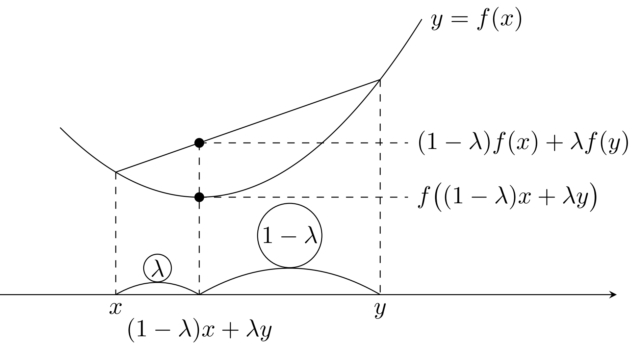 解析学(大学)その他
解析学(大学)その他 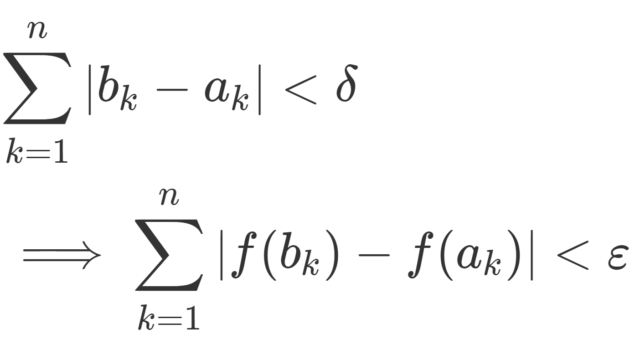 解析学(大学)その他
解析学(大学)その他 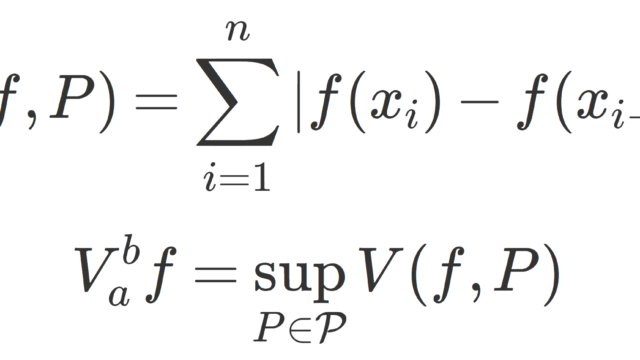 解析学(大学)その他
解析学(大学)その他 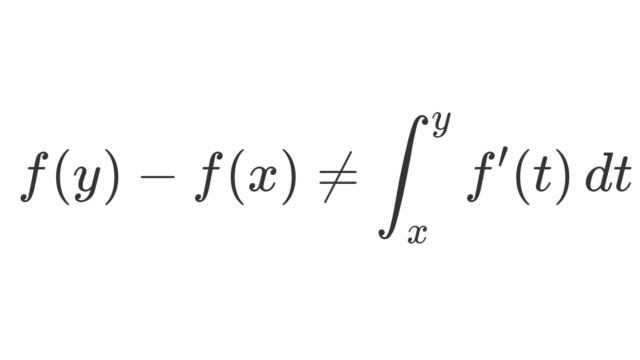 測度論
測度論 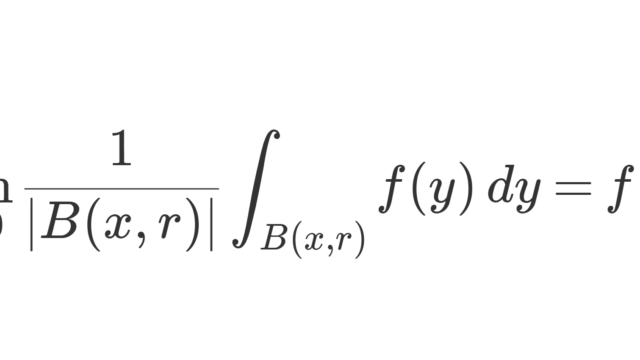 測度論
測度論 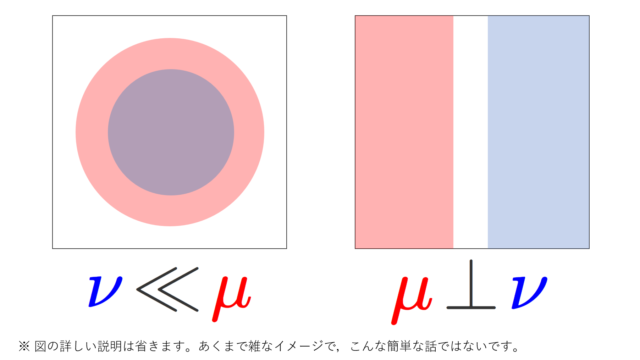 測度論
測度論