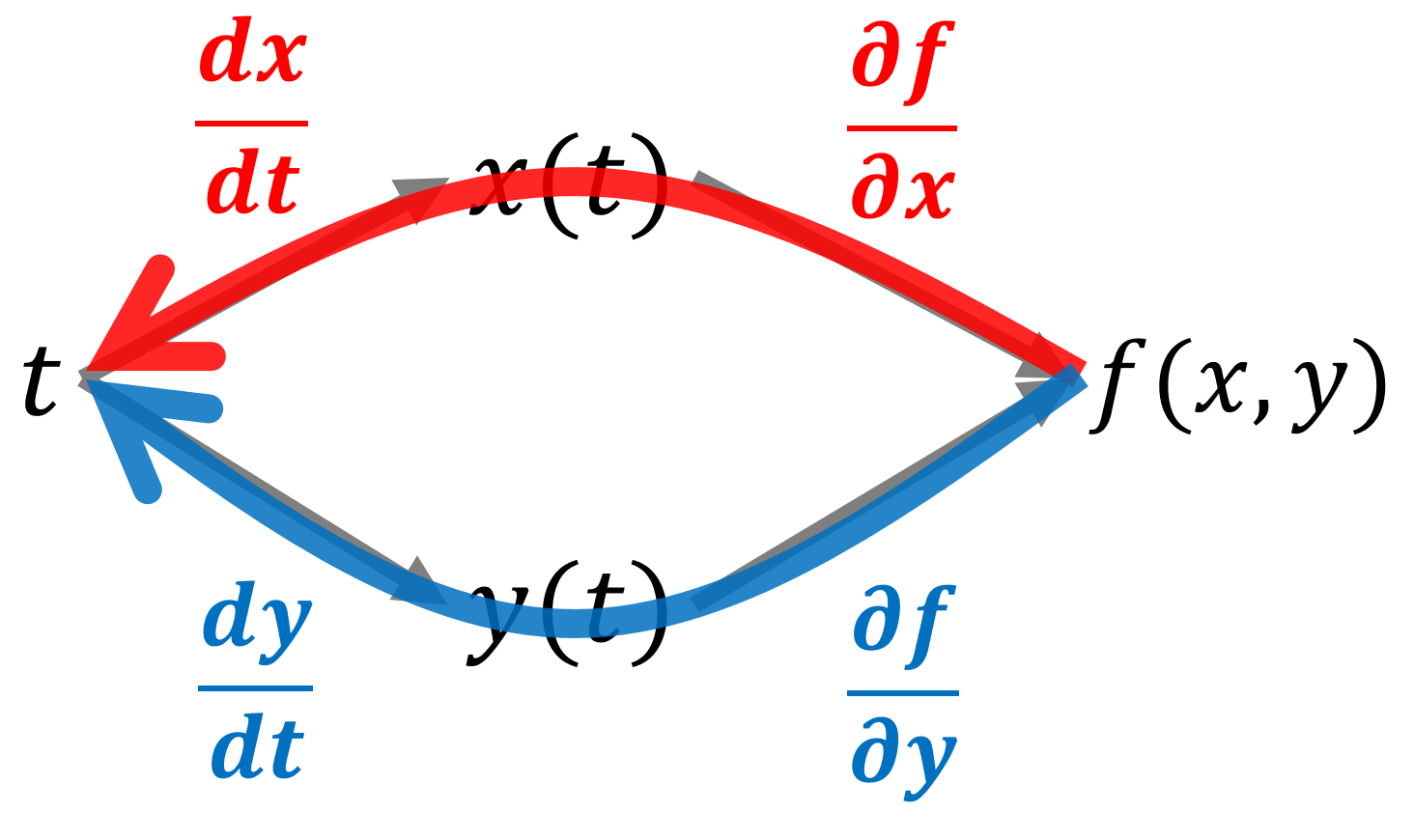
多変数の合成関数を偏微分する際の連鎖律(チェインルール)について,その覚え方と証明を行いましょう。
合成関数の偏微分における連鎖律(チェインルール)
まずは,代表的な2つの連鎖律を定理として述べることにしましょう。
関数の定義域,値域は明記しませんが, \mathbb{R}^2 や \mathbb{R} またはその部分集合で,合成関数がうまいこと定義できるようになっていると思ってください。
定理1(合成関数の偏微分における連鎖律1)
f(x,y) は C^1 級で, x=x(t),\; y=y(t) は微分可能とする。このとき,合成関数 t\mapsto f(x(t),y(t)) は微分可能で,
\color{red} \frac{df}{dt} = \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt}
が成り立つ。
本定理の証明は,一番最後にしましょう。赤字の等式は,
\begin{aligned} &\frac{df}{dt}(x(t),y(t))\\ &= \frac{\partial f}{\partial x}(x(t),y(t))\frac{dx}{dt}(t) + \frac{\partial f}{\partial y}(x(t),y(t))\frac{dy}{dt}(t)\end{aligned}
の意味です。
C^1 級とは,偏微分可能で全ての偏導関数が連続であることを指します(→C1級,Cn級,C∞級関数の定義と具体例5つ)。今回, f(x,y) を C^1 級にしましたが,より弱い「全微分可能」でも構いません。 C^1 級 \implies 全微分可能でしたね(→全微分の定義・性質・求め方を詳しく解説~全微分可能性~)。これは,次の定理でも同じです。
定理2(合成関数の偏微分における連鎖律2)
f(x,y) は C^1 級で, x=x(u,v),\; y=y(u,v) は偏微分可能とする。このとき,合成関数 (u,v)\mapsto f(x(u,v),y(u,v)) は偏微分可能で,
\color{red}\begin{aligned} \frac{\partial f}{\partial u} &= \frac{\partial f}{\partial x}\frac{\partial x}{\partial u} + \frac{\partial f}{\partial y}\frac{\partial y}{\partial u},\\ \frac{\partial f}{\partial v} &= \frac{\partial f}{\partial x}\frac{\partial x}{\partial v} + \frac{\partial f}{\partial y}\frac{\partial y}{\partial v} \end{aligned}
が成り立つ。
これは
\scriptsize \begin{aligned} &\frac{\partial f}{\partial u}(x(u,v),y(u,v)) \\&= \frac{\partial f}{\partial x}(x(u,v),y(u,v))\frac{\partial x}{\partial u}(u,v) + \frac{\partial f}{\partial y}(x(u,v),y(u,v))\frac{\partial y}{\partial u}(u,v) ,\\ &\frac{\partial f}{\partial v}(x(u,v),y(u,v)) \\&= \frac{\partial f}{\partial x}(x(u,v),y(u,v))\frac{\partial x}{\partial v}(u,v) + \frac{\partial f}{\partial y}(x(u,v),y(u,v))\frac{\partial y}{\partial v}(u,v) \end{aligned}
の意味です(サイズが小さくなってごめんなさい)。 u,v のうち,片方を固定してもう片方のみの変数と見れば,定理1からこの定理が従いますね。
合成関数の偏微分における連鎖律(チェインルール)の覚え方
連鎖律は,次のように考えて導きましょう。
- 変数の関係を図にする
- f から微分したい文字まで逆にたどる経路を考える
順番に解説していきます。
1. 変数の関係を図にする
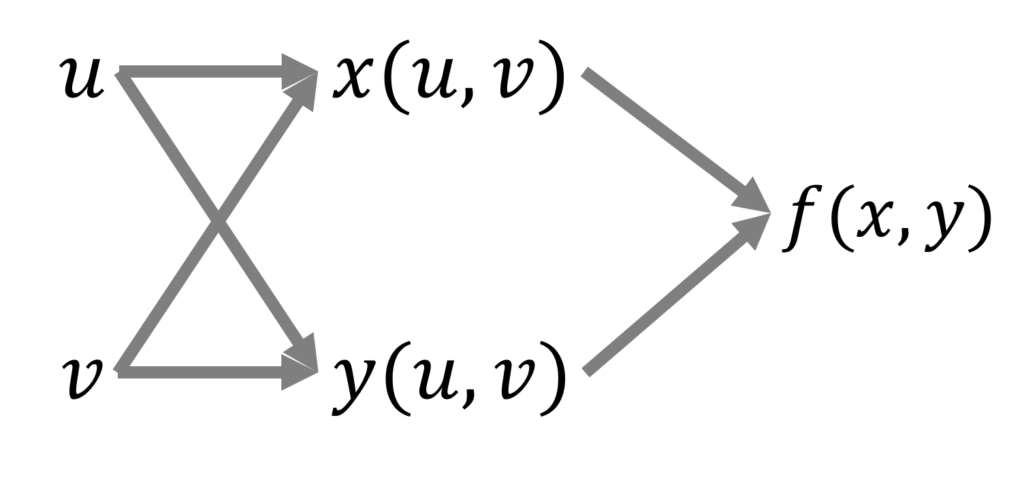
たとえば,合成関数 f(x(u,v), y(u,v)) の変数の関係を図にすると,以下のようになります。
2. fから微分したい文字まで逆にたどる経路を考える
上の図において, \partial f/\partial u を考えましょう。このとき, f から u まで戻る経路を考えます。そして,その経路に対応する微分を考えます。
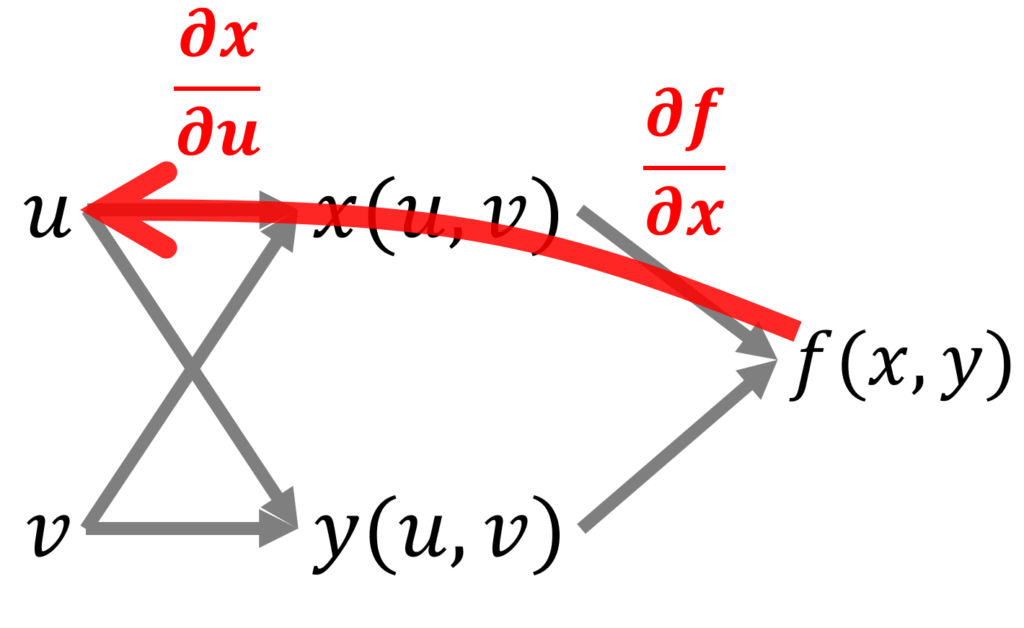
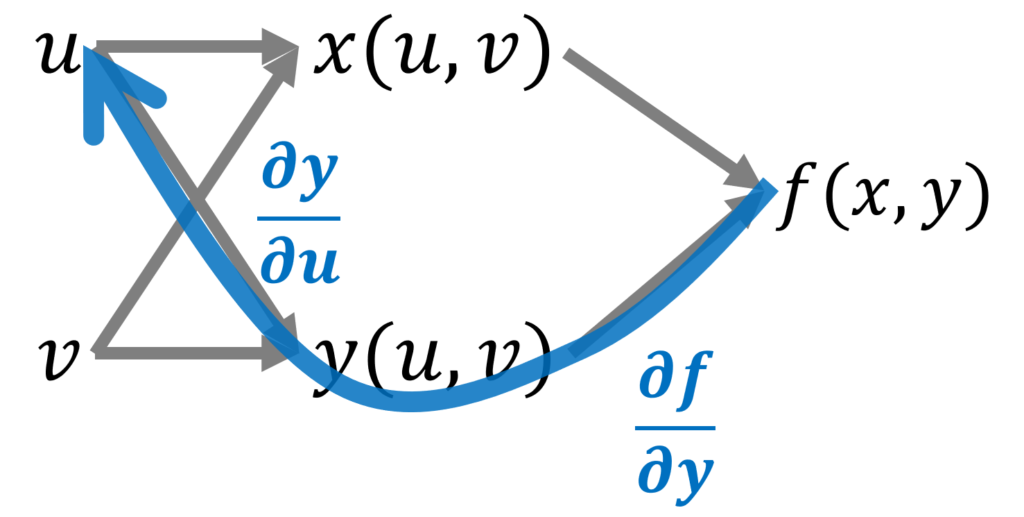
上の場合,2つ経路が見つかりました。これらの経路に対応する微分を足し合わせて,
\frac{\partial f}{\partial u} = \textcolor{red}{\frac{\partial f}{\partial x}\frac{\partial x}{\partial u}} + \textcolor{blue}{\frac{\partial f}{\partial y}\frac{\partial y}{\partial u}}
が答えになります。
これが,連鎖律(チェインルール)の導出方法です。
この方法を用いればどんな場合でも対応可能!
この方法を用いれば,どんな場合でも対応可能です。たとえば, f(x(t), y(t)) について, df/dt は以下のようになります。
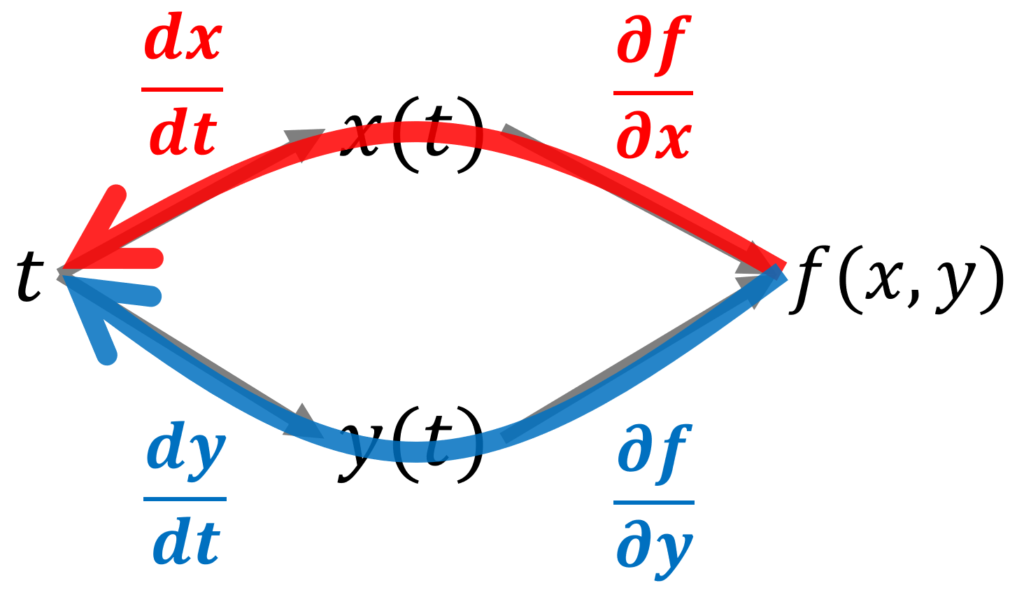
このことから,
\frac{df}{dt} = \textcolor{red}{\frac{\partial f}{\partial x}\frac{dx}{dt}} + \textcolor{blue}{\frac{\partial f}{\partial y}\frac{dy}{dt}}
が導けるわけです。他に,もう少し難しい例を考えましょう。たとえば, f(x(u, v), y(u, v), z(u, v)) において, \partial f/\partial u を求めたい場合も,以下の図を考えて,
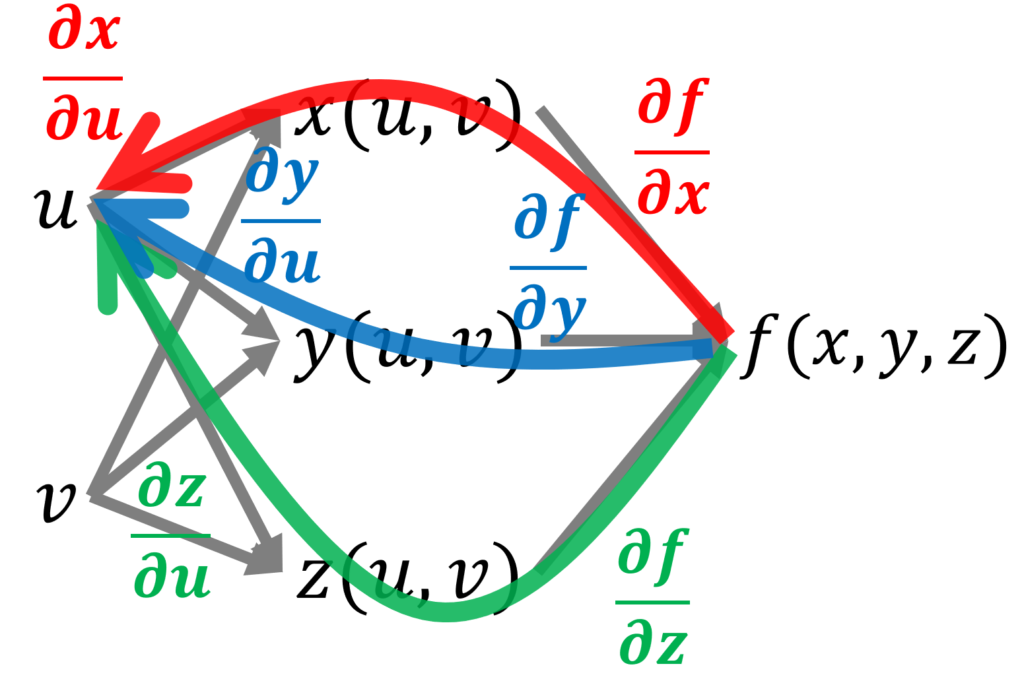
が導けます。
さらに,もう一段深い合成関数でも同じです。たとえば, f(x(u(t), v(t)), y(u(t), v(t))) について, df/dt を考えたい場合は,以下から,
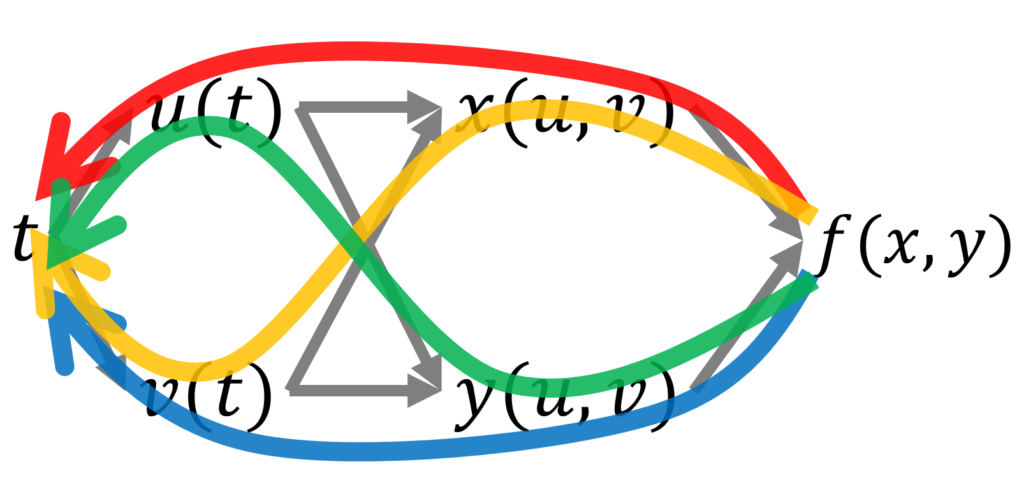
が求まります。
なお,ヤコビ行列が分かるのであれば,合成関数の偏微分は,単に J(g\circ f(x)) = Jg(f(x)) Jf(x) と思ってもよいかもしれません。
合成関数の偏微分における連鎖律(チェインルール)の証明
定理1のみ証明しておきましょう。定理1を再掲します。
定理1再掲(合成関数の偏微分における連鎖律1)
f(x,y) は C^1 級で, x=x(t),\; y=y(t) は微分可能とする。このとき,合成関数 t\mapsto f(x(t),y(t)) は微分可能で,
\color{red} \frac{df}{dt} = \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt}
が成り立つ。
証明
f が全微分可能であるとして証明する。全微分可能性より,
\begin{aligned}&\frac{f(x(t+h), y(t+h))- f(x(t), y(t))}{h}\\ &=f_x(x(t), y(t))\frac{x(t+h)-x(t)}{h}\\&\qquad + f_y(x(t), y(t))\frac{y(t+h)-y(t)}{h}\\ &\qquad\qquad+ \frac{o(h)}{h}\\ &\xrightarrow{h\to 0} f_x(x(t),y(t)) x'(t)+f_y(x(t),y(t))y'(t) \end{aligned}
より,題意は示された。途中,ランダウの記号 o を用いた。
証明終
合成関数の微分の証明では, 0 での割り算が問題になることがありますが,今回は全微分の定義を使っているだけので,その心配はありません。