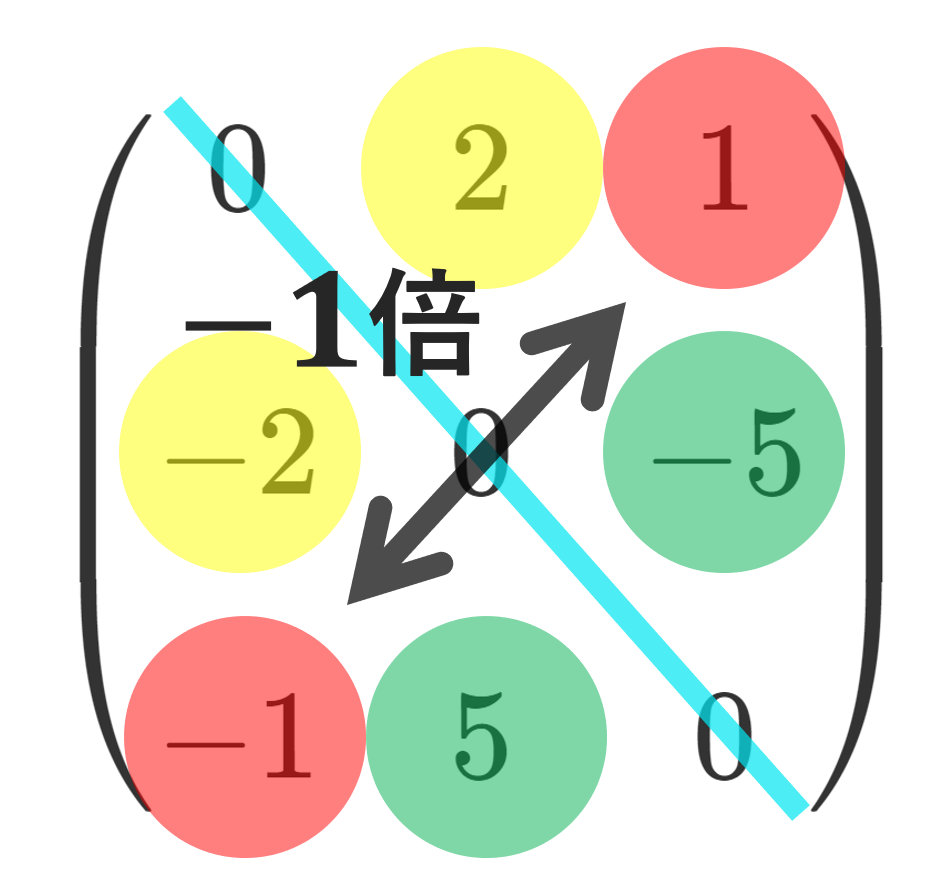
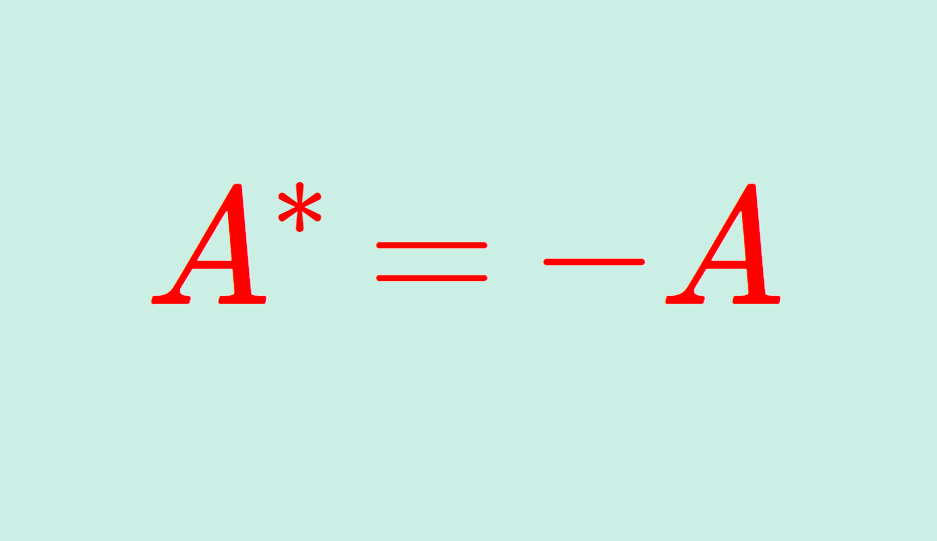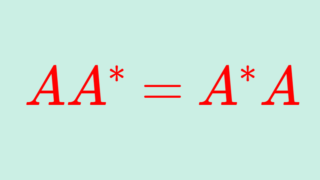歪エルミート行列(わいえるみーとぎょうれつ,反エルミート行列)とは,随伴行列(共役転置)をとると元の行列の -1 倍になるような行列を指します。すなわち, A^*=-A ですね。
これについて,その定義と性質を解説しましょう。
歪エルミート行列の定義
定義(歪エルミート行列)
A を正方行列とする。
\Large \color{red}A^* = -A
をみたすとき,A を歪エルミート行列 (反エルミート行列; Skew-Hermitian matrix) という。ただし, A^* = \overline{A}^\top は随伴行列(共役転置)を指します。
歪エルミート行列は「わいえるみーとぎょうれつ」と読みます。定義は, \color{red} \overline{A}=-A^\top としても同じです。
実数における交代行列の複素数版だといえます。交代行列については,交代行列の定義と重要な性質5つで解説しています。
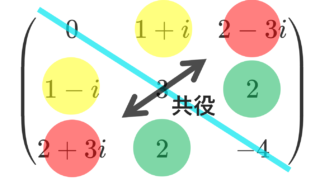
軽く具体例を挙げておきましょう。
歪エルミート行列の具体例
歪エルミート行列の重要な性質5つ
定理(歪エルミート行列の性質)
- A を正方行列とするとき, \color{red} A-A^* は歪エルミート行列である。
- 歪エルミート行列の対角成分は純虚数または 0 である。
- A を歪エルミート行列とするとき,iA はエルミート行列である。
- A を n 次歪エルミート行列, \boldsymbol{x},\boldsymbol{y}\in\mathbb{C}^n を列ベクトルとする。このとき,内積について \color{red} \langle A\boldsymbol{x},\boldsymbol{y}\rangle =-\langle \boldsymbol{x},A\boldsymbol{y}\rangle が成り立つ。
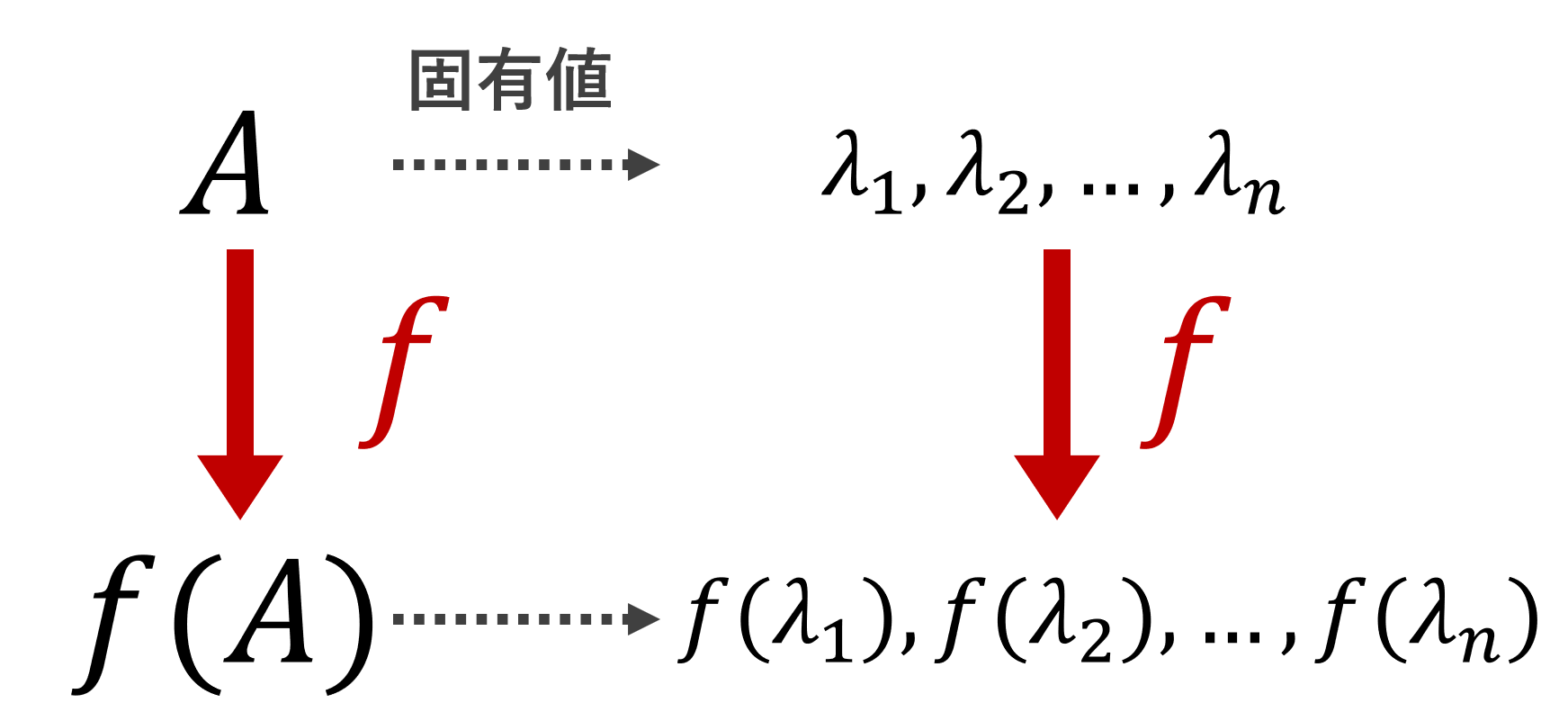
- 歪エルミート行列の固有値は純虚数または 0 である。
なお,歪エルミート行列は AA^* = -A^2 = A^*A ですから,正規行列です。よって,歪エルミート行列は正規行列の性質もみたします。たとえば,歪エルミート行列は対角化可能です。正規行列の性質については,以下で解説しています。
1. A-A^*は歪エルミート行列であること
証明
(A-A^*)^* = A^* -(A^*)^* = -(A-A^*)
より, A-A^* は歪エルミート行列となる。
証明終
任意の正方行列 A に対して,
A=\frac{1}{2}(A+A^*)+\frac{1}{2}(A-A^*)
であり, (A+A^*)/2, (A-A^*)/2 はそれぞれエルミート行列・歪エルミート行列ですから,任意の行列はエルミート行列と歪エルミート行列の和に分解できることになります。
2. 歪エルミート行列の対角成分は純虚数または0であること
証明
A=(a_{ij}) を歪エルミート行列とする。 A^*=-A より, \overline{a}_{ii} = -a_{ii}. これは a_{ii} は純虚数または 0 であることを意味する。
証明終
3. A が歪エルミート行列なら iA がエルミート行列であること
エルミート行列とは, A^*=A をみたす行列です(→エルミート行列の定義と性質4つとその証明)。
証明
A を歪エルミート行列とすると,
(iA)^* = \overline{iA^\top} = -i\, \overline{A^\top}=-iA^*=iA
より,iA はエルミート行列である。
証明終
4. <Ax,y> = -<x,Ay> であること
証明
一般に正方行列 A について,\langle A\boldsymbol{x},\boldsymbol{y}\rangle = \langle \boldsymbol{x}, A^*\boldsymbol{y}\rangle であることに注意する(→随伴行列(エルミート転置,共役転置)の定義と性質10個)。
今の場合, A^*= -A なので,
\langle A\boldsymbol{x},\boldsymbol{y}\rangle = \langle \boldsymbol{x},-A\boldsymbol{y}\rangle =- \langle \boldsymbol{x},A\boldsymbol{y}\rangle.証明終
5. 歪エルミート行列の固有値は純虚数または0であること
証明
\lambda\in\mathbb{C} を実交代行列 A の固有値とし,\boldsymbol{x} をそれに対応する列ベクトルとする。このとき, A\boldsymbol{x}=\lambda \boldsymbol{x} である。性質4.より, \langle A\boldsymbol{x},\boldsymbol{x}\rangle = -\langle \boldsymbol{x},A\boldsymbol{x}\rangle が成立するので。
\langle \lambda \boldsymbol{x},\boldsymbol{x}\rangle =- \langle \boldsymbol{x}, \lambda\boldsymbol{x}\rangle .
すなわち, \langle \lambda \boldsymbol{x},\boldsymbol{x}\rangle =-\overline{\lambda} \langle \boldsymbol{x}, \boldsymbol{x}\rangle,すなわち (\lambda+\overline{\lambda})\lVert \boldsymbol{x}\rVert^2=0 なので, \lambda+\overline{\lambda} =0. これは \lambda は純虚数または 0 である。
証明終
途中で用いたのは内積の共線形性ですね。 \langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle = \lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle ,\; \langle \boldsymbol{x}, \lambda\boldsymbol{x}\rangle =\overline{ \langle \lambda \boldsymbol{x}, \boldsymbol{x}\rangle }=\overline{ \lambda \langle \boldsymbol{x}, \boldsymbol{x}\rangle }=\overline{\lambda} \langle \boldsymbol{x}, \boldsymbol{x}\rangle です。