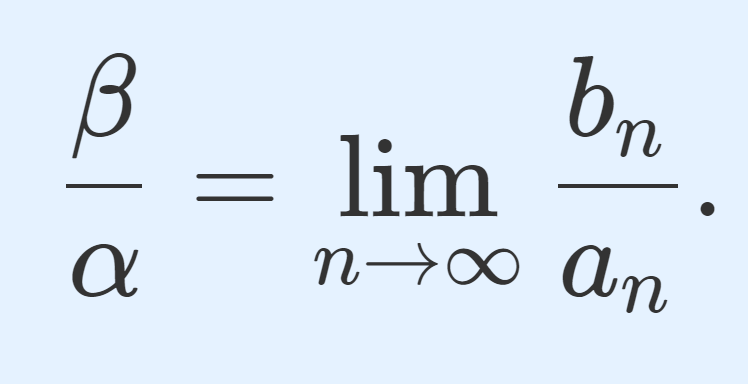数学における「追い出しの原理」といわれるものについて，その定理と，大学で習うイプシロンエヌ論法・イプシロンデルタ論法を用いた証明を行います。
数列版の追い出しの原理
まずは数列版について述べます。
数列版の定理の主張
定理（追い出しの原理；数列版）
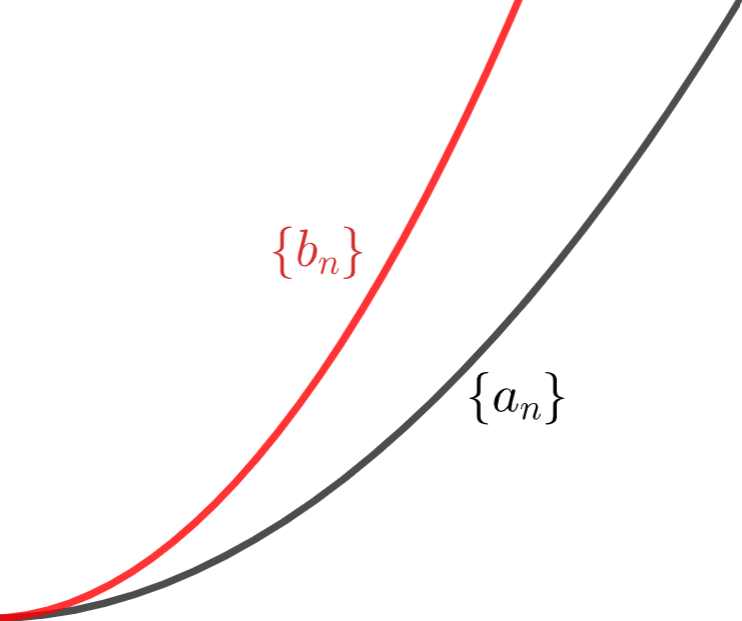
実数の数列 \{b_n\}, \{a_n\} が，
\color{red} a_n \le b_n \,\,(n\ge 1 ) かつ \color{red} \displaystyle\lim_{n\to\infty} a_n =\infty となるとする。
このとき，
が成立する。
同様に，a_n \ge b_n,\,\, \lim_{n\to\infty} a_n = -\infty \implies \lim_{n\to\infty} b_n = -\infty も従います。
早速証明しましょう。
数列版の証明
証明にはイプシロンエヌ論法を使います。これを理解していれば非常に簡単です。（→ イプシロンエヌ論法をわかりやすく丁寧に～数列の極限の定義～）
収束先が \infty の方のみ証明しましょう。 - \infty のときは， a_n を -a_n に置き換えれば同様です。
証明
K > 0 とする。 \lim_{n\to\infty} a_n = \infty であるから，ある N \ge 1 が存在して，
n \ge N \implies a_n > K
となる。このとき， b_n \ge a_n > K であるから，
も成立する。これは， \lim_{n\to\infty} b_n = \infty を意味する。
証明終
関数版の追い出しの原理
つづいて関数版についても述べましょう。
関数版の定理の主張
定理（追い出しの原理；関数版）
f,g を -\infty \le a\le \infty の周りで定義されている実数値関数とし，
\displaystyle \color{red} f(x) \le g(x), \,\, \lim_{x\to a} f(x) =\infty であるとする。
このとき，
が成立する。
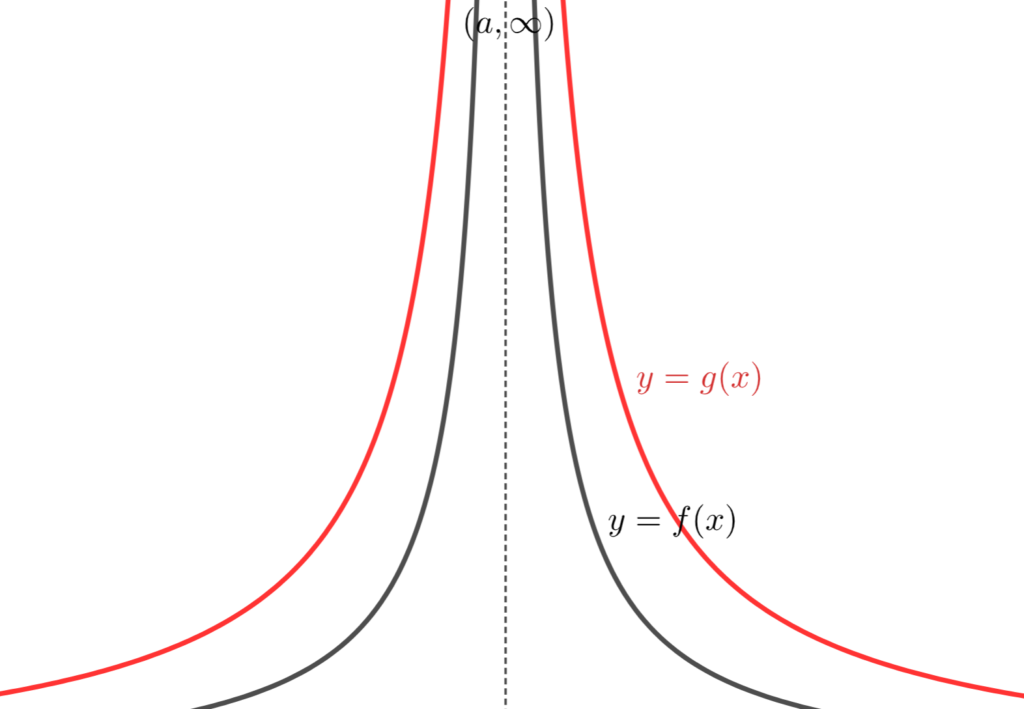
同様に， f(x) \ge g(x),\,\, \lim_{x\to a} f(x) = -\infty \implies \lim_{x\to a} g(x) = - \infty も従います。
関数版の証明
証明にはイプシロンデルタ論法を用います。これを理解していれば，こちらも簡単です。（→ イプシロンデルタ論法をわかりやすく丁寧に～関数の極限の定義～）
-\infty < a < \infty のときのみ証明しましょう。 a = \pm\infty のときは数列のときと同様です。
証明
K > 0 とする。 \lim_{x\to a} f(x) = \infty より，ある \delta> 0 が存在して，
|x-a| < \delta \implies f(x) > K
となる。ここで， g(x) \le f(x) > K であるから，
も成り立つ。これは \lim_{x\to a} g(x) =\infty を意味する。
証明終
似たような定理～はさみうちの原理～
同様のものに，はさみうちの原理というものがあります。主張のみ述べましょう。
数列版の定理の主張
定理（はさみうちの原理；数列版）
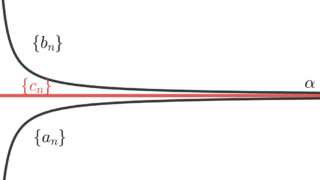
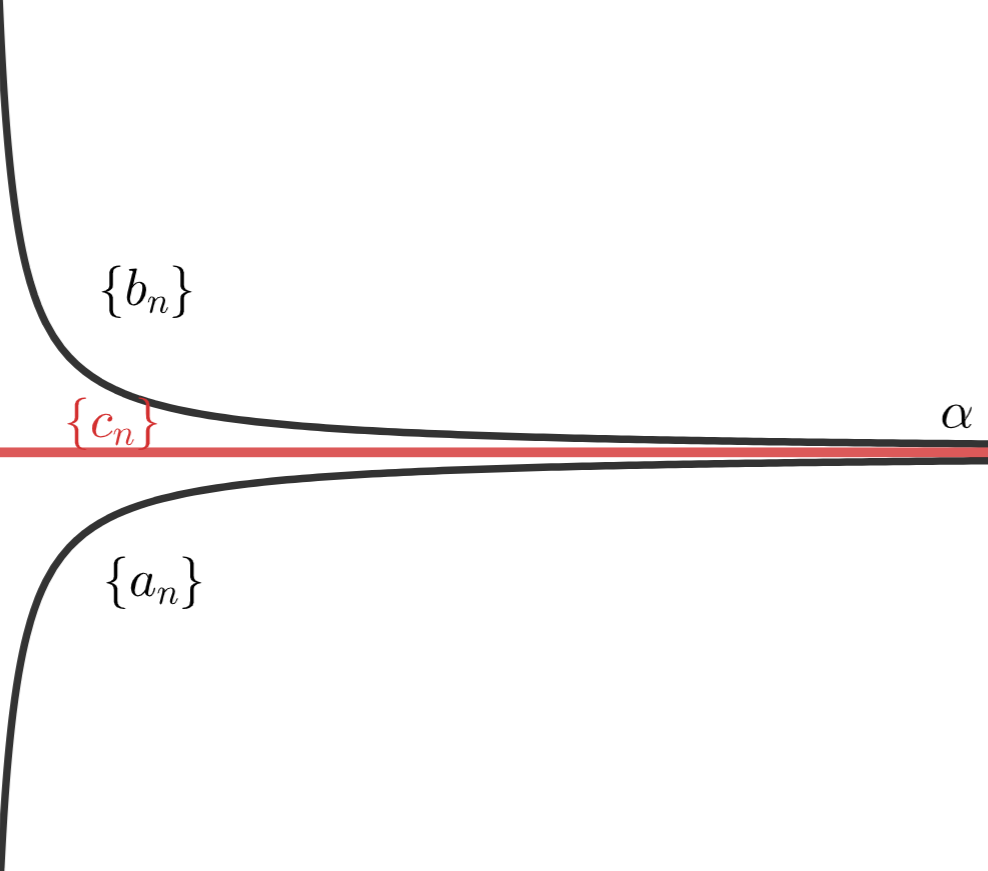
実数の数列 \{a_n\}, \{b_n\}, \{c_n\} において，
\color{red} a_n \le c_n \le b_n \,\, (n \ge 1 ) かつ \displaystyle \color{red}\lim_{n\to\infty} a_n = \lim_{n\to\infty} b_n = \alpha \in\mathbb{R} とする。
このとき，
が成立する。
関数版の定理の主張
定理（はさみうちの原理；関数版）
f,g,h を -\infty \le a\le \infty の周りで定義されている実数値関数とし，
\displaystyle \color{red} f(x) \le h(x) \le g(x), \,\, \lim_{x\to a} f(x) = \lim_{x\to a} g(x) = b \in\mathbb{R} であるとする。
このとき，
が成立する。
これの証明は，以下を参照してください。
