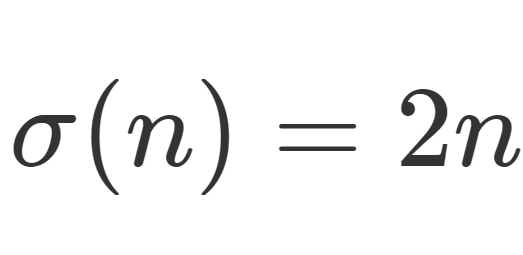 数論
数論 完全数の定義と性質とその証明
完全数 (perfect number) とは,自分以外の正の約数の総和が自分自身に一致する数のことです。たとえば,28=1+2+4+7+14は完全数です。完全数について,その定義とメルセンヌ素数を絡めた性質を紹介しましょう。
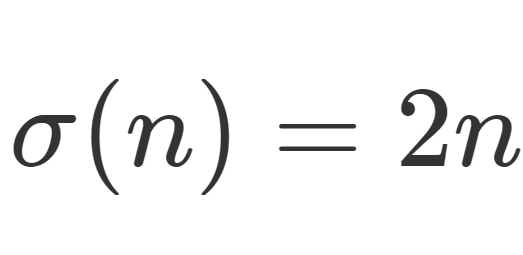 数論
数論 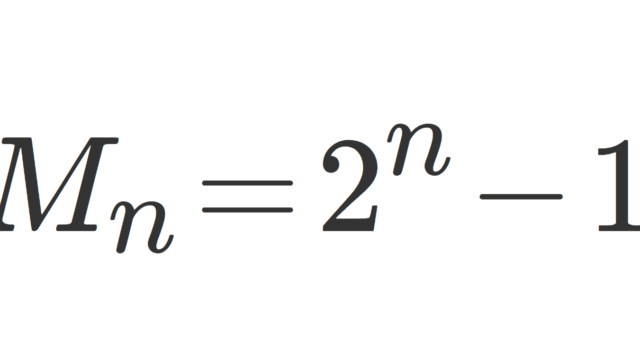 数論
数論  測度論
測度論 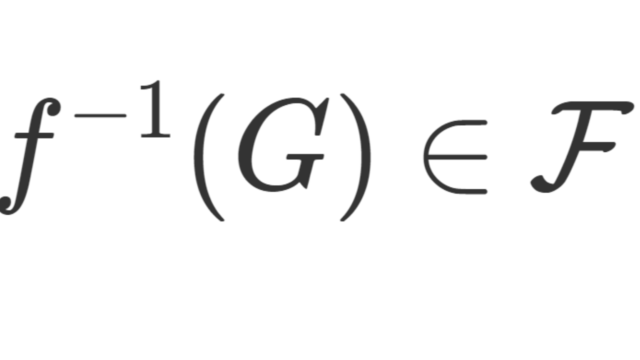 測度論
測度論 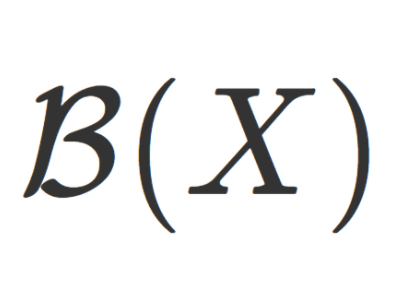 測度論
測度論 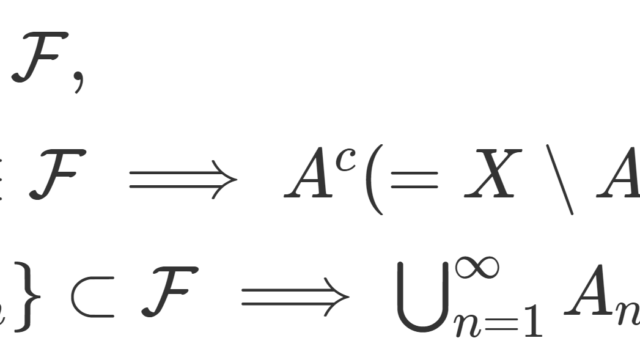 測度論
測度論 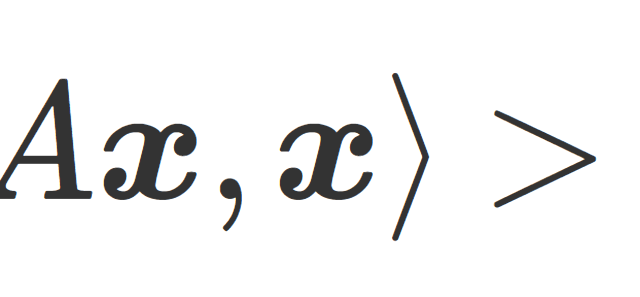 線形代数学
線形代数学 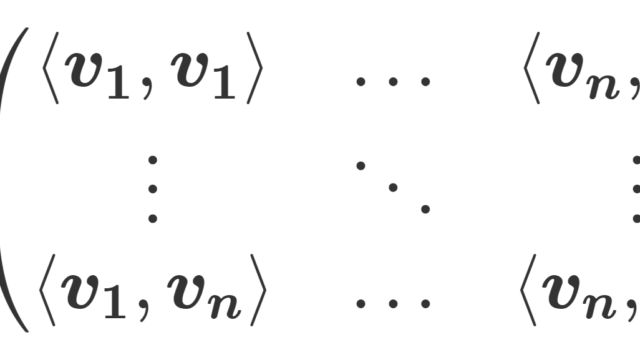 線形代数学
線形代数学 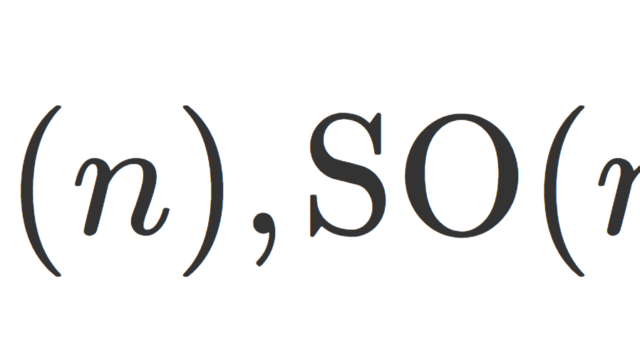 群・環・体
群・環・体 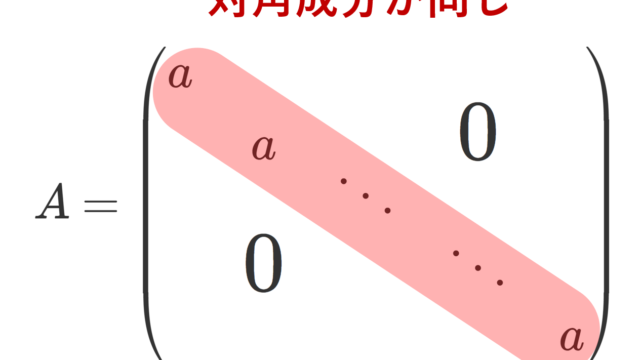 線形代数学
線形代数学