 解析学(大学)その他
解析学(大学)その他 【トマエ関数】無理数で連続,有理数で不連続な関数
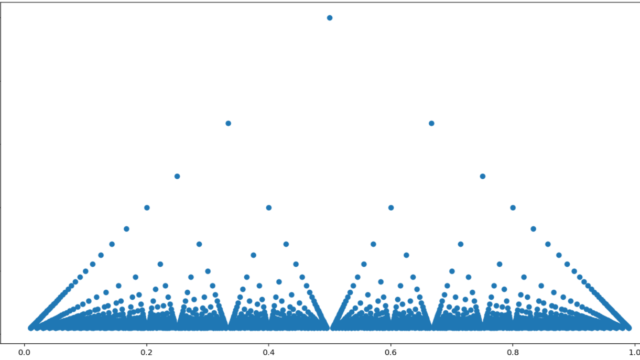
有理数で分母分の1,無理数で0となる関数をトマエ関数 (Thomae function) と言います。この関数について,その定義と性質2つ(無理数で連続,有理数で不連続,リーマン積分可能性)を紹介しましょう。
 解析学(大学)その他
解析学(大学)その他 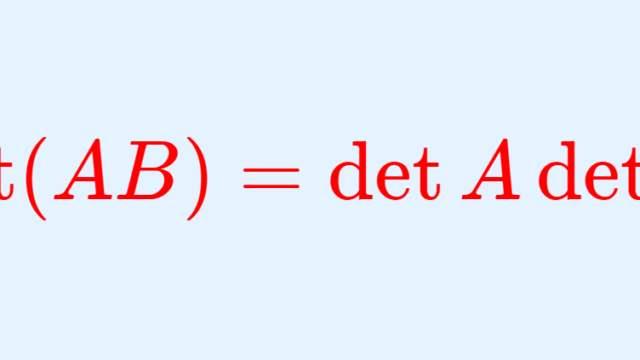 線形代数学
線形代数学  微分積分学(大学)
微分積分学(大学)  線形代数学
線形代数学 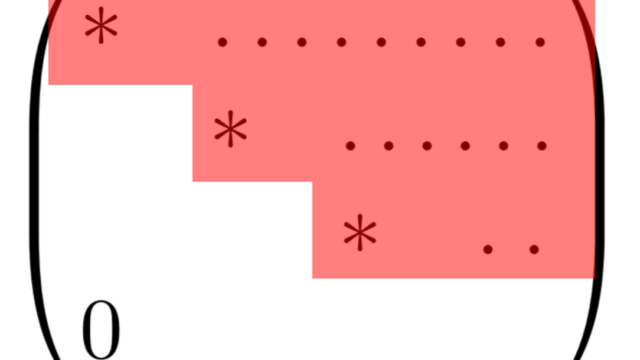 線形代数学
線形代数学 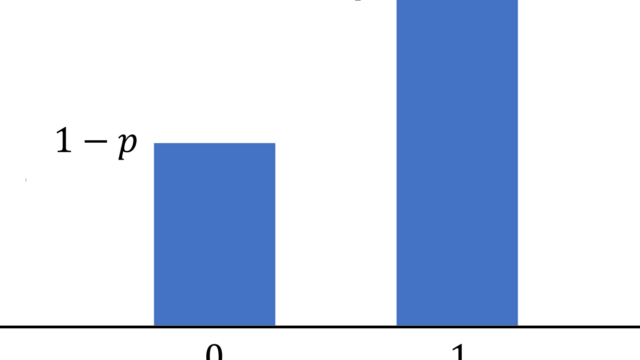 確率論
確率論 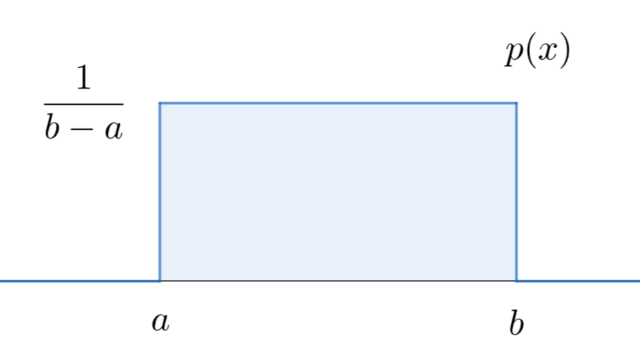 確率論
確率論 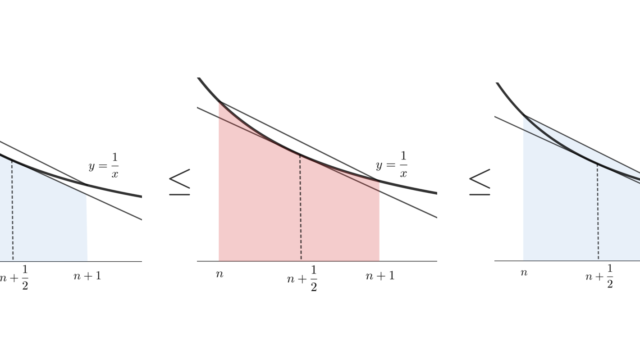 微分積分学(大学)
微分積分学(大学) 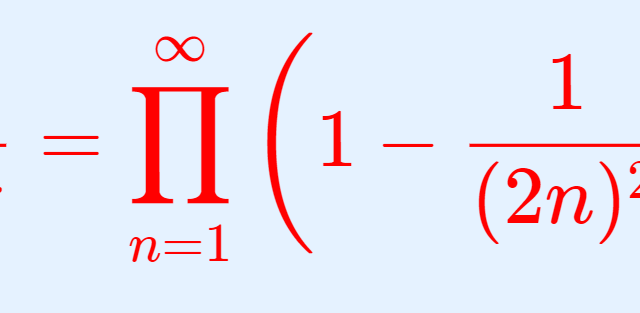 微分積分学(大学)
微分積分学(大学) 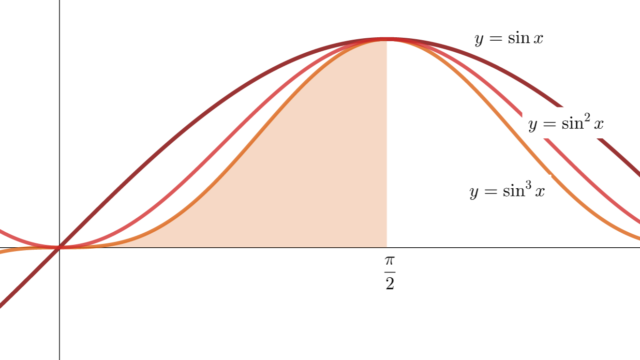 微分積分学(大学)
微分積分学(大学)