 集合と位相
集合と位相 相対コンパクトの定義と例と性質
相対コンパクトとは,閉包がコンパクトになるような部分集合のことを言います。相対コンパクトについて,その定義と具体例,さらにはネット(有向点族)・点列との関係性まで紹介しましょう。
 集合と位相
集合と位相 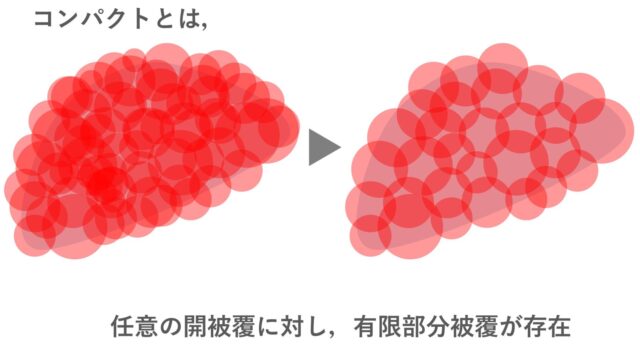 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相