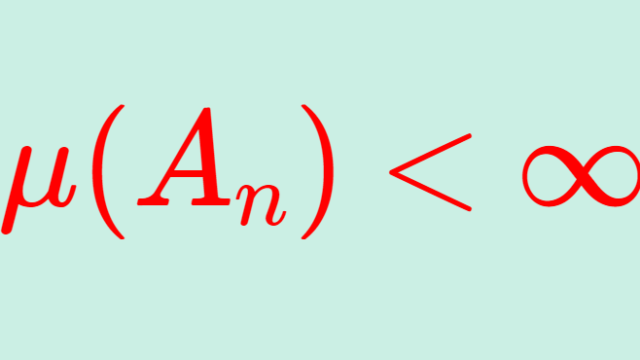 測度論
測度論 σ有限な測度とは~定義と例・反例~
σ-有限測度 (σ-finite) とは,μ(A_n)<∞ (n≧1) かつ A_n ↑ X となる可測集合列 {A_n} が取れることを言います。σ-有限測度について,定義と具体例を挙げましょう。
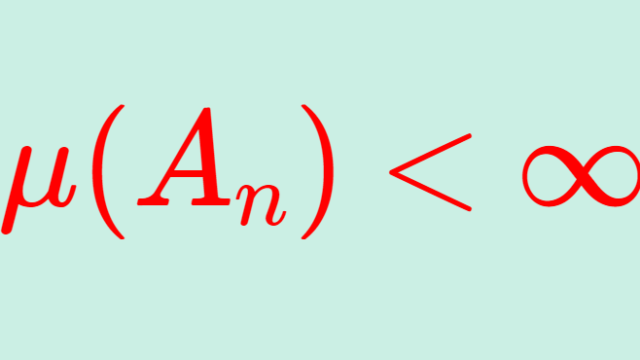 測度論
測度論 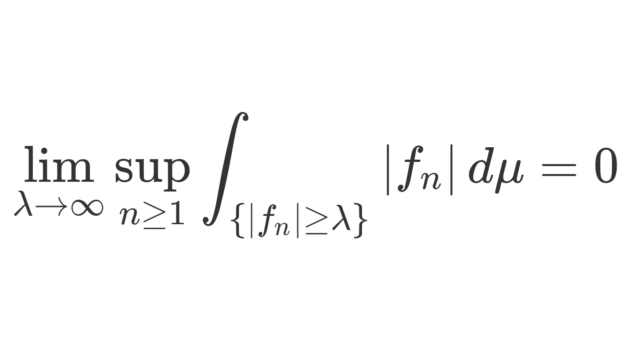 測度論
測度論 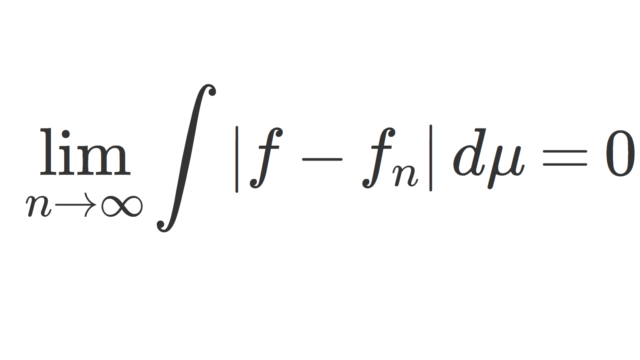 測度論
測度論 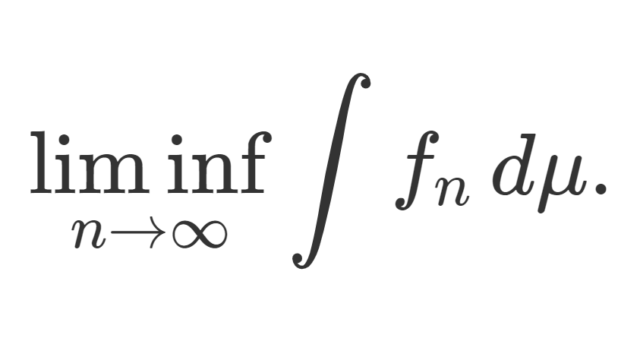 測度論
測度論 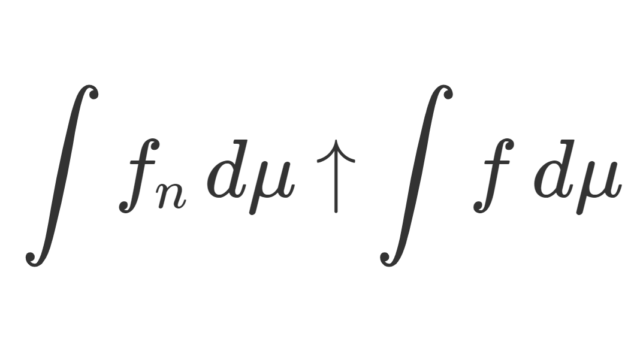 測度論
測度論 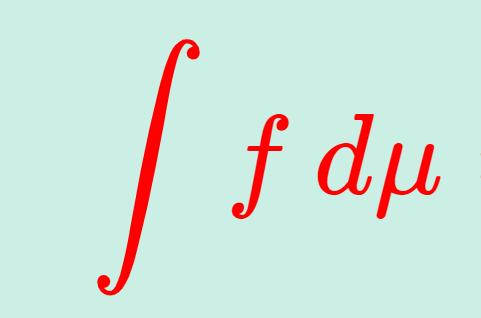 測度論
測度論  群・環・体
群・環・体 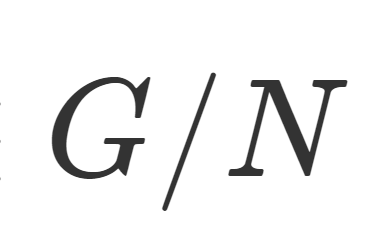 群・環・体
群・環・体 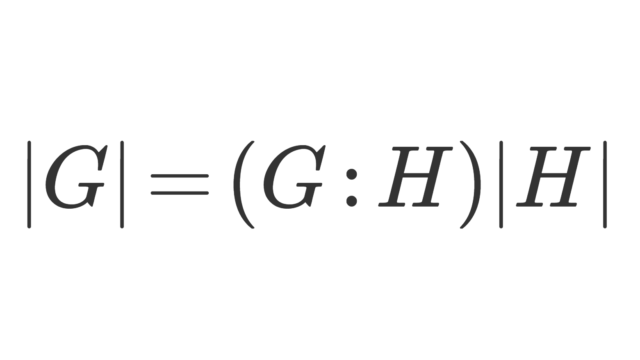 群・環・体
群・環・体 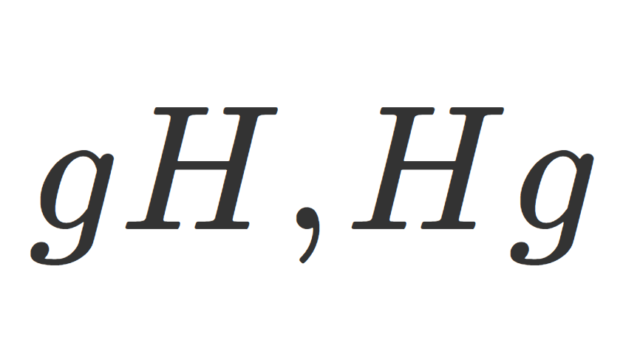 群・環・体
群・環・体