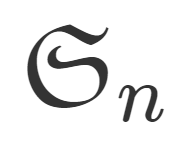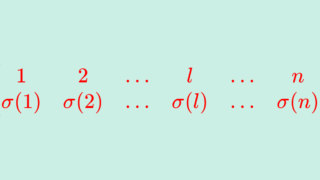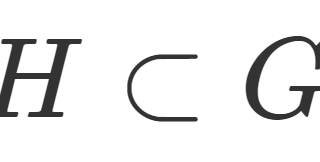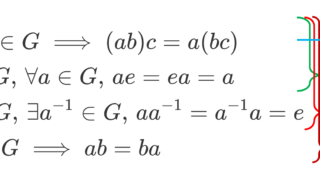対称群・交代群はそれぞれ置換・偶置換を集めた集合を表します。「置換・偶置換」とは,行列式の定義にも用いたやつです(→行列式の性質6つの証明(列,行の線形性,置換,積,転置など))。
これについて,詳しい定義や性質を解説しましょう。
【置換群】対称群・交代群とは
本記事では,置換のある程度の知識を仮定します。随所で復習を入れますが,もし全く知らないのであれば,以下の記事を読んでからの方が良いでしょう。
さて,対称群・交代群・置換群の定義を紹介しましょう。
対称群・置換群の定義
対称群・置換群の定義のために,まずは「置換」の復習をしましょう。
全単射 \sigma\colon \{1,2,3,\dots, n\} \to \{1,2,3,\dots, n\} を n 次の置換 (permutation) という。置換 \sigma, \eta \in S_n の合成 \eta \circ \sigma を置換の積という。
置換とは 1,2,3,\dots, n の入れ替えをしているイメージです(→線形代数(行列)における置換・奇置換・偶置換の最低限必要な知識)。
置換の定義をもとに,対称群・置換群の定義をしましょう。
定義(対称群・置換群)
n 次の置換全体の集合は,写像の合成に関して群となる。これを対称群 (symmetric group) といい, \color{red} S_n や \color{red}\mathfrak{S}_n などとかく。
対称群や,その部分群を置換群 (permutation group) という。
\mathfrak{S}_n の \mathfrak{S} はドイツ文字の「エス」です。本サイトでは,対称群は S_n という表記を用いることにします。
交代群の定義
交代群の定義には,もう少し知識が必要です。復習しましょう。
置換のうち,2つの元のみを入れ替えたもの \sigma(i)=j, \; \sigma(j)=i, \; \sigma(l)= l\,(l\ne i,j) を互換 (permutation) という。全ての置換 \sigma \in S_n は互換の積(合成)でかけることが知られている。
奇数個の互換の積でかける置換 \sigma を奇置換 (odd permutation) といい,偶数個の互換の積でかける置換 \sigma を偶置換 (even permutation) という。
この辺の話は,やはり線形代数(行列)における置換・奇置換・偶置換の最低限必要な知識で解説しています。この知識をもとに,交代群を定義します。
定義(交代群)
n 次の偶置換全体の集合は,対称群 S_n の部分群になる。これを交代群 (alternating group) といい, \color{red} A_n や \color{red} \mathfrak{A}_n とかく。
偶置換全体の集合は,対称群の部分群になります。実際,偶置換は偶数個の互換の積でかけますから,偶置換の積や逆置換も偶数個の互換の積,すなわち偶置換になりますね。よって部分群になります(→部分群の定義と判定方法~例4つと性質~)。
注意ですが,奇置換全体の集合は対称群の部分群にはなりません。奇置換の積は,(奇数+奇数)個の互換の積になり,これは偶置換になってしまいます。よって,積に対して閉じていないため,奇置換全体の集合は部分群ではありません。
置換の符号 \operatorname{sgn}(\sigma) を \sigma が偶置換のとき 1 ,奇置換なら -1 としましょう(→sign関数(sgn関数,符号関数)とは何か)。このとき,写像 \operatorname{sgn}\colon S_n \to \{\pm 1\} は準同型写像になります。ここで,
A_n= \operatorname{Ker}(\operatorname{sgn}) = \operatorname{sgn}^{-1} (1)
です。よって, A_n は置換の符号が 1 となる置換の集まりですね。特に, A_n は正規部分群になります(→正規部分群の定義と基本的な判定方法・具体例)。
【置換群】対称群・交代群の性質
対称群・交代群の大切な性質を2つ述べましょう。
対称群は有限群の母といわれることもあるかもしれませんが,それは,任意の有限群は対称群の部分群と考えることができるからです。
証明を記しておきましょう。
証明
G = \{g_1, g_2, \dots, g_n\} とする。 g_k\; (1\le k\le n) に対し, g_k g_j = g_{\rho_k (j)} とすると,これは置換 \rho_k \colon \{1,2,\dots, n\}\to \{1,2,\dots, n\} を定める。
ここで, f\colon G\ni g_k \mapsto \rho_k \in S_n は単射準同型であることを示そう。
- 単位元 e\in G に対し, eg_j = g_j より,f(e)= \operatorname{id} である
- g_k g_l \in G に対し, g_lg_k g_j = g_l g_{\rho_k(j)}=g_{\rho_l\rho_k(j)} より, f(g_lg_k) = \rho_l\rho_k = f(g_l)f(g_k)
- また上で, g_k = g_l^{-1},\, g_l = g_k^{-1} とすると, f(g^{-1} )= f(g)^{-1} もわかる
ので, f は準同型である。また, f(g) = \operatorname{id}\in S_n とすると,明らかに g=e なので単射でもある。よって, f は単射準同型である。
したがって準同型定理より, f\colon G \to f(G)\subset S_n は同型であり, G は S_n の部分群と同型ということになる。
証明終
次は,証明しませんが,大事な性質です。
定理(対称群・交代群の性質2)
n\ge 5 のとき S_n は可解群でない。
これは5次以上の代数方程式の解はべき根でかけないという「アーベル-ルフィニの定理」の根本になっています。可解群についても解説していませんが,大事な性質であるということを知っておくとよいでしょう。