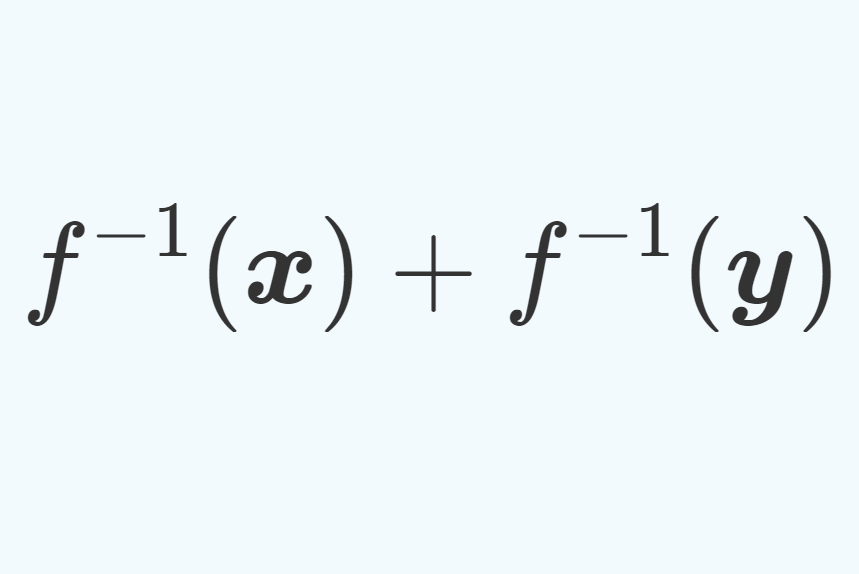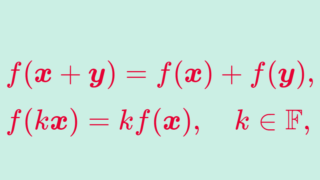PR

線形同型写像とベクトル空間の同型

線形代数学
用語・記号の定義大学教養
記事内に広告が含まれています。

線形同型写像とは，全単射な線形写像を指します。このような写像が存在する2つのベクトル空間は同型であるといい，全く同じものとして扱うことが可能です。

線形同型写像とベクトル空間の同型について，基本的なことをおさえましょう。

線形同型写像とベクトル空間の同型

まず定義の前に線形写像の復習をしておきましょう。線形写像とは以下をみたす写像です。

線形写像の復習
  • f(x+y)=f(x)+f(y) f(\boldsymbol{x}+\boldsymbol{y}) = f(\boldsymbol{x})+f(\boldsymbol{y})
  • f(kx)=kf(x) f(k\boldsymbol{x})=kf(\boldsymbol{x})

詳しくは以下で解説しています。

線形写像の定義・性質と具体例8つ
線形代数学ではとても大事な写像である，線形写像 (線型写像, linear map) について，その定義と，基本的な性質と具体例8個を確認していきましょう。ひとつずつ丁寧に，証明やコメントを添えながら進めていきます。
mathlandscape.com

これをもとに，定義を述べましょう。

定義（線形同型写像・ベクトル空間の同型）

V,W V,W をベクトル空間とし，f ⁣:V→W f\colon V\to W を線形写像とする。

f f が全単射であるとき，自動的に f−1 f^{-1} も線形写像になる(※)。このとき，f f を線形同型 (linear isomorphism) という。

ベクトル空間 V,W V,W の間に線形同型写像が存在するとき，V,W V,W は同型 (isomorphic) といい，V≃W \color{red}V\simeq W や V≅W\color{red} V\cong W などとかく。

ベクトル空間が同型であるとは，ベクトル空間として全く同じものと考えられるということです。数学においては，この「同型」という考え方は非常に大切です。

定義の※の部分の証明をしておきましょう。

定義の※の証明

V,W V,W を F \mathbb{F} 上のベクトル空間とする。

f ⁣:V→Wf\colon V\to W が同型であるとき，f−1 ⁣:W→V f^{-1}\colon W\to V が全単射であることは明らかであるから，f−1 f^{-1} が線形写像になることを示せばよい。

x,y∈W \boldsymbol{x},\boldsymbol{y}\in W とする。このとき，f∘f−1 f\circ f^{-1} は恒等写像で，f f は線形写像であるから，

x+y=f∘f−1(x+y),x+y=f∘f−1(x)+f∘f−1(y)=f(f−1(x)+f−1(y)) \begin{aligned}\boldsymbol{x}+\boldsymbol{y} &= f\circ f^{-1} ( \boldsymbol{x}+\boldsymbol{y} ) ,\\ \boldsymbol{x}+\boldsymbol{y} &= f\circ f^{-1} (\boldsymbol{x})+ f\circ f^{-1} (\boldsymbol{y}) \\ &= f(f^{-1} (\boldsymbol{x})+f^{-1}(\boldsymbol{y})) \end{aligned}


が成立する。よって，f∘f−1(x+y)=f(f−1(x)+f−1(y)) f\circ f^{-1} ( \boldsymbol{x}+\boldsymbol{y} ) = f(f^{-1} (\boldsymbol{x})+f^{-1}(\boldsymbol{y}) ) であり，両辺 f−1f^{-1} でうつすと，

f−1(x+y)=f−1(x)+f−1(y) f^{-1} ( \boldsymbol{x}+\boldsymbol{y} ) = f^{-1} (\boldsymbol{x})+f^{-1}(\boldsymbol{y})


となる。また，k∈F k\in \mathbb{F} とすると，

kx=f∘f−1(kx),kx=kf∘f−1(x)=f(kf−1(x))\begin{aligned} k\boldsymbol{x} &=f\circ f^{-1} (k\boldsymbol{x}), \\ k\boldsymbol{x} &= kf\circ f^{-1} (\boldsymbol{x}) = f(kf^{-1}(\boldsymbol{x})) \end{aligned}


なので，f∘f−1(kx)=f(kf−1(x)) f\circ f^{-1} (k\boldsymbol{x}) = f(kf^{-1}(\boldsymbol{x})) がわかる。両辺 f−1 f^{-1} でうつすと，

f−1(kx)=kf−1(x) f^{-1} (k\boldsymbol{x}) = kf^{-1}(\boldsymbol{x})


となる。ゆえに f−1 f^{-1} は線形写像である。

証明終

同型なベクトル空間の性質

同型なベクトル空間の性質を挙げましょう。

定理（同型なベクトル空間）

U,V,W U, V,W をベクトル空間とする。このとき，

  1. U≃V U\simeq V ならば dim⁡U=dim⁡V \dim U = \dim V (次元)。逆に，dim⁡U=dim⁡V<∞ \dim U =\dim V<\infty ならば U≃V U\simeq V である。
  2. U≃U U\simeq U (反射律)
  3. U≃V  ⟹  V≃U U \simeq V\implies V\simeq U (対称律)
  4. U≃V, V≃W  ⟹  U≃W U \simeq V,\, V\simeq W\implies U\simeq W (推移律)

特に，2-4.より「同型」という関係は同値関係である。

同値関係とは，まさに「同じものと思える関係」です。ベクトル空間が同型なら，それは全く同じものと思えます。

特に，1.の逆に以降より，V V を R \mathbb{R} 上の n<∞ n<\infty 次元ベクトル空間とすると，V≃Rn\color{red} V\simeq \mathbb{R}^n がわかります。

証明

1.の U≃V  ⟹  dim⁡U=dim⁡V U\simeq V\implies \dim U = \dim V について

f ⁣:U→V f\colon U\to V を同型写像とする。次元定理

dim⁡U=dim⁡Ker⁡f+rank⁡f \dim U = \dim\operatorname{Ker} f+ \operatorname{rank} f


について，いまの場合単射より Ker⁡f={0} \operatorname{Ker} f= \{\boldsymbol{0}\} (→線形写像が単射になる必要十分条件は核(Ker)が0になる証明)なのと，全射より rank⁡f=dim⁡Im⁡f=dim⁡V \operatorname{rank} f= \dim \operatorname{Im} f = \dim V が成り立つため，直ちに dim⁡U=dim⁡V \dim U = \dim V がわかる。

1.の dim⁡U=dim⁡V<∞  ⟹  U≃V \dim U=\dim V<\infty \implies U\simeq V について

dim⁡U=dim⁡V=n \dim U = \dim V = n とし，U,V U,V の基底をそれぞれ u1,…,un \boldsymbol{u_1},\dots, \boldsymbol{u_n}, v1,…,vn\boldsymbol{v_1},\dots, \boldsymbol{v_n} とする。このとき，

f(∑j=1nkjuj)=kjvj f\left(\sum_{j=1}^n k_j \boldsymbol{u_j}\right) = k_j \boldsymbol{v_j}


と定めると，これは線形同型写像である(演習問題とする)。よって U≃V U\simeq V である。

2. U≃U U\simeq U について

恒等写像は同型写像であるからわかる。

3. U≃V  ⟹  V≃U U \simeq V\implies V\simeq U について

f f が同型写像のとき，f−1 f^{-1} もそうであることは上の「※の証明」で示したとおりであるからわかる。

4. U≃V, V≃W  ⟹  U≃W U \simeq V,\, V\simeq W\implies U\simeq W について

f ⁣:U→V, g ⁣:V→W f\colon U\to V, \, g\colon V\to W が同型写像であるとき，g∘f ⁣:U→W g\circ f\colon U\to W が同型であることは簡単にわかるので，従う。

証明終

関連する記事

ベクトル空間・部分ベクトル空間の定義と具体例10個
ベクトル空間（線形空間，線型空間，vector space）は，簡単に理解できない概念の一つです。本記事では，まずベクトル空間と部分ベクトル空間の定義を述べ，様々な具体例を考えることで，少しでもベクトル空間を理解することを目指します。
mathlandscape.com
線形写像の定義・性質と具体例8つ
線形代数学ではとても大事な写像である，線形写像 (線型写像, linear map) について，その定義と，基本的な性質と具体例8個を確認していきましょう。ひとつずつ丁寧に，証明やコメントを添えながら進めていきます。
mathlandscape.com
同値関係の定義と重要な具体例5つ
同値関係 (equivalence relation) とは，二項関係～のうち，反射律・推移律・対称律をみたすものを言います。これについて，その定義と，重要な具体例5つを紹介しましょう。
mathlandscape.com