高校数学で扱う「はさみうちの原理 (挟み撃ちの原理; squeeze theorem)」は，大学数学におけるイプシロンエヌ論法・イプシロンデルタ論法を用いて厳密に証明されます。これについて紹介しましょう。
数列版のはさみうちの原理
まずは数列版の方の主張を述べ，証明しましょう。
数列版の定理の主張
定理（はさみうちの原理；数列版）
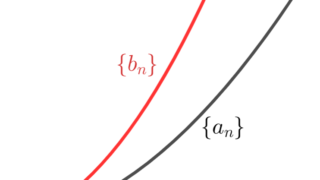
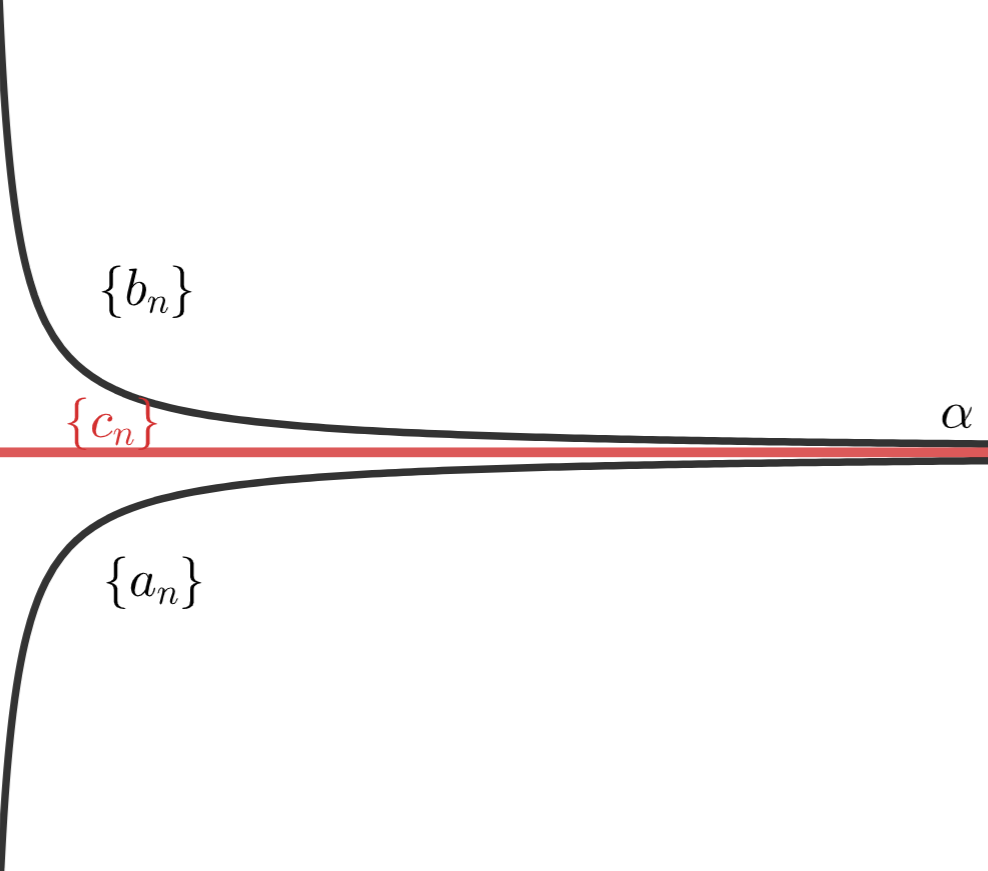
実数の数列 \{a_n\}, \{b_n\}, \{c_n\} において，
\color{red} a_n \le c_n \le b_n \,\, (n \ge 1 ) かつ \displaystyle \color{red}\lim_{n\to\infty} a_n = \lim_{n\to\infty} b_n = \alpha \in\mathbb{R} とする。
このとき，
が成立する。
証明には「イプシロンエヌ論法」を使います(→イプシロンエヌ論法をわかりやすく丁寧に～数列の極限の定義～ )。
数列版の証明
証明
\varepsilon > 0 とする。
\lim_{n\to\infty} a_n = \lim_{n\to\infty} b_n = \alpha であったから，それぞれある N_1, N_2 \ge 1 が存在して，
となる。ここで， N = \max\{N_1, N_2 \} としよう( N_1, N_2 のうち大きい方の値)。
すると， n \ge N のとき， |a_n - \alpha | < \varepsilon, \,\, |b_n - \alpha | < \varepsilon の両方が成り立つことになる。特に，
であるので，
が従う。すなわち， \lim_{n\to\infty} c_n = \alpha である。
証明終
関数版のはさみうちの原理
つづいて関数版の主張を述べ，証明しましょう。
関数版の定理の主張
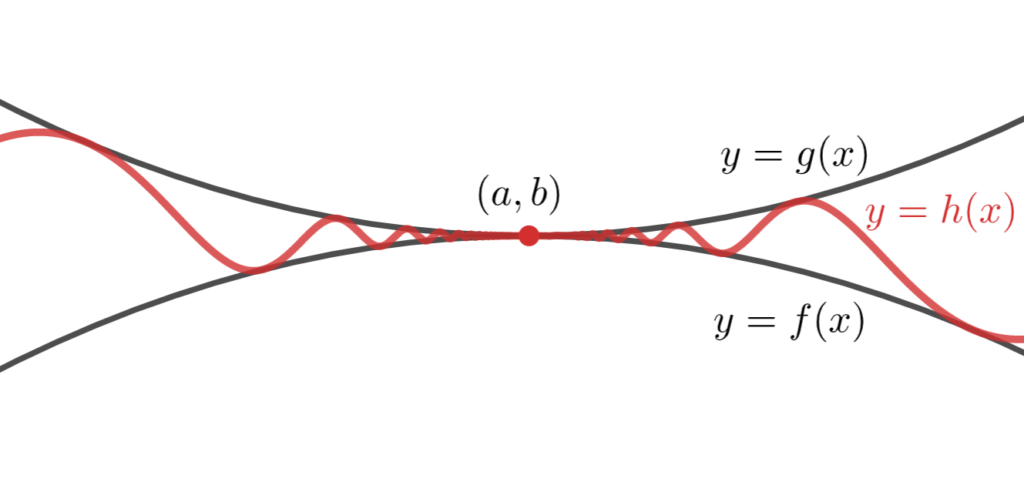
定理（はさみうちの原理；関数版）
f,g,h を -\infty \le a\le \infty の周りで定義されている実数値関数とし，
\displaystyle \color{red} f(x) \le h(x) \le g(x), \,\, \lim_{x\to a} f(x) = \lim_{x\to a} g(x) = b\in \mathbb{R} であるとする。
このとき，
が成立する。
証明には「イプシロンデルタ論法」を用います(→ イプシロンデルタ論法をわかりやすく丁寧に～関数の極限の定義～)。
関数版の証明
証明は数列版とほぼ同じです。
証明
1. - \infty < a < \infty のとき
\varepsilon> 0 とする。
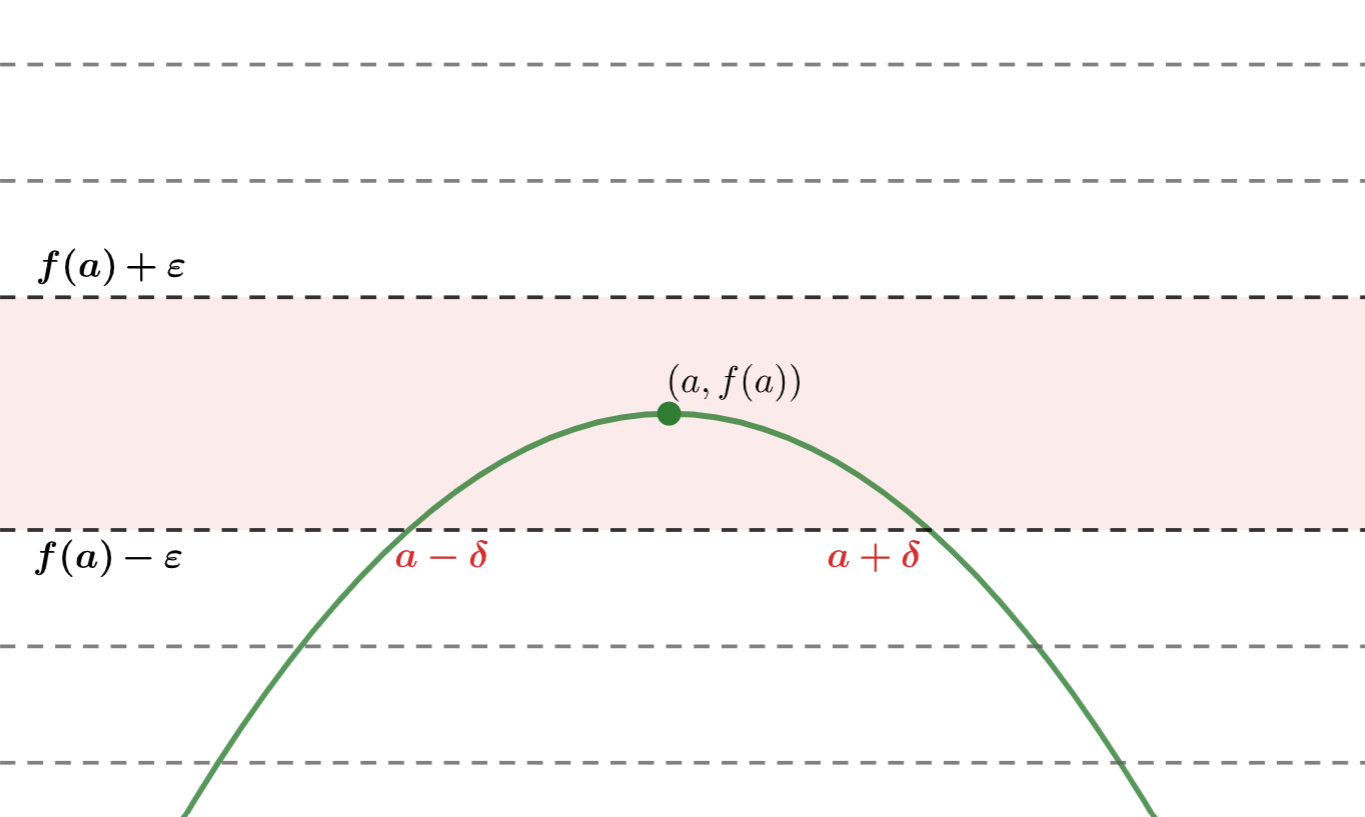
\lim_{x\to a} f(x) = \lim_{x\to a} g(x) = b であるから，それぞれある \delta_1, \delta_2 > 0 が存在して，
となる。ここで， \delta = \min\{ \delta_1, \delta_2\} としよう( \delta_1, \delta_2 のうち小さい方の値)。
すると， 0 < |x-a|<\delta のとき， |f(x) - b| < \varepsilon, \,\, |g(x) - b| < \varepsilon の両方が成立することになる。特に，
であるので，
が従う。すなわち \lim_{h\to a} h(x) = b である。
2. a=\pm\infty のとき
上の |x-a|< \delta_1,\,\, |x-a| < \delta_2, \,\,\delta=\min\{\delta_1, \delta_2 \} をそれぞれ x > K_1, \,\,x> K_2, \,\,K = \max\{K_1, K_2\} に変えると同様である。
証明終
似たような定理～追い出しの原理～
はさみうちの原理は収束する場合を扱いますが， \pm \infty に発散する場合を追い出しの原理といいます。主張だけ述べましょう。
定理（追い出しの原理；数列版）
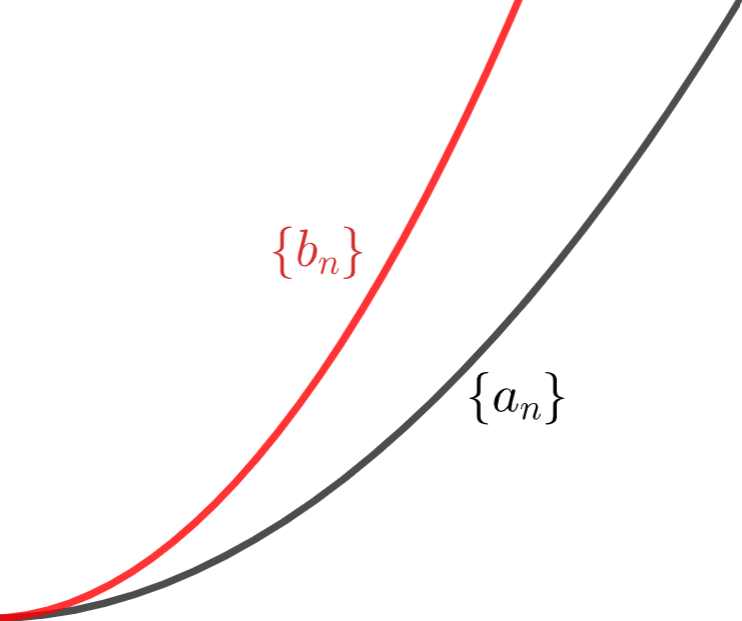
実数の数列 \{b_n\}, \{a_n\} が，
\color{red} a_n \le b_n \,\,(n\ge 1 ) かつ \color{red} \displaystyle\lim_{n\to\infty} a_n =\infty とする。
このとき，
が成立する。
定理（追い出しの原理；関数版）
f,g を -\infty \le a\le \infty の周りで定義されている実数値関数とし，
\displaystyle \color{red} f(x) \le g(x), \,\, \lim_{x\to a} f(x) = \infty であるとする。
このとき，
が成立する。
はさみうちの原理の証明が理解できれば，こちらの証明はほぼ自明かもしれませんが，以下の記事に証明があるため，適宜参照してみてください。
あとがき
大学数学においてこの原理を使う際，わざわざ「はさみうちの原理より」と断り書きを入れるようなことはありません。当たり前のように断りなく使います。
