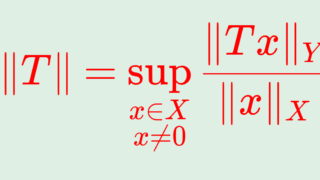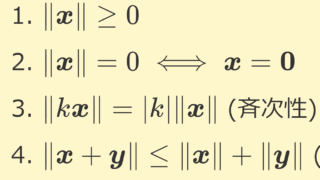バナッハ空間 (Banach space) とは,距離空間として完備なノルム空間のことを言います。これだけ聞いてもよく分からないかもしれません。バナッハ空間について,定義を詳しく紹介し,それから具体例5つと基本的性質を述べましょう。
バナッハ空間とは
もう少し,言葉を掘り下げておきましょう。まずはノルム空間とは何か復習しておきたいと思います。
\mathbb{C} 上ベクトル空間 X がノルム空間 (normed space) であるとは,以下のすべての条件をみたすノルム (norm) と呼ばれる関数 \|\cdot\|\colon X\to\R が定まっていることを言う。
- \lVert x\rVert \ge 0,\;x\in X
- \lVert {x}\rVert = 0\iff {x}={0}
- \lVert k{x}\rVert =| k|\lVert{x}\rVert,\; x\in X,k\in\mathbb{C}
- \lVert {x}+{y}\rVert\le \lVert{x}\rVert +\lVert {y}\rVert,\;x,y\in X (三角不等式)
詳しくはノルムとは~ノルム空間の定義と具体例~で解説しています。
ノルム空間は,二つのベクトルの間の距離を定めます。これにより,収束の概念が定義できます。ベクトルの列 \{x_n\}\subset X が x\in X に収束する (converge) とは,
\|x_n-x\|\xrightarrow{n\to\infty} 0
となることと定義します。これを単に x_n\to x\;(n\to\infty) とかきます。
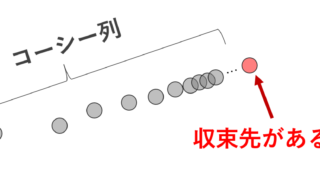
さて,収束の概念が考えられれば,「完備」までもうすぐです。完備とは,コーシー列が常に収束列になるような空間を指します。まずはコーシー列について,ノルム空間の記号を用いて定義を書いておきましょう。
ノルム空間 X 上の列 \{x_n\}\subset X がコーシー列 (Cauchy sequence) であるとは,
\lim_{n,m\to\infty} \|x_n-x_m\| =0
となることをいう。すなわち,任意の \varepsilon >0 に対して,ある N\ge 1 が存在し,
となることをいう。
要するに,\{x_n\} の番号 n が進めば進むほど,ベクトル同士の距離がどんどん近くなってくるということです。コーシー列が理解できれば,完備の定義はすぐそこです。
ノルム空間 X が完備 (complete) であるとは,任意のコーシー列が X 内における収束列になっていることである。
すなわち, 任意のコーシー列 \{x_n\} に対して,ある x\in X が存在して, x_n\to x\;(n\to\infty) とできることをいう。
より一般には,完備とは~実数の完備性・距離空間の完備性~で解説しています。
さて,完備という概念を復習しました。完備なノルム空間をバナッハ空間といったわけですね。ここまでついて来れれば,定義をきちんと理解したといえるでしょう。
バナッハ空間の具体例
さて,具体例を挙げていきましょう,
1. d次元ユークリッド空間 C^d, R^d
例1( d 次元ユークリッド空間 \mathbb{C}^d,\R^d ).
\mathbb{C} 上のベクトル空間 \mathbb{C}^d は x=(x_1,\dots, x_d)\in \mathbb{C}^d に対しノルム
\color{red}\|x\| = \sqrt{|x_1|^2+\dots + |x_d|^2}
によってバナッハ空間になる。 \R^d も同じである。
これがバナッハ空間になること(完備であること)を証明しておきましょう。
\mathbb{C}^d がバナッハ空間である証明
\{x_n = (x_n^{(1)},\dots, x_n^{(d)})\}_n\subset \mathbb{C}^d をコーシー列とする。整数 n,m\ge 1 と 1\le j\le d に対し,
|x_n^{(j)} -x_m^{(j)} |\le \|x_n-x_m\|
であるから, \{x_n^{(j)}\}_n\subset\mathbb{C} は \mathbb{C} 上のコーシー列である。\mathbb{C} は完備なので, \{x_n^{(j)}\}_n は収束先 x^{(j)}\in \mathbb{C} をもつ。 x=(x^{(1)},\dots, x^{(d)})\in\mathbb{C}^d とする。 x_n\xrightarrow{n\to\infty} x を示す。
\varepsilon>0 とする。 \mathbb{C} 上 x_n^{(j)}\xrightarrow{n\to\infty} x^{(j)} より,ある N_j \ge 1 が存在して,n\ge N_j\implies |x_n^{(j)}-x^{(j)} |<\varepsilon とできる。 N=\max\{ N_1,\dots, N_d\} とすると,
n\ge N\implies |x_n^{(j)}-x^{(j)} |<\varepsilon,\quad 1\le j\le d
とできる。よって n \ge N に対し,
であるから, x_n\xrightarrow{n\to\infty} x\in \mathbb{C}^d である。よって, \mathbb{C}^d は完備である。
証明終
コーシー列がちゃんと \mathbb{C}^d の中に収束元 x を持ったわけですから,完備であり,よってバナッハ空間です。
2. 有界閉区間上連続関数の空間 C[a,b]
例2(有界閉区間上連続関数の空間 C[a,b] ).
C[a,b] を [a,b] 上連続関数のなすベクトル空間とする。 f\in C[a,b] に対し,
\color{red}\|f\| = \sup_{a\le x\le b} |f(x)|
とすると, C[a,b] はバナッハ空間になる。
有界閉区間上の連続関数には,最大値が存在することが知られていますから, \|f\| = \max_{a\le x\le b} |f(x)| と書いても同じことです。
C[a,b] がバナッハ空間である証明
\{f_n\}\subset C[a,b] をコーシー列とする。すると,任意の \varepsilon >0 に対して,ある N\ge 1 が存在して, n,m\ge N に対し, \|f_n-f_m\| \le \varepsilon,すなわち
\begin{equation}|f_n(x)-f_m(x)|\le \varepsilon ,\quad a\le x\le b \end{equation}
とできる。 x\in [a,b] を固定すると, \{f_n(x)\} は \mathbb{C} 上のコーシー列であり,\mathbb{C} は完備であるから,ある f(x)\in\mathbb{C} が存在して, f_n(x)\xrightarrow{n\to\infty} f(x)\in\mathbb{C} とできる。
f(x) を f\colon [a,b]\to\mathbb{C} のように関数と見ると,関数列 \{ f_n\} は関数 f に各点収束するということになる。さらに, (1) 式で m\to\infty とすることにより,
|f_n(x)-f(x)|\le \varepsilon ,\quad a\le x\le b
となる。これは, \{f_n\} が f に一様収束することを意味し, \|f_n-f\|\xrightarrow{n\to\infty} 0 を意味する。
ここで,連続関数の一様収束先は連続関数であるから, f\in C[a,b] である。これにより,コーシー列 \{f_n\} は C[a,b] 内で収束先 f を持つから, C[a,b] は完備である。
証明終
一様収束の位相が入っている連続関数の空間ですね。
3. 無限遠が0に収束する連続関数の空間
例3( 無限遠が0に収束する連続関数の空間 C_0[a,b] ).
C_0(\R) を, \lim_{x\to\pm\infty} f(x)=0 となる連続関数 f\colon \R\to\mathbb{C} 全体の集合とする。 f\in C_0(\R) に対し,
\color{red}\|f\| = \sup_{ x\in \R} |f(x)|
とすると, C_0(\R) はバナッハ空間になる。
例2.は一様収束の話でしたが,今回も同じ一様収束の話で,証明は例2.と全く同じようにできます。さて,ここで,バナッハ空間の部分空間が必ずしもバナッハ空間にならない例を紹介しましょう。
C_c(\R) を, \{x\in\R\mid f(x)\ne 0\} が有界である連続関数全体の集合とします(専門的には,コンパクトな台を持つ連続関数といいます)。
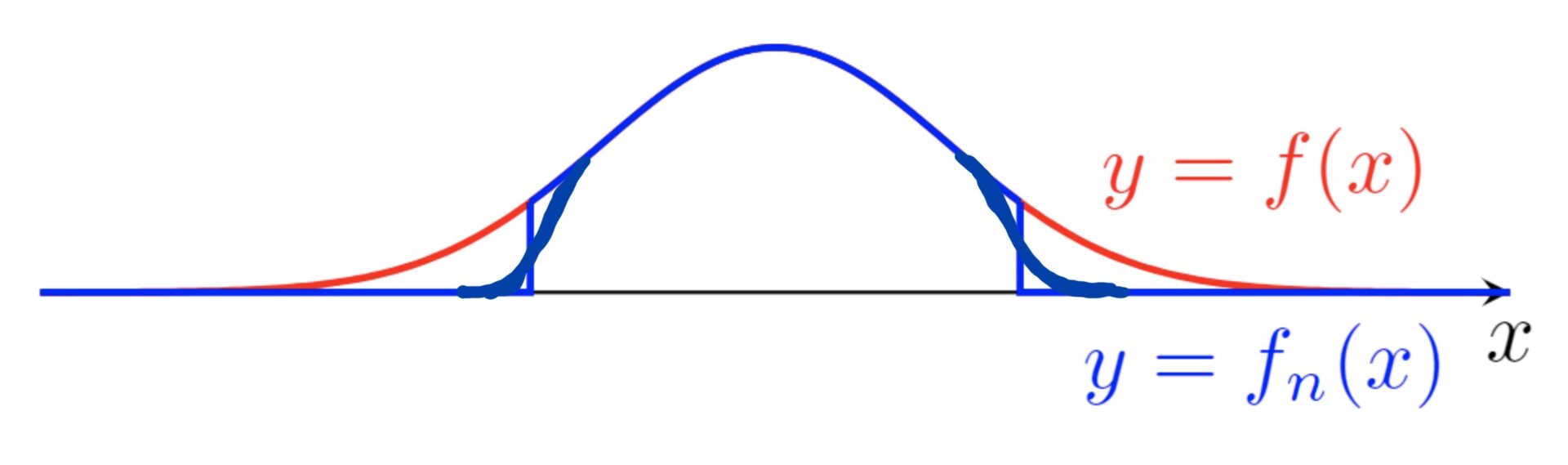
このとき, C_c(\R)\subset C_0(\R) であり, C_c(\R) は C_0(\R) の部分ノルム空間になります。ここで, f(x)=e^{-x^2} とし,さらに f_n(x) は e^{-x^2}1_{[-n,n]}(x) を「いい感じに」連続関数に補正したものとします(下図参照)( 1 は定義関数(特性関数))。
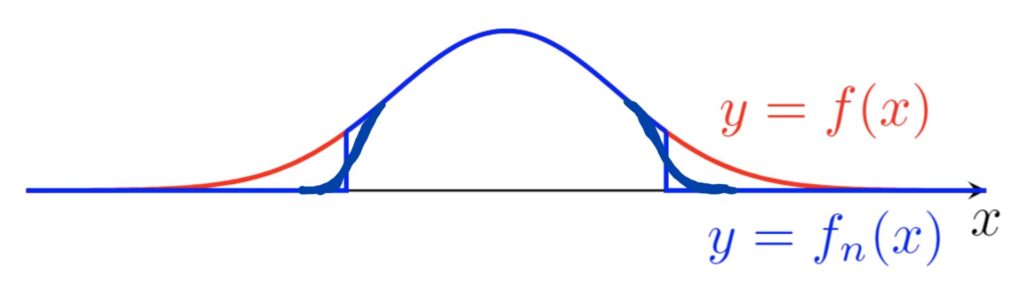
このとき, \{f_n\} \subset C_c(\mathbb{R}) であり,これはコーシー列になっています。実際, d(f_n, f_m) \le e^{-\min\{n, m\}^2} ですから,コーシー列です。さらに,
ですから, \{f_n\} は f に収束します。しかし, f\in C_0(\mathbb{R})\setminus C_c(\mathbb{R}) ですから,これは, \{f_n\} が C_c(\mathbb{R}) 上の関数に収束しないことを意味しており, C_c(\mathbb{R}) は完備ではありません。よってバナッハ空間ではありませんね。
4. 数列空間 l^p
例4(数列空間 \ell^p ).
1\le p<\infty とする。\ell^p を \sum_{n=1}^\infty |a_n|^p<\infty となる複素数列 \{a_n\} 全体のなすベクトル空間とする。このとき, a=\{a_n\}\in \ell^p に対し,
\color{red} \|a \|_p = \left( \sum_{n=1}^\infty |a_n|^p\right)^{1/p}
とすると, \ell^p はバナッハ空間になる。また, \ell^\infty を \max_{n\ge 1} |a_n|<\infty となる複素数列全体とすると,
と定めることで, \ell^\infty もバナッハ空間になる。
関数解析学でよく扱う空間の一つです。これがバナッハ空間になることは別の機会に証明しましょう。
5. 関数空間 L^p
例5(関数空間 L^p).
1\le p<\infty とする。L^p を \int_\R |f(x)|^p\, dx<\infty となる可測関数 f\colon \R\to \mathbb{C} 全体の集合(をa.e.の元で同一視したもの)とする。 このとき,f\in L^p に対し,
\color{red} \|f \|_p = \left( \int_\R \|f(x)|^p\, dx\right)^{1/p}
とすると, L^p はバナッハ空間になる。また, L^\infty を \operatorname{ess~sup} |f|<\infty となる可測関数 f\colon \R\to\mathbb{C} 全体の集合(をa.e.の元で同一視したもの)とすると,
と定めることで, L^\infty もバナッハ空間になる。ただし,ess sup は本質的上限を表す(→本質的上限・本質的下限(esssup,essinf)とは何か)。
これも,関数解析学でよく扱う空間です。これがバナッハ空間であることは別の機会に証明しましょう。
バナッハ空間の基本的性質
バナッハ空間の基本的性質をいくつか紹介します。
証明
有限次元ベクトル空間 X 上のノルムは全て同値である(→ノルムの同値性と有限次元空間のノルムは全て同値である証明)から,あるノルムに関してバナッハ空間であることを示せばよい。
\dim X=d とし, \{x_1,\dots, x_d\}\subset X を基底とする。 x=k_1x_1+\dots k_dx_d \quad(k_1,\dots, k_d\in\mathbb{C}) に対し,
\|x\| = \sqrt{|k_1|^2+\dots +|k_d|^2}
とすると,これは例1の \mathbb{C}^d と同じ議論により,バナッハ空間であることが示せる。よって,題意は示された。
証明終
無限次元ノルム空間が必ずしもバナッハ空間にならないことは,例3.の後に紹介しましたね。
定理2(バナッハ空間とその閉部分空間)
X をバナッハ空間とし, A\subset X をその閉部分空間(閉部分ベクトル空間)とする。このとき,
- A はバナッハ空間である。
- 商空間 X/A はバナッハ空間である。
1.については簡単に証明できます。今やってみましょう。
定理2-1の証明
\{x_n\}\subset A\subset X をコーシー列とすると, X の完備性より, x_n\to x\in X とできる。 A は閉なので, x\in A である。
特に A 上のコーシー列が A 上に収束先を持つので, A はバナッハ空間である。
証明終
なお,バナッハ空間の部分空間がバナッハ空間とは限らないことは,例3.でも確認したとおりです。バナッハ空間の部分空間がバナッハ空間であるための必要十分条件は,それが閉部分空間であることです。
2.についてはまたの機会に証明しましょう。
定理3(作用素の空間)
X をノルム空間, Y をバナッハ空間とする。このとき, X から Y への有界線形作用素全体の空間 \mathcal{L}(X,Y) はバナッハ空間である。
特に,ノルム空間 X に対して,その双対空間 X^* = B(X,\mathbb{C}) はバナッハ空間である。
定理3.の証明は以下で解説しています。
ヒルベルト空間
完備なノルム空間をバナッハ空間といいますが,完備な内積空間をヒルベルト空間 (Hilbert space) といいます。空間としては,以下のような関係です。

ヒルベルト空間については,以下で解説しています。