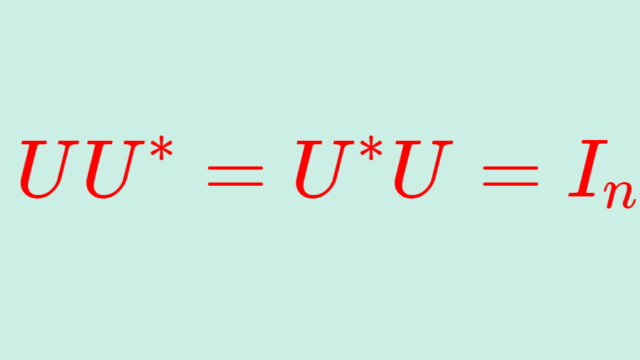 線形代数学
線形代数学 ユニタリ行列の定義と性質10個とその証明
ユニタリ行列 (unitary matrix) とは,UU^* =U^*U= I_nとなる正方行列 U を指します。これについて,定義と性質とその証明を行いましょう。
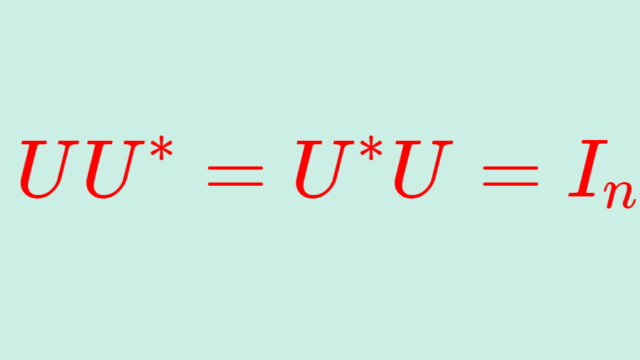 線形代数学
線形代数学 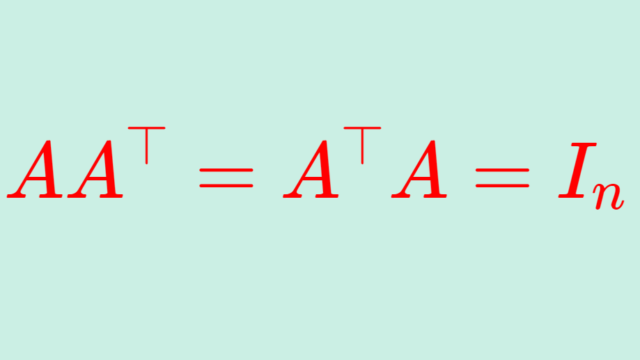 線形代数学
線形代数学  線形代数学
線形代数学 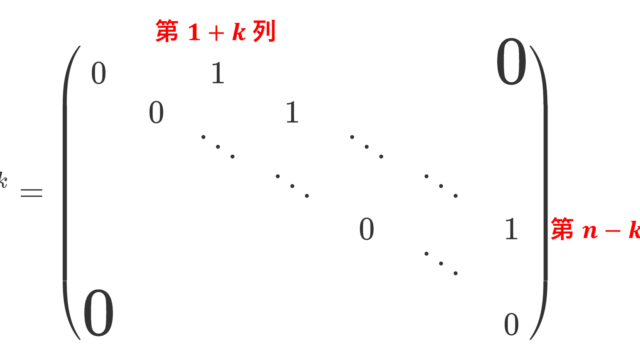 線形代数学
線形代数学 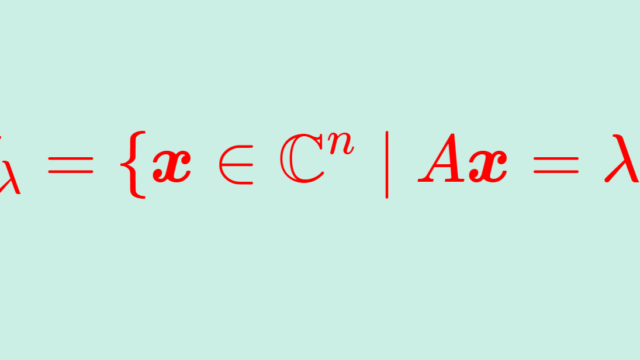 線形代数学
線形代数学 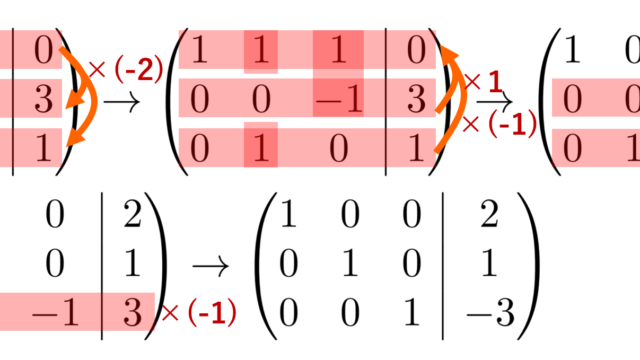 線形代数学
線形代数学 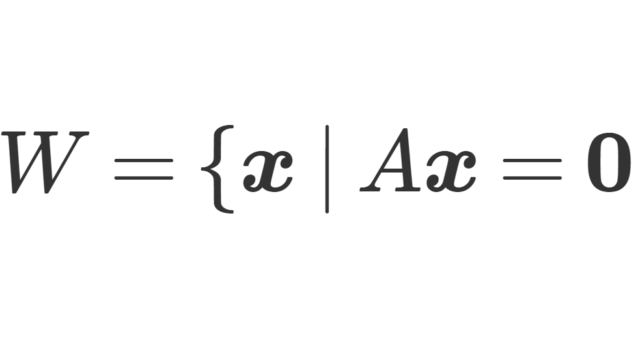 線形代数学
線形代数学 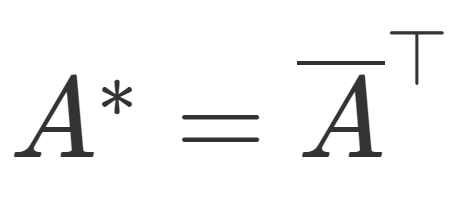 線形代数学
線形代数学 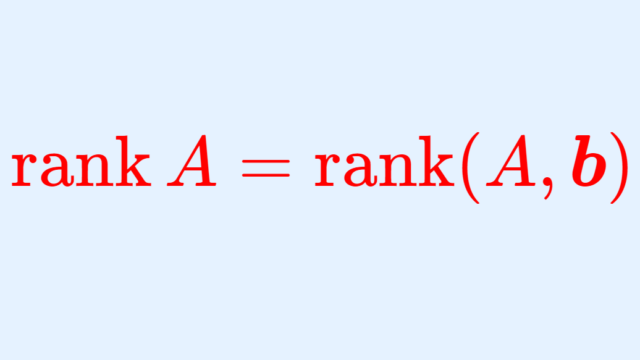 線形代数学
線形代数学 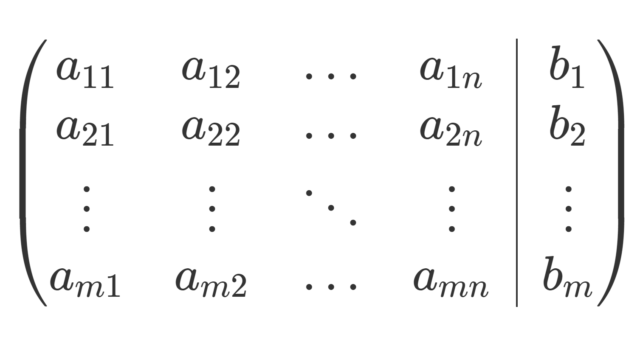 線形代数学
線形代数学