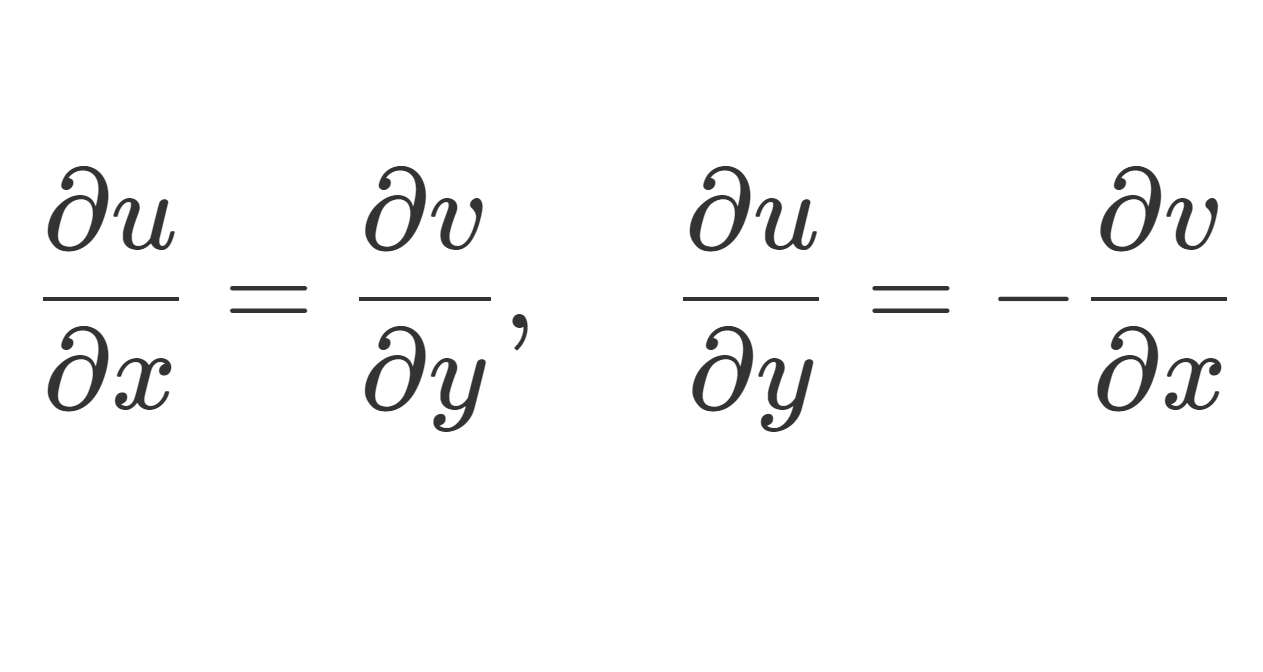複素関数論におけるコーシーリーマンの関係式とは, f(x+iy)=u(x,y)+iv(x,y) という式の
\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} ,\quad \frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}
という関係式を指します。 f が正則(複素微分可能)であるとき,この関係式が成り立つことが知られています。これについて,定理とその証明を述べましょう。
コーシーリーマンの関係式
f(z)=f(x+iy)=u(x,y)+iv(x,y)
のように,複素関数を,実多変数関数2つを使って表したとしましょう。具体的には,
とすることで, f\colon \mathbb{C}\to\mathbb{C} から u,v\colon \mathbb{R}^2\to \mathbb{R} を構成します。
f が複素関数として正則(すなわち微分可能)であれば,実2変数関数 u,v にはどのような関係が成り立つでしょうか。これについて述べたのが,コーシーリーマンの関係式です。定理を述べましょう。
定理(コーシーリーマンの関係式)
D\subset \mathbb{C} を開集合とする。 D 上の複素関数 f(z)=f(x+iy)=u(x,y)+iv(x,y) が D 上正則である必要十分条件は,
u,v\colon \mathbb{R}^2\to \mathbb{R} が D 上 C^1 級で,
が成立することである。
赤字の式を,コーシーリーマンの関係式 (Cauchy-Riemann equation) といいます。実数関数と見たときの偏微分です(→偏微分とは~定義と例題と図形的意味~)。
コーシーリーマンの関係式の例
証明の前に,一つだけ例を挙げましょう。 f(z)=z^3 はもちろん微分可能ですので,これを例にしましょう。
コーシーリーマンの関係式の例
f(z)=z^3 について,これは (x+iy)^3 = (x^3 + -3x y^2)+ i(3x^2y -y^3) なので,
\begin{aligned} u(x,y)&= x^3 + -3x y^2 , \\ v(x,y) &= 3x^2 y -y^3 \end{aligned}
である。これは,
なので,確かにコーシーリーマンの関係式が成立する。
コーシーリーマンの関係式の証明
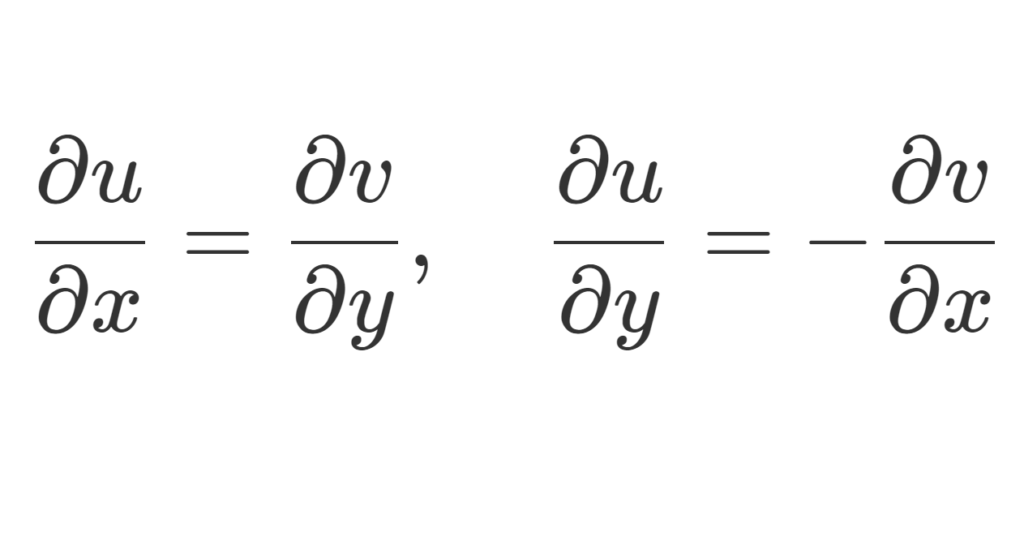
さて,証明に入りましょう。前半では,正則関数は,微分しても連続であることを使います。
正則 \implies コーシーリーマンの関係式について
f(z)=f(x+iy) は正則なので,特に2変数関数 f(x,y) とみて偏微分可能かつ偏導関数は連続で,特に u,v は C^1 級。加えて,
\begin{aligned} &\lim_{h\to 0} \frac{f(x+h,y)-f(x,y)}{h}\\ &= \lim_{h\to 0} \frac{f(x,y+h)-f(x,y)}{ih}\end{aligned}
でなければならないから, f_x= -if_y である。これの両辺の実部と虚部をそれぞれ比較することで,
が従う。
コーシーリーマンの関係式 \implies 正則について
u,v は C^1 級なので特に全微分可能で,ランダウの記号を用いると,コーシーリーマンの関係式の仮定より, A_1, A_2, x,y,h, k\in\mathbb{R} として,
\begin{aligned}&u(x+h,y+k)\\ &=u(x,y)+A_1h-A_2 k+o(\sqrt{h^2+k^2}), \\ &v(x+h,y+k)\\ &=v(x,y)+A_2h+A_1 k+o(\sqrt{h^2+k^2}), \end{aligned}
(h,k)\to (0,0). 上の2式のうち,2式目を i 倍してから両辺足し合わせると, A=A_1+iA_2 とおくことで,
すなわち, l=h+ik とおくことで,
これは, f が微分可能すなわち正則であることを意味する。
証明終
無事に証明できましたね。